20172328 2018-2019《Java软件结构与数据基础》第一周学习总结
2021-07-04 11:08
标签:问题 方法 移植 ali 需要 情况下 进度 ble 重要 高质量软件的特征 有关可靠性:可靠的软件很少发生故障,即使发生了故障,也可以将该故障的影响降到最低。 有关可维护性:软件系统必须经过细心设计、编码和文档说明,以便为开发人员、维护人员和用户的工作提供支持。 有关可移植性:Java的源代码被编译成了字节码,这是一种低级语言,他不是任何特定CPU的机器语言。字节码运行在Java虚拟上(JVM)。JVM是一种解释并执行字节码的软件。 有关运行效率:软件必须高效地使用诸如CPU时间和存储器之类的资源。 可用于给数列集排队的常用数据结构有有序列表、堆和散列表。 2.3增长函数的比较 方法调用的复杂度分析:与循环体的复杂度有关。 解决:其实这个问题是自己没有认真看书的后果。书本15页下有这样一段话: 在这种情况下,内层循环索引被初始化为外层循环索引的当前值。外层循环运行了n次,内层循环第一次被执行n次,第二次执行n-1次,等等……但是,记住,我们只对主项感兴趣,而忽视其他常数项或其他任何次要项。如果复杂度是线性的,则不管经过多少个元素,其阶次依旧是O(n),因此,上面的代码的复杂度为O(n^2)。 -20172301 莫听穿林打叶声,何妨吟啸且徐行。 20172328 2018-2019《Java软件结构与数据基础》第一周学习总结 标签:问题 方法 移植 ali 需要 情况下 进度 ble 重要 原文地址:https://www.cnblogs.com/LXY462283007/p/9612692.html20172328 2018-2019《Java软件结构与数据结构》第一周学习总结
概述 Generalization
本周学习了软件质量、数据结构以及算法分析的具体内容,主要依托于所用教材的第一章和第二章。
教材学习内容总结 A summary of textbook
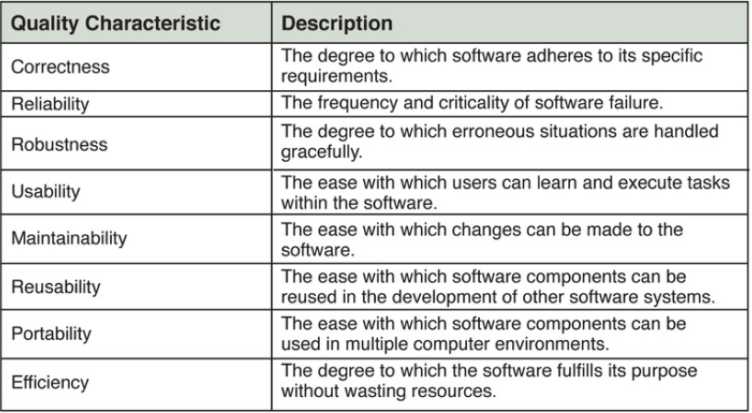
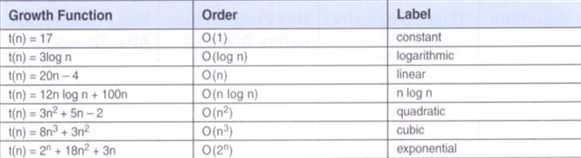
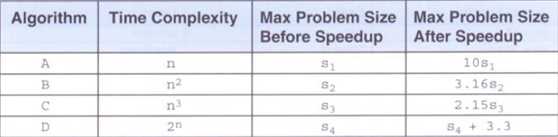
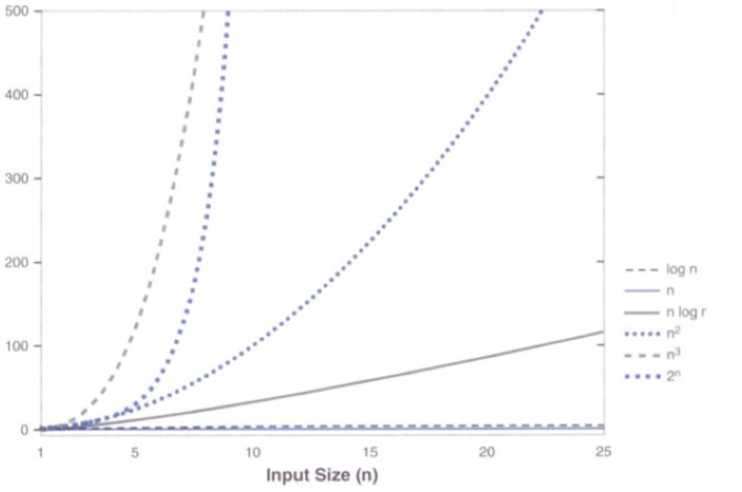
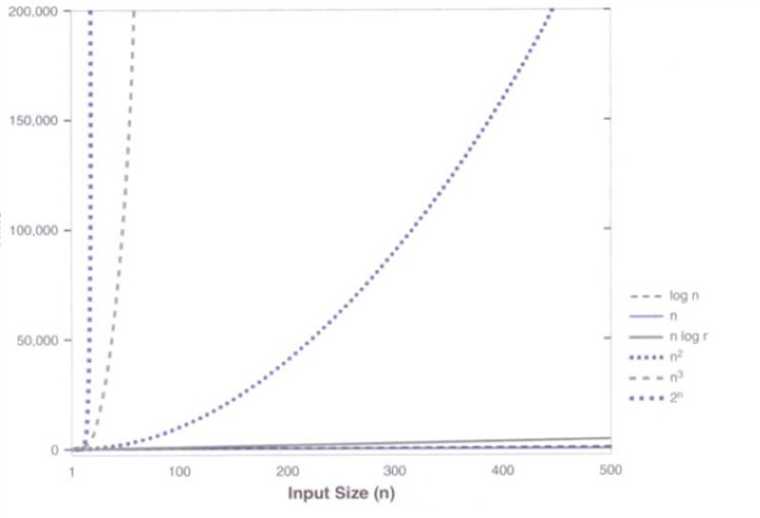
教材学习中的问题和解决过程 Problem and countermeasure
课后习题作答 Exercise
for(int count = 0 ; count
for(int count = 0 ; count
结对及互评 Group Estimate
-20172304点评模板:
其他(感悟、思考等,可选)Else
学习进度条 Learning List
代码行数(新增/累积)
博客量(新增/累积)
学习时间(新增/累积)
目标
5000行
30篇
400小时
第一周
0/0
1/1
8/8
参考资料 Reference
文章标题:20172328 2018-2019《Java软件结构与数据基础》第一周学习总结
文章链接:http://soscw.com/essay/101712.html