js math atan2
2021-07-15 11:04
标签:结果 w3c 范围 order 判断 运动 tab 坐标 通过 在双十二活动中,视觉要求实现一个鼠标跟随运动的的效果,就像“觉”的那个效果类似 其实原理很简单,看鼠标从哪个方向进的及从哪个方向出的,然后区块里绝对定位的浮层就可以根据鼠标方向 运动; 如:在鼠标进入事件中判断鼠标从左边进入区块那么定位层就从left:区块宽走到区块零,在鼠标离开事件中判断鼠标是从上边离开的那么定位层就从top:零走到负的区块高度就可以的。是不是很简单呢,但是有一个问题就是怎么判断方向?那么我们的atan2就隆重出场了。 看一下w3cshool上是怎么介绍atan2()的 atan2(x,y):返回-PI 到 PI 之间的值,是从 X 轴正向逆时针旋转到点 (x,y) 时经过的角度。 看维基网上的一张图: 那我们是不是计算出区块四个顶点的的atan2值,然和鼠标的atan2值比较确定范围看图: 是不由 CB>=RB&&CB CB>=LB&&CB 否则就在右边
js math atan2 标签:结果 w3c 范围 order 判断 运动 tab 坐标 通过 原文地址:http://www.cnblogs.com/yelongsan/p/7073507.html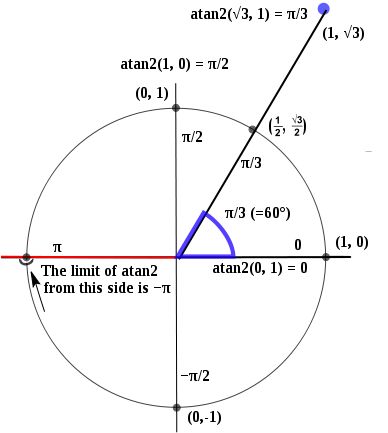
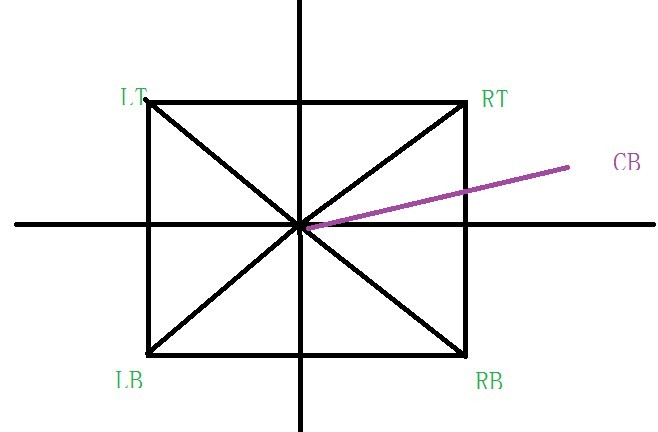
CB>=RT&&CB
我们可以使用正切操作将角度转变为斜率,那么怎样利用斜率来转换为角度呢?可以利用斜率的反正切函数将他转换为相应的角度.as中有两个函数可以计算反正切,我们来看一下.
1、as中Math.atan()
Math.atan()接受一个参数:用法如下:
angel=Math.atan(slope)
angel为一个角度的弧度值,slope为直线的斜率,是一个数字,这个数字可以是负的无穷大到正无穷大之间的任何一个值.
不过,利用他进行计算比较复杂.因为他的周期性,一个数字的反正切值不止一个.例如atan(-1)的值可能是45度,也可能是225度.这样就是他的周期性,对于正切函数来说,他的周期是180度,所以两个相差180度的角具有相同的正切和斜率:
tanθ=tan(θ+180)
然而,Math.atan()只能返回一个角度值,因此确定他的角度非常的复杂,而且,90度和270度的正切是无穷大,因为除数为零,我们也是比较难以处理的~!因此我们更多的会采用第二个函数.
2、Math.atan2()
Math.atan2()接受两个参数x和y,方法如下:
angel=Math.atan2(y,x)
x 指定点的 x 坐标的数字。
y 指定点的 y 坐标的数字。
计算出来的结果angel是一个弧度值,也可以表示相对直角三角形对角的角,其中 x 是临边边长,而 y 是对边边长。
下面我们来测试一下这两个函数:
x=Math.atan(1)//计算正切值为1的数字对应的弧度值
trace(x) //输出一个弧度值0.785398163397448
x=180*x/Math.PI//转换为角度值
trace(x) //输出45
x=Math.atan2(7,7)
trace(x)//输出0.785398163397448
x=180*x/Math.PI//转换为角度值
trace(x)//输出45
x=Math.atan2(7,-7)
trace(x)2.35619449019234
x=180*x/Math.PI//转换为角度值
trace(x)135
x=Math.atan2(-7,7)
trace(x)//输出-0.785398163397448
x=180*x/Math.PI//转换为角度值
trace(x)//输出-45
x=Math.atan2(-7,-7)
trace(x)//输出-2.35619449019234
x=180*x/Math.PI//转换为角度值
trace(x)//输出-135
//从这些测试可以看出,通过坐标系的自动调整,我们可以很自由的计算出处于不同象限的位置相对应的角度.
3、计算两点间连线的倾斜角.
这种方法非常的有用.
Math.atan2()函数返回点(x,y)和原点(0,0)之间直线的倾斜角.那么如何计算任意两点间直线的倾斜角呢?只需要将两点x,y坐标分别相减得到一个新的点(x2-x1,y2-y1).然后利用他求出角度就可以了.使用下面的一个转换可以实现计算出两点间连线的夹角.
Math.atan2(y2-y1,x2-x1)
不过这样我们得到的是一个弧度值,在一般情况下我们需要把它转换为一个角度.
下面我们用一段代码来测试一下这样的转换.
//测试,计算点(3,3)和(5,5)构成的连线的夹角
x=Math.atan2(5-3,5-3)
trace(x)//输出0.785398163397448
x=x*180/Math.PI//转换为角度
trace(x)//输出45