递推算法,AI衍生
2021-07-23 06:55
最近在刷leetcode算法题的时候,51题很有意思;
题目是这样的:
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q‘ 和 ‘.‘ 分别代表了皇后和空位。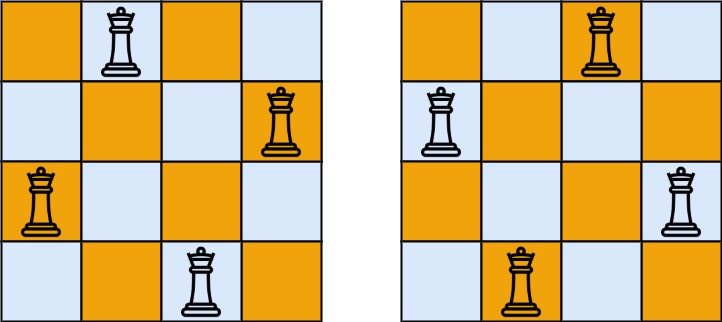
示例 1:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/n-queens
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这道题有意思地方在哪里,是它需要你算错所有的可能性;而不是其中的1种或者2种可能性;
看到这道题想起只有在游戏内做过的消除算法判定方案;《小游戏五子连珠消除解决方案》在这片文章中,我只是去验算内存中能消除的对象,也就是查找所有已经出现的对象进行判定;
这道题是让你从未知的开始,去填充数据,然后找出所有可能性;
题解1
第一遍读完题目的时候,我盲目的自以为然的写了一个算法;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
|
/** * @author: Troy.Chen(失足程序员, 15388152619)
* @version: 2021-07-08 10:53
**/
class Solution {
public Listint n) {
Listnew ArrayList();
List
for (int z = 0; z
for (int x = 0; x
boolean[][] action = action(ot, n, x, z);
if (action == null) {
continue;
}
Listnew ArrayList();
for (boolean[] booleans : action) {
String str = "";
for (boolean a : booleans) {
str += a ? "Q" : ".";
}
item.add(str);
}
ret.add(item);
}
}
return ret;
}
public boolean[][] action(List
boolean[][] tmp = new boolean[n][n];
tmp[startZ][startX] = true;
int qN = 1;
for (int z = 0; z
for (int x = 0; x
if (check(tmp, x, z)) {
tmp[z][x] = true;
qN++;
}
}
}
if (qN >= n) {
if (!ot.isEmpty()) {
for (boolean[][] tItem : ot) {
boolean check = true;
for (int z = 0; z
for (int x = 0; x
if (tmp[z][x]) {
if (tmp[z][x] != tItem[z][x]) {
check = false;
break;
}
}
}
if (!check) {
break;
}
}
if (check) {
return null;
}
}
}
ot.add(tmp);
return tmp;
} else {
return null;
}
}
public boolean check(boolean[][] tmp, int checkx, int checkz) {
/*检查横向*/
for (int x = 0; x
if (tmp[checkz][x]) {
return false;
}
}
/*检查纵向*/
for (int z = 0; z
if (tmp[z][checkx]) {
return false;
}
}
int tx;
int tz;
{
/*从左到右,从上到下*/
tx = checkx;
tz = checkz;
while (true) {
if (tmp[tz][tx]) {
return false;
}
tx--;
tz--;
if (tx
break;
}
}
tx = checkx;
tz = checkz;
while (true) {
if (tmp[tz][tx]) {
return false;
}
tx++;
tz++;
if (tx >= tmp.length || tz >= tmp.length) {
break;
}
}
}
{
/*从右到左,从上到下*/
tx = checkx;
tz = checkz;
while (true) {
if (tmp[tz][tx]) {
return false;
}
tx++;
tz--;
if (tx >= tmp.length || tz
break;
}
}
tx = checkx;
tz = checkz;
while (true) {
if (tmp[tz][tx]) {
return false;
}
tx--;
tz++;
if (tx
break;
}
}
}
return true;
}
}
|
这个写法,是我脑袋里的第一想法,代码怎么理解呢;
就是说我从第一个位置开始去摆放皇后,然后依次去递推其他格子皇后摆放位置,然后查询皇后数量是否符合提议;自己测试了即便就感觉对了,在leetcode提交代码
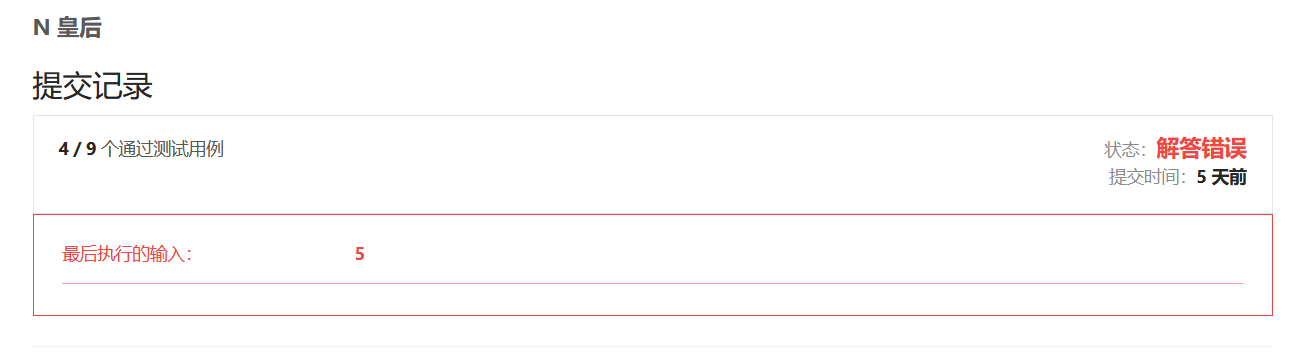
提交代码过后啪啪打脸了,失败了
查看执行输出,当输入n=6的时候;
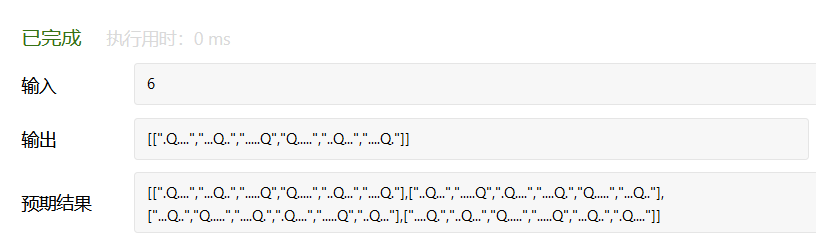
leetcode的输出结果是有4种可能性,但是我输出可能性只有1种;
对比之前五子棋消除方案来讲;check代码无疑是没有问题的,起码我在对于纵向横向,斜45度检查方案是没问题的;能保住输出是符合要求的,
那么问题就在于查找可能性代码;我们能找出符合条件的可能性,只是没有办法去找出所有的可能性
仔细分析了一下,不难看出完整的循环一次,得出的结果其实是固定;
怎么理解呢,因为每一次for循环数值都是从0开始推导;那么找到第一个符合条件的格子就落子了,所以得到的结果总是一致的;
既然我们需要算出所有组合;
那么我们能有什么样的方式去完成这个组合求解呢?
题解2
思考了良久;既然正常的循环其实无法查找每一种可能性,只能放弃正常循环;
思考了一下能不能按照当前行,每一个格子,依次往下逐行去扫描每一种可能性;
如果我们要这样去逐行扫描,我们就得在初始化棋盘格子到时候摆放上,上一行的情况才能去推算出当前行能在那些地方摆放;
当前行的递推的时候也是按照第一个格子到最后一个格子去验算能摆放的格子,然后查找到能摆放的格子,就把现在的快照数据提交给下一行进行推算;
这样的做法就是,当第一行开始判断是,第一个格子肯定能摆放棋子对吧,然后把第一个格子摆放上棋子过后,把棋盘直接推给第二行,
第二行拿到棋盘过后,去查找能摆放的格子,每查找到能摆放的格子就把棋盘拷贝一次副本,然后设置当前查找的格子落子,然后把副本棋盘传递给下一行;
这样依次类推,如果能达到最后一行,并且找到适合的格子,那么就是一种可能性,
我们在递推的同时,每一次都会记录自己的进度,再次往下递推;
这么说可能有些抽象;来看一下图
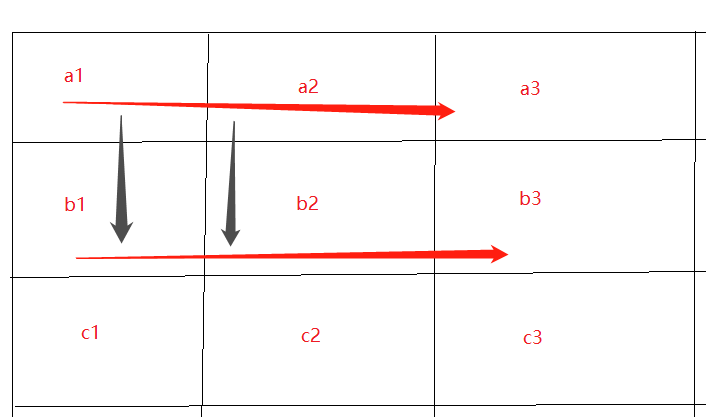
我们的递推过程就是,从a1开始,每一次找到合适的格子就把棋盘拷贝一次,传递给下一行(b),然后b开始从第一个格子开始递推,找到符合规则的格子就再一次拷贝棋盘传递给C;
这样的话,就是完完整的逐行扫描了,所有的肯能行;
来看一下带实现

/**
* @author: Troy.Chen(失足程序员, 15388152619)
* @version: 2021-07-08 10:53
**/
class Solution {
public List> solveNQueens(int n) {
List> ret = new ArrayList();
List ot = new ArrayList();
boolean[][] tmp = new boolean[n][n];
check(ot, tmp, 0, 0);
for (boolean[][] a : ot) {
ret.add(convert(a));
}
return ret;
}
/*按照规定转化字符串*/
public List convert(boolean[][] tmp) {
List item = new ArrayList();
for (boolean[] booleans : tmp) {
String str = "";
for (boolean a : booleans) {
str += a ? "Q" : ".";
}
item.add(str);
}
return item;
}
public void check(List ot, boolean[][] tmp, int checkx, int checkz) {
for (int x = checkx; x = tmp.length || tz >= tmp.length) {
break;
}
}
}
{
/*从右到左,从上到下*/
tx = checkx;
tz = checkz;
while (true) {
if (tmp[tz][tx]) {
return false;
}
tx++;
tz--;
if (tx >= tmp.length || tz = tmp.length) {
break;
}
}
}
return true;
}
}

再次提交代码;
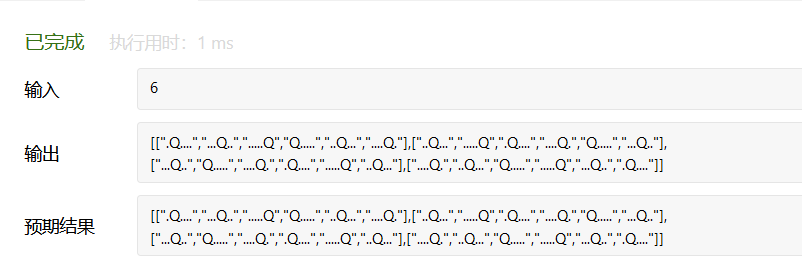
代码执行通过了,得到的结论也是一样的了;
但是不幸的是我的代码只击败了8%的用户,希望得到各位园友性能更高效的算法;
总结
这样的递推方式,其实可以实现像五子棋AI算法;通过落子情况去递推在哪里下子可以得到五个棋子在一条线上;
只是递推开上时棋盘已经定下了落子情况;从当前的落子情况去递推他的可能性;
递推算法,AI衍生
标签:总结 性能 pac 无法 lis ddl 判断 add 著作权
原文地址:https://www.cnblogs.com/wl-blog/p/15014140.html
上一篇:C#简单生成缩略图的方法
下一篇:【1】排行榜算法设计