八皇后问题遗传算法实现(python版)
2020-12-17 16:35
标签:code 集合 count 框架 pap 算法实现 __name__ 下一代 last 八皇后问题的遗传算法实现过程详解 1、八皇后问题描述 基本遗传算法给出了基本框架, 针对求解的问题不同, 遗传算法在相应的计算步骤中有不同的设计。本文针对八皇后问题, 设计了相应的编码,适应度计算方法,交叉和变异操作。 3、用遗传算法求解八皇后问题实现过程详解 3.1 编码 3.2 个体评价 3.3 选择 3.4 交叉 经典的单点, 多点等交叉因染色体中不能出现重复的基因值,在该问题中不适用。本文使用部分匹配交叉,具体操作如下: 如:染色体a:01y24y3675; 染色体b:12y30y4576; 两个y 之间的基因段称为中间段, 记录其对应关系2-3,4-0; 形成染色体a‘:01y30y3675;染色体b‘: 12y24y4576; 3) 利用对应关系,对染色体a‘, b‘ 中间段外的基因进行交换, 形成 染色体a‘‘: 41y30y2675; 染色体b‘‘: 13y24y0576; 交叉完成。 3.5 变异 本文采取随机地选取染色体内的两个基因进行交换来实现。 例如随机选取的是 3.6 终止策略 4、总结 八皇后问题遗传算法实现(python版) 标签:code 集合 count 框架 pap 算法实现 __name__ 下一代 last 原文地址:https://www.cnblogs.com/liweikuan/p/14103482.html
19 世纪著名的数学家Gauss 在1850 年提出八皇后问题后, 该问题成为各类语言程序设计的经典题目。八皇后问题要求在8×8 格的国际象棋上摆放八个皇后,使横、竖、斜方向上都不能有两个及两个以上皇后在同一条直线上, 问题也可以推广到N 个皇后。穷举法在问题规模不大的情况下还可适用,回溯法是求解此问题的经典算法。但N 皇后问题是个NP 难问题, 随着皇后数目的增多, 求解复杂度激增, 就需利用非常规的技术求
解。遗传算法在求解一些NP 完全问题上得到了广泛地应用,本文用遗传算法求解八皇后问题,给出详细的实现过程。
2、基本遗传算法求解过程
基本遗传以初始种群为基点, 经过选择、交叉、变异操作生成新的种群,如此更新种群直到满足终止条件。其计算步骤如下:
(1) 将问题空间转换为遗传空间, 也就是编
码;
(2)随机生成P 个染色体作为初始种群;
(3)染色体评价,也就是按确定的适应度函数
计算各个染色体的适应度;
(4)根据染色体适应度,按选择算子进行染色
体的选择;
(5)按交叉概率进行交叉操作;
(6)按变异概率进行变异操作;
(7)返回(4)形成新的种群,继续迭代,直到满足终止条件。
遗传算法中传统的编码是二进制编码, 本文采用多值编码。染色体长度取决于皇后的个数。染色体中每个基因所处的位置表示其在棋谱中所在的行数, 基因值表示其所在的列数。如染色体40752613 表示:从0 开始数,第0 个4 表示在第零行的皇后在第4 列, 第1 个0 表示第一行的皇后在第0 列,以此类推。八皇后问题中皇后不能处于同行同列, 意味着染色体中0~7 的基因取值不能出现重复。
染色体通常表示了问题的可行解, 对可行解进行遗传操作寻找最优解。但在八皇后问题中,染色体仅仅体现同行同列中未出现互攻, 在对角线上是否出现互攻还未做考虑。在对皇后的位置做比较的时候, 可以对两个棋子的行数差与列数差进行对比, 实现了互攻次数的统计。公式为:|绝对值((y2-y1)/(x2-x1)) |=1。公式中(x1,y1),(x2,y2)分别表示两个皇后所在的位置,即所在的行数和列数。当两个皇后的行数差与列数差比值的绝对值为1 的时候,两皇后在同一对角线上,即出现了互攻。每个染色体内的互攻次数为Value,初始值设为0;第0 行与1~7 行进行比较, 每出现一次互攻则Value 的值增加1;第1 行与2~7 行进行比较,以此类推来计算Value 值。当Value 为0 表示没有发生互攻,此染色体就是其中的一个可行解。当Value 不为0则进行适应度的计算。一般来说, 适应度越大越
好,而互攻次数为越小越好,所以可以将适应度的计算函数设置为:F=28-Value。
选择使用的是经典的赌轮选择方法, 与基本遗传算法的实现无特别之处,此处不赘述。
1)在染色体中随机选取两个点标记为y,
2)对染色体a,b 的中间段进行交换,
采用多值编码后, 变异操作并不能通过简单的0,1 反转实现。
6 和1 两个基因,那么
变异前染色体: 7 (6) 5 4 3 2 (1) 0
变异后染色体: 7 (1) 5 4 3 2 (6) 0
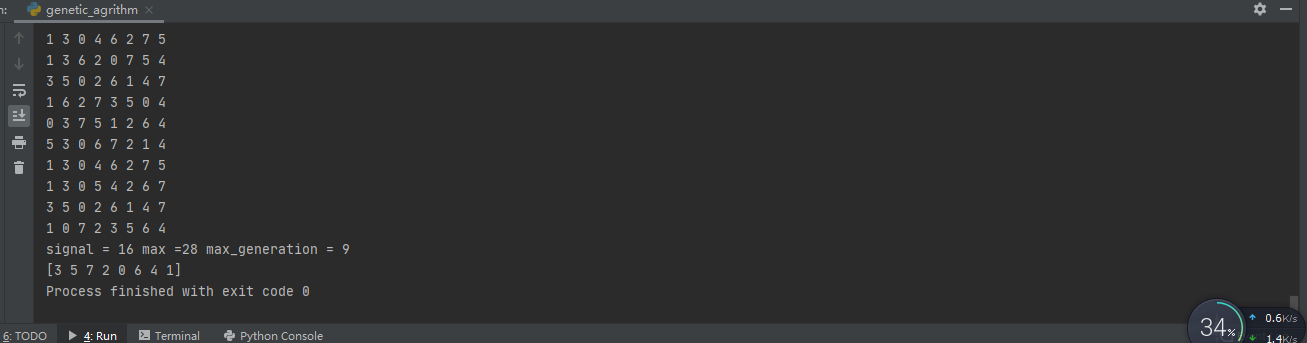
本文采用的终止策略为: 当群体中出现染色体的适应值为0 时, 即表示算法搜索到了一个可行解,终止算法。若算法运行设置的代数还未找到可行解,同样终止程序运行。
本文详细介绍了用遗传算法求解八皇后问题的求解过程, 但要注意的是这只是其中的一种编码,交叉,变异等操作设计方法,还有许多其他的方法可以选择。对于各操作采取不同设计方案的遗传算法,其算法性能值得比较讨论。 1 #
2 # 遗传算法(八皇后问题)
3 #
4 import random
5 import numpy
6
7
8 N=8 #皇后数
9 Cluster_size=12 #默认种群大小
10 LASTG=100 #/*终止后代*/
11 MRATE=0.8 #/*突变的概率*/
12 array=numpy.zeros((Cluster_size,N)).astype(int) #染色体集合
13 narray=numpy.zeros((Cluster_size * 2,N)).astype(int) #下一代染色体集合
14 _array=numpy.zeros((Cluster_size,N)).astype(int)#array数组的副本
15 values=numpy.zeros(Cluster_size).astype(int) #评估数组
16 max_array=numpy.zeros(N).astype(int) #保存最佳数组
17 generation = 0 #记录代数
18 signal = -1 # 信号
19 max = -1 # 记录当前最优值
20 max_generation = -1 #记录当前最优值代数
21
22
23
24 class Struct:
25 key = numpy.zeros(N).astype(int)
26 values = numpy.zeros(N).astype(int)
27
28
29 rember=Struct()
30
31
32 def rndn(l):
33 rndno =random.randint(0,l-1)
34 return rndno
35
36
37 def copy_array():
38 for i in range(Cluster_size):
39 for j in range(N):
40 _array[i][j]=array[i][j]
41
42
43 def output_copy_array():
44 for i in range(Cluster_size):
45 for j in range(N):
46 print(_array[i][j],end=" ")
47 print()
48
49
50 def the_answer(values,size):
51 for i in range(size):
52 if values[i]==28:
53 return i
54 return -1
55
56
57 def judge(a,n):
58 value = -1
59 for i in range(n):
60 value = a[i]
61 j=i+1
62 while jn:
63 if(value==a[j]):
64 return 0
65 j+=1
66 return 1
67
68
69
70 def count_collidecount():
71 value=0
72 global signal
73 for i in range(Cluster_size):
74 for j in range(N):
75 x1=j
76 y1=array[i][j]
77 m=j+1
78 while mN:
79 x2=m
80 y2=array[i][m]
81 if (abs((y2-y1)/(x2-x1))==1):
82 value+=1
83 m+=1
84 values[i]=28-value
85 value=0
86 signal= the_answer(values,Cluster_size)
87
88
89
90 def count_generation_collidecount(values,cluster_size):
91 value=0
92 for i in range(cluster_size):
93 for j in range(N):
94 x1=j
95 y1=narray[i][j]
96 m=j+1
97 while mN:
98 x2=m
99 y2=narray[i][m]
100 if(abs((y2 - y1) / (x2 - x1))==1):
101 value+=1
102 m+=1
103 values[i]=28-value
104 value=0
105
106
107 # /************************/
108 # /* selectp()函数 */
109 # /* 父代的选择 */
110 # /************************/
111 def selectp(roulette,totalfitness):
112 acc=0
113 ball=rndn(totalfitness)
114 for i in range(Cluster_size):
115 acc+=roulette[i]
116 if (acc>ball):
117 break
118 return i
119
120
121 def takeoutrepeat( position):
122 signal=True
123 for i in range(N):
124 value = narray[position*2][i]
125 j=i+1
126 while jN:
127 if (narray[position*2][j]==value):
128 # print("there have reapt number: "+str(position*2))
129 signal=False
130 j+=1
131 for i in range(N):
132 value=narray[position*2+1][i]
133 j=i+1
134 while jN:
135 if (narray[position*2+1][j]==value):
136 # print("there have reapt number: "+str(position*2+1))
137 signal=False
138 j+=1
139 return signal
140
141
142
143
144 def judge_reapt(c, cluster):
145 value =0
146 arraysEqual =True
147 i=0
148 for j in range(cluster):
149 while (arraysEqual and iN):
150 if (narray[c][i] !=_array[j][i]):
151 arraysEqual=False
152 i+=1
153 if(arraysEqual):
154 value+=1
155 else:
156 arraysEqual=True
157 i=0
158
159 if(value>0):
160 return False
161 else:
162 return True
163
164
165
166
167 # /************************/
168 # /* selection()函数 */
169 # /* 选择下一代 */
170 # /************************
171
172 def selection():
173 global signal
174 global max_generation
175 global max
176 totalfitness=0
177 roulette=numpy.zeros(Cluster_size*2).astype(int)
178 acc=0
179 for i in range(Cluster_size):
180 totalfitness=0
181 count_generation_collidecount(roulette,Cluster_size*2)
182 c=0
183 while c