Luogu P3631 [APIO2011]方格染色
2020-12-26 00:27
标签:continue cst tchar string strong lang 不同 turn 因此 对于这道题,我们从题目里可以知道,蓝色代表的方块为0,红色代表的方块为1。按照题目要求,如果换一种说法,那就是对于一个2*2的方格,其中1的个数必定有奇数个,这样的话,每个方格里的所 有数的异或和必定为1(0^0=0 , 1^0=1 , 1^1=0)。那么对于每一个格子\(a(i,j)\),都有:a(i,j)^a(i+1,j)^a(i,j+1)^a(i+1,j+1)=1 我们钦定S(i , j)为每一个以点(i , j)为右下角的方格的异或和。然后把范围扩大,设想对于一个i*j的方格,它的异或和会是什么呢?(这个部分需要自己推一下,时间关系我就不给例子了) 我们多举几个例子,就可以发现对于任意一个以点(i , j)为右下角的矩阵,它的区域内所有可能的22的方格的异或和再异或起来,得到的就是以(i , j)为右下角的矩阵中包括的所有22矩阵的异 或和的异或和。而这个异或和,根据a^a=0的规定,这个矩阵的S(i , j)仅仅与点(1 , 1)、(i , 1)、(1 , j)、(i , j)有关。 再以此类推,我们就可以发现对于任意一个点,它的值只与(1 , 1)、(i , 1)、(j , 1)这几个点有关。因此我们就可以知道,只要我们明确了表格中第一列和第一行的内容,那表格中其他点 的内容也就是唯一的。 因此,对于a(1 , 1)^a(i , 1)^(1 , j)^a(i , j),当i,j均为偶数时值为1(此时\((i-1) \times (j-1)\)为奇数,对于S函数的异或前缀和为1),否则为0(此时(i-1)*(j-1)为偶数,对于 S函数的异或前缀和为0)。即为a(1 , 1)^a(i , 1)^(1 , j)^a(i , j)=0/1(这里0/1表示值为0或者1)。 这样的话,我们可以考虑枚举a(1 , 1)的值,根据a(i , j)和a(1 , 1)的异同关系(就是对于上一段中说的i , j的奇偶性的问题),就可以确定a(i , 1)和a(1 , j)的异同关系, 即a(i , 1)^a(1 , j)=0/1^0/1^a(i , j)。 那么到现在我们还没有提到过关于并查集的一个字(而这又是一道并查集的题目)。由于我们可以通过枚举a(1 , 1)确定出a(i , 1)和a(j , 1)的异同关系,我们就应该有所启发。 考虑一下食物链那道题。同样都是维护不同的集合,维护集合的关系,这样想这两个题就是极其类似的。我们使用并查集维护有关系的点a(i , 1)和a(j , 1)的异同关系,将他们之间连边。 最后考虑有多少个集合,答案即为2的集合数量减1次方。有人可能会有疑问,为什么不是2的集合个数次方呢?这是因为(1 , 1)这个点自己就是一个集合,但是对答案并没有贡献,所以要减一。 Code Luogu P3631 [APIO2011]方格染色 标签:continue cst tchar string strong lang 不同 turn 因此 原文地址:https://www.cnblogs.com/ShadowFlowhyc/p/13381923.html
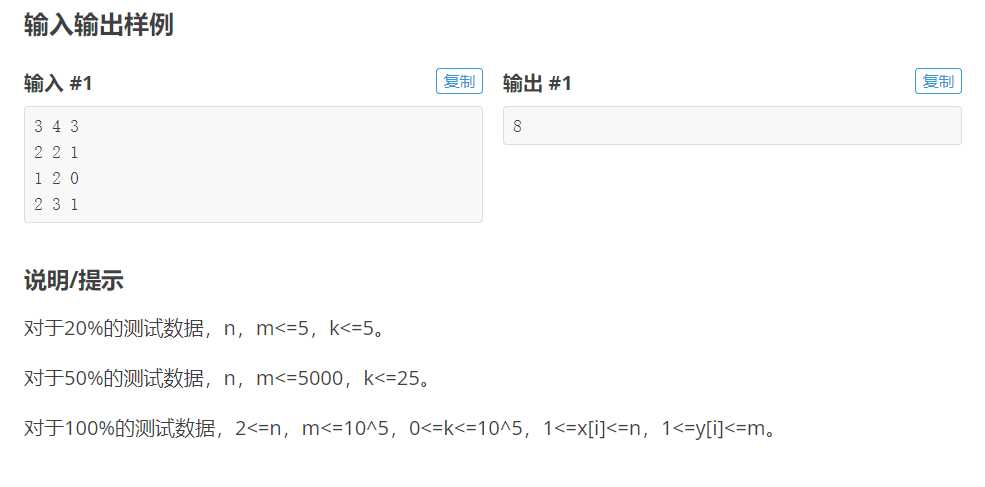
思路
#include
上一篇:Winlogbeat之安装