排序(二)
2021-01-15 00:12
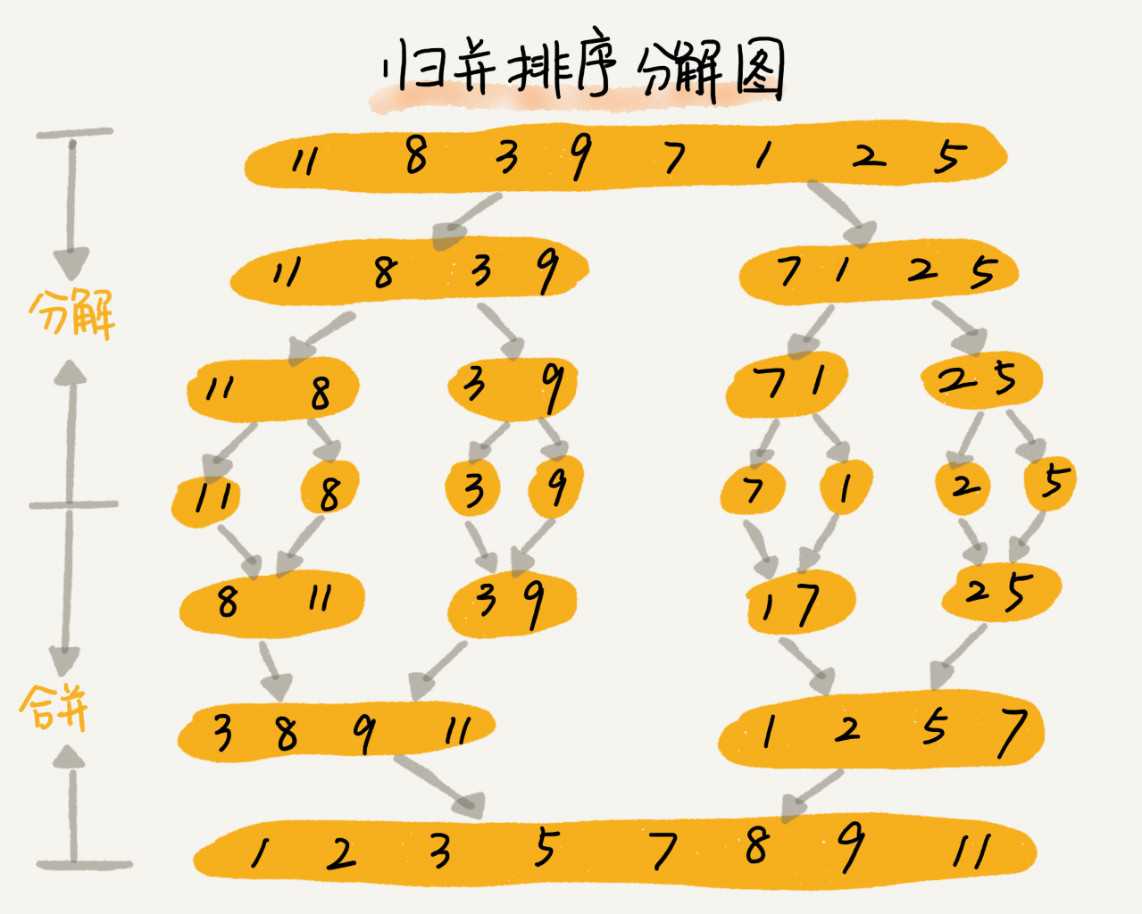
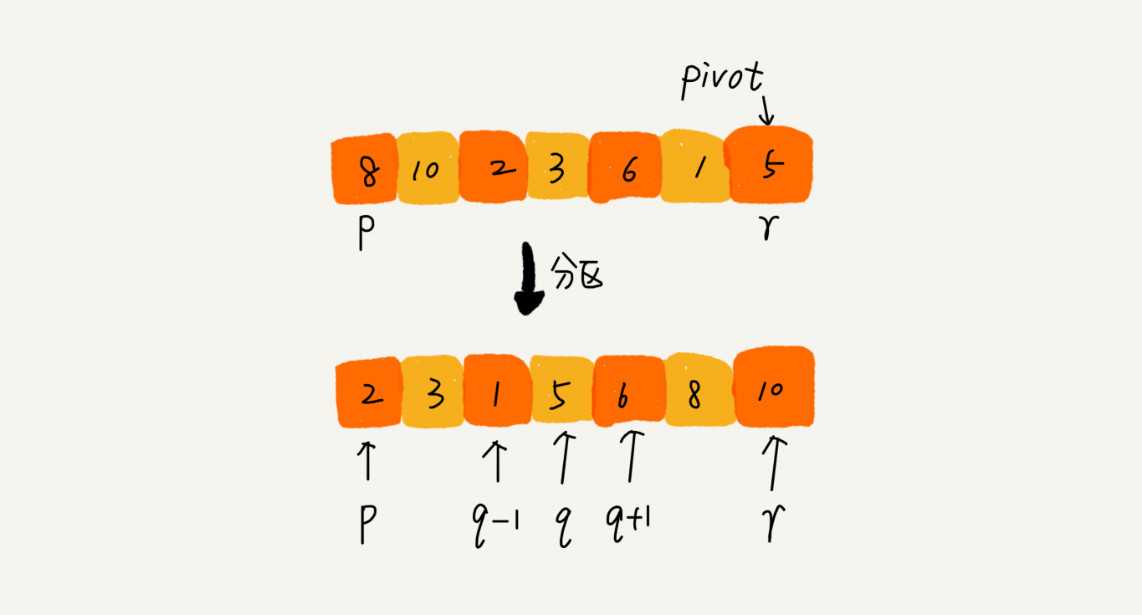
标签:temp 缩小 数组 区别 需要 inf jpg void 复杂 ???????归并排序的核心思想还是蛮简单的。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。 ???????具体实现: ???????归并排序是一个稳定的排序算法。归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。归并排序不是原地排序算法。空间复杂度是 O(n)。 ???????快排的思想是这样的:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。 ???????我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。 ???????具体代码: ???????快排是一种原地、不稳定的排序算法。空间复杂度是 O(1)。快排的时间复杂度是 O(nlogn),极端情况下是 O(n)。 ???????归并排序的处理过程是由下到上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上到下的,先分区,然后再处理子问题。 ???????O(n) 时间复杂度内求无序数组中的第 K 大元素。比如,4, 2, 5, 12, 3 这样一组数据,第 3 大元素就是 4。 ???????我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot,对数组 A[0…n-1]原地分区,这样数组就分成了三部分,A[0…p-1]、A[p]、A[p+1…n-1]。 ???????如果 p+1=K,那 A[p]就是要求解的元素;如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间,我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。同理,如果 K
???????我们再来看,为什么上述解决思路的时间复杂度是 O(n)? ???????第一次分区查找,我们需要对大小为 n 的数组执行分区操作,需要遍历 n 个元素。第二次分区查找,我们只需要对大小为 n/2 的数组执行分区操作,需要遍历 n/2 个元素。依次类推,分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。 ???????如果我们把每次分区遍历的元素个数加起来,就是:n+n/2+n/4+n/8+…+1。这是一个等比数列求和,最后的和等于 2n-1。所以,上述解决思路的时间复杂度就为 O(n)。 排序(二) 标签:temp 缩小 数组 区别 需要 inf jpg void 复杂 原文地址:https://www.cnblogs.com/vmbn465/p/12938939.html归并排序
//author : OuChenlu
//date : 2020-5-22
//project : MergeSort
void merge_sort_init(int h[], int n) {
int *temp = new int[n];
merge_sort(h, 0, n - 1, temp);
}
void merge_sort(int h[], int left, int right, int temp[]) {
if (left 快速排序
//author : OuChenlu
//date : 2020-5-10
//project : QuickSort
void quick_sort(int h[], int left, int right) {
if (left >= right) return;
int pivot = h[right];
int i, j;
i = j = left;
for (; j 快排与归并的区别
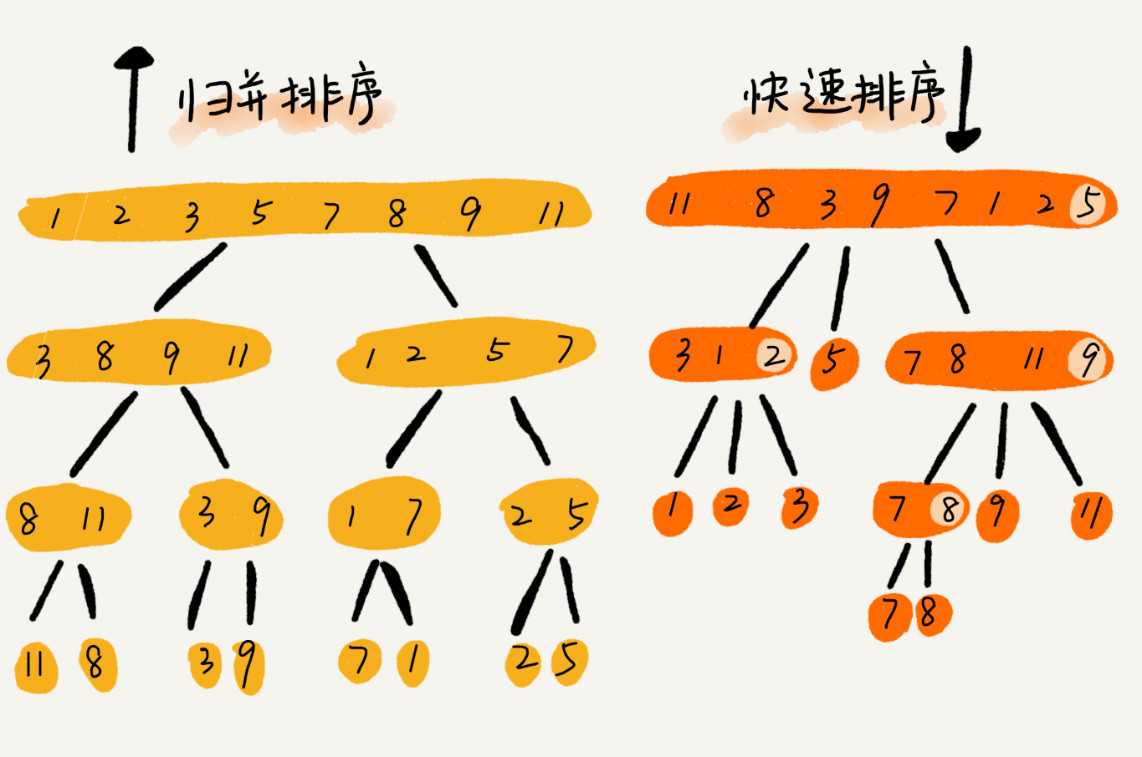
利用快排查找第 K 大元素