网络流最大流入门(Dinic算法)模板
2021-01-15 00:15
标签:set class 文章 using 元组 ace 重复 ddn 大致 本来先搞计算几何再搞网络流的,但是**总是发网络流的题,然后天天被信息组巨佬爆踩,所以先学一下最基本的Dinic算法吧。我也只是大致理解了流程,其实不懂也没事,只要会堆代码就好了(QAQ),所以下面只有教你如何堆代码啦(……)。 用cur[ ]代替变化的head[ ],dis[ ]表示到每个点到st的距离(每隔一条边距离就是1) 注意:题目不同,m和n的大小也不同,记得要更改呀~ 网络流最大流入门(Dinic算法)模板 标签:set class 文章 using 元组 ace 重复 ddn 大致 原文地址:https://www.cnblogs.com/mm-puppy-lyt/p/mm-puppy-wllzdlDinic.html前言
基本概念
图和收发点
容量和流量
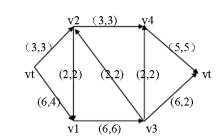
可行流


用途
当然就是求有向图中指定的某点到另一点的最大可行流(自己归纳的),解决这一问题的最好的算法就是Dinic了,下面给出具体流程。
算法流程
用n表示点数,m表示边数,st表示要求的起点,ed表示要求的终点(不专业术语,不要模仿呐)
首先存边
int head[],tot;
struct edge{int v,w,nxt;}e[];
void addn(int u,int v,int w){
e[++tot]=(edge){v,w,head[u]};
head[u]=tot;
}
//存边:u->v(w)和v->u(0)
addn(u,v,w);
addn(v,u,0);
然后码出每次dfs前需要的bfs建图
int bfs(int st,int ed)
{
//bfs建图
queueint>que;
memset(dis,-1,sizeof(dis));
dis[st]=0;
que.push(st);
while(!que.empty())
{
int x=que.front();
que.pop();
for(int i=head[x];i;i=e[i].nxt)
{
int now=e[i].v;
if(dis[now]==-1&&e[i].w)
{
que.push(now);
dis[now]=dis[x]+1;
}
}
}
return dis[ed]!=-1;
}
接着码dfs查询
int dfs(int x,int t,int maxflow)
{
if(x==t) return maxflow;
int ans=0;
for(int i=cur[x];i;i=e[i].nxt)
{
int now=e[i].v;
if(dis[now]!=dis[x]+1||!e[i].w||ans>=maxflow) continue;
cur[x]=i;
int f=dfs(now,t,min(e[i].w,maxflow-ans));
e[i].w-=f;
if(i&1) e[i+1].w+=f;
else e[i-1].w+=f;
ans+=f;
}
if(!ans) dis[x]=-1;
return ans;
}
然后大致流程就出来了,不断重复:bfs建图,dfs查询改值,直到不能再进行
现在放出全部代码
//dinic板子
#include
完结~~第一篇学术文章;撒花撒花??ヽ(°▽°)ノ?
上一篇:java中组合模式详解和使用方法
下一篇:数组reduce方法的高级技巧