# [acwing 240] 食物链 [并查集]
标签:构造 ++i print 描述 using namespace 合并 name win
[acwing 240] 食物链 [并查集]
传送门
题意
ABC三种动物,食物链构成一个环形,,给出M个关于彼此关系的描述,判断有多少个假话。
思路
本题是并查集的一种比较新颖的用法,并查集一般用来维护集合,但是在这里主要是使用路径压缩来维护点和根之间的距离。
动物之间有三种关系(同类,捕食,被捕食),并且食物链构成环,那么可以使用和根之间的距离模3来区分三种关系,这里并不严格划分集合,主要是借助了并查集中的路径压缩。
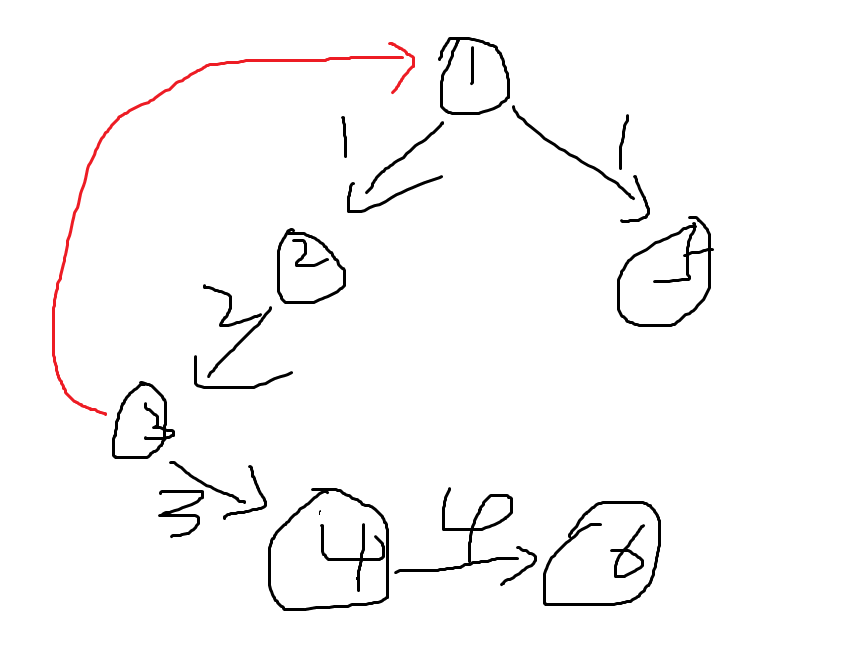
红色的线是不存在的,只是为了方便理解。图中的关系是:
- 2吃1 ,3吃2,4吃3,6吃4,5吃1。
- 其中3被1和4吃,那么1和4是同类(因为食物链是环形的,吃同一种动物的就是同类),1和4到1的距离模3都是0。
- 2,5,6是同类,模3都是1,都是1的捕食者
使用d[]维护节点x到父节点的距离,路径压缩时只要更新d[]的值
Code:
#include
using namespace std;
const int maxn=5e4+10;
int n,m;
int p[maxn],d[maxn];
inline int find(int x){
if(p[x]==x)return x;
int t=find(p[x]);
d[x]+=d[p[x]];//x节点到父节点p[x]的距离加上父节点到父父节点的距离,递归可得到根节点的距离
p[x]=t;//最终父节点更新成根节点
return p[x];
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;in||y>n)ans++;
else {
int px=find(x),py=find(y);
if(r==1){
if(px==py&&(d[x]-d[y])%3)ans++;//同一颗树上,同类的动物模3同余
else if(px!=py){//不在一个集合,无法判断是错误,那么是正确,那么构造同类关系
p[px]=py;
//合并的时候d[px]+d[x]和d[y]模3同余,即(d[px]+d[x]-d[y])%3==0
//可以认为d[px]=d[y]-d[x]。其他关系同理
d[px]=d[y]-d[x];
}
}
else {//x吃y
if(px==py&&(d[x]-d[y]-1)%3)ans++;
else if(px!=py){
p[px]=py;
d[px]=d[y]+1-d[x];
}
}
}
}
printf("%d\n",ans);
return 0;
}
# [acwing 240] 食物链 [并查集]
标签:构造 ++i print 描述 using namespace 合并 name win
原文地址:https://www.cnblogs.com/sstealer/p/12234102.html
评论
