特征工程:利用卡尔曼滤波器处理时间序列(快速入门+python实现)
2021-01-16 13:16
标签:http lan ado chm val mat guess pytho 偏差 假设我们有100个时间点的数据,这个数据就是分别在100个点观测出来的结果。 对于每一个时间点的数据,获取的方法有两个: 每一个观测数据,严谨的说都应该会有一个偏差值。比方说,现在温度计测量是26度,偏差值是0.5度,那么真实的问题应该是在(25.5,26.5)之间,或者写成\(26\pm0.5\)。 这样我们预测的值,和观测的值,再加上这两个各自的偏差,总共四个已知信息,来推测真实的、更本质的数据。 下面的公式中,脚标k表示时间点,k-1是上一个时间点。大写字母A,B,C表示常数,事先设定的;大写字母H,是一个需要计算的。 其中\(u_{k-1}\)表示上一个时间点的控制信号,比方说一个机器人,机器人的状态去觉得机器人自身的行为,但是很多情况这个控制信号是不用考虑的。比方对股市的时间序列做kalman滤波,那么并没有什么控制信号去控制,只是任由其自由发展。 举一个例子,房间的温度的例子: 最后总结一下,其实我们只需要什么呢?需要知道观测的误差是0.5,然后三个时间点的观测数据:[23,25,20],然后用kalman滤波器之后,就变成[23,24,6,22,56]。其实起到了一个平滑的作用。 这里面使用的是pykalman库中的KalmanFilter,因为上面讲解的Kalman Filter是简化的,绕靠了正统的解释的正态分布的知识,所以这里的卡尔曼滤波器的参数可能无法与上面给出的卡尔曼公式中一一对应,会产生一定的脱节。 这里讲一下参数: 从上面的那个函数中,可以看到transition_covariance是0.1,也就是预测偏差时0.1,所以假设观测偏差很小,那么可以想象,滤波器后的结果应该与观测值非常接近,这里选取观测偏差为0.001: 特征工程:利用卡尔曼滤波器处理时间序列(快速入门+python实现) 标签:http lan ado chm val mat guess pytho 偏差 原文地址:https://www.cnblogs.com/PythonLearner/p/12925724.html卡尔曼滤波器
为什么要用kalman filter处理时间序列
简单讲讲kalman filter的过程
可以看出,这个kalman增益就是一个加权平均的权重,是观测值更重要还是预测值更重要;两者的重要性就由两者的偏差大小决定,偏差小的更重要。
总共有三个时刻,上午、下午和晚上(实际的话,时间点间隔应该会很短,这里只是举例),上午温度是观测值是23度,偏差是0.5,因为上午是第一个时间点,所以没有预测值;
下午,假设A=1,B=0,所以下午的预测值是23度,然后假设初始偏差时1;下午的观测值是25度,观测值的偏差时0.5,所以可以计算得到kalman增益\(H=\frac{1^2}{1^2+0.5^2}=0.8\),所以下午的真实值是:\(0.8*25+(1-0.8)*23=24.6\)
晚上,晚上的预测值就是上一时刻的真实值,所以是24.6,偏差是\(\sqrt{(1-0.8)*1}=0.4472\);晚上的观测值是20度,然后偏差时0.5,所以kalman增益增益\(H=\frac{0.4472^2}{0.4472^2+0.5^2}=0.4444\),所以这个时刻的真实值是:\(0.4444*20+(1-0.4444)*24.6=22.56\)python怎么实现呢?
from pykalman import KalmanFilter
def Kalman1D(observations,damping=1):
# To return the smoothed time series data
observation_covariance = damping
initial_value_guess = observations[0]
transition_matrix = 1
transition_covariance = 0.1
initial_value_guess
kf = KalmanFilter(
initial_state_mean=initial_value_guess,
initial_state_covariance=observation_covariance,
observation_covariance=observation_covariance,
transition_covariance=transition_covariance,
transition_matrices=transition_matrix
)
pred_state, state_cov = kf.smooth(observations)
return pred_state
运行结果
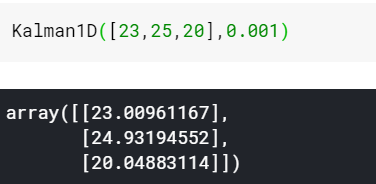
然后假设观测误差很大,那么可以想想,平滑的力度会很大,结果就是: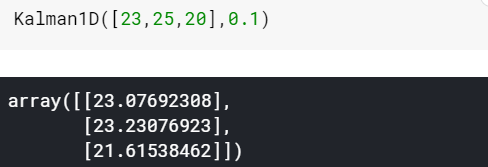
最后看一下在某次比赛中的利用kalman滤波器来平滑数据的前后对比图: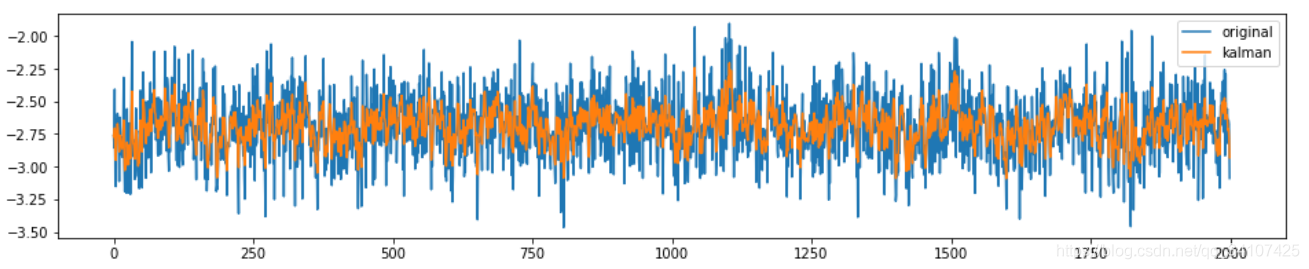
文章标题:特征工程:利用卡尔曼滤波器处理时间序列(快速入门+python实现)
文章链接:http://soscw.com/essay/42733.html