详解堆排序算法
2021-01-17 16:12
标签:为什么 heap port ++ 交换 tps 执行 eva 存储 堆首先是一个完全二叉树,堆分为大顶堆和小顶堆; 如图: 首先其为一个完全二叉树,且其每个节点的值都大于或者等于其左右孩子节点的值。 由大顶堆定义知道,如果我们从上到下,从左到右,根节点开始从0编号进行顺序存储的话,并将数组记为arr; 本文以大顶堆为例,进行讲解。 给定一个待排序序列数组 arr = [ 0 , 2, 4, 1 , 5 ]; 我们从最后一个非叶子节点开始,从左至右,从下到上,开始调整; 我们用左右孩子节点的最大值与该节点进行比较; 然后处理下一个非叶子节点,即刚才的索引减去1; 1 - 1 = 0; 左右孩子节点为5和4,5最大,且大于该节点的值,发生交换; 这时我们发现了一个问题: 继续进行调整: 对非叶子节点调整完毕,构建大顶堆完成。 将堆顶元素与末尾元素进行交换,使得末尾元素最大。 当交换完毕后最大的元素已经到达数组末尾; 对数组中其他元素进行排序即可。 进行交换: 剩下的元素调整并交换后: 剩下的元素调整并交换后: 此时也意味着排序完成了。 先说下调整的代码; 再说下堆排序代码,看好注释; 完整代码 在建初始堆时,其复杂度为$O(n)$; 堆排序是不稳定的: 当堆顶元素10和末尾元素交换后,两个9的相对位置发生改变。 欢迎大家的关注 扫描下方的二维码或者微信搜一搜即可关注我的微信公众号:code随笔 详解堆排序算法 标签:为什么 heap port ++ 交换 tps 执行 eva 存储 原文地址:https://www.cnblogs.com/nicaicai/p/12918205.html什么是堆
大顶堆 :
每个节点的值大于或等于其左右孩子节点的值,称为大顶堆。
小顶堆同理就是每个节点的值小于或等于其左右孩子节点的值。
注意:
每个节点的左右孩子节点的大小关系并没有限定。大顶堆举例
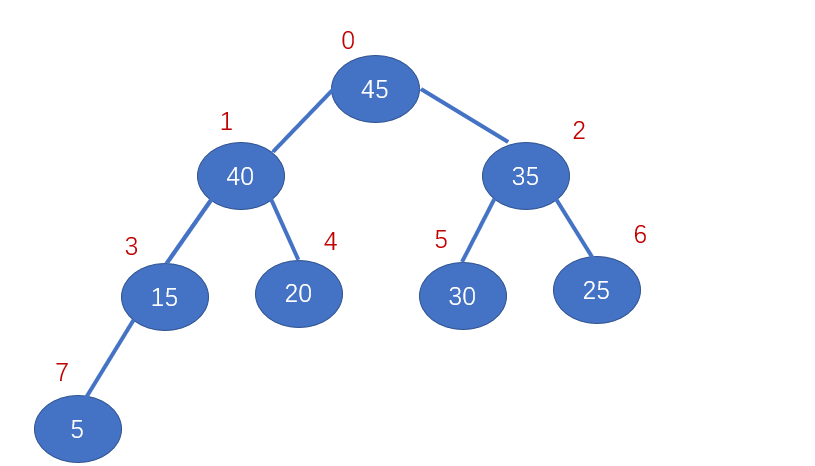
完全二叉树从上到下,从左到右依次编号,就可以将其进行顺序存储,我们从根节点开始,从0开始编号,存入数组如下: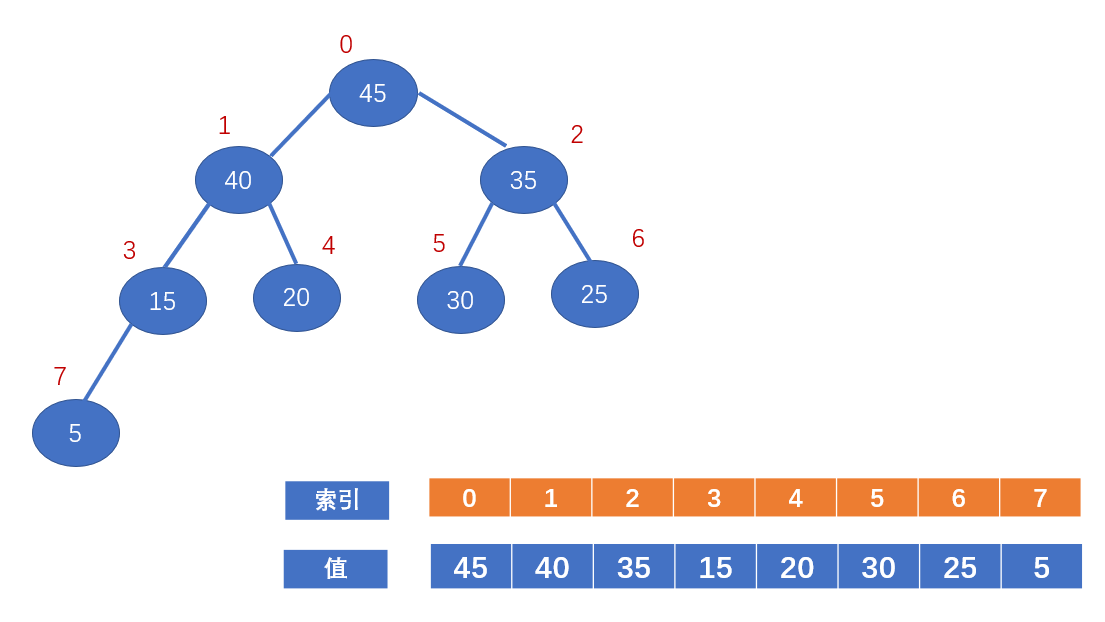
堆特点
我们可以得到如下式子:
arr[i] >= arr[ 2i + 1] && arr[ i ] >= arr[ 2i + 2];
其中 2i + 1为第 i 个节点的左孩子节点的编号。2i + 2为第 i 个节点的右孩子节点的编号;
同理得小顶堆的特点:
arr[i]
堆排序基本思想
算法步骤如下:
1、首先将待排序序列构建成一个大顶堆(存入数组中),那么这时,整个序列的最大值就是堆顶的根节点;
2、将堆顶元素与最后一个元素交换,那么末尾元素就存入了最大值;
3、将剩余的 n - 1个元素重新构建成一个大顶堆,重复上面的操作;
反复执行,就能得到一个有序序列了。举例
先构建成一个完全二叉树如下;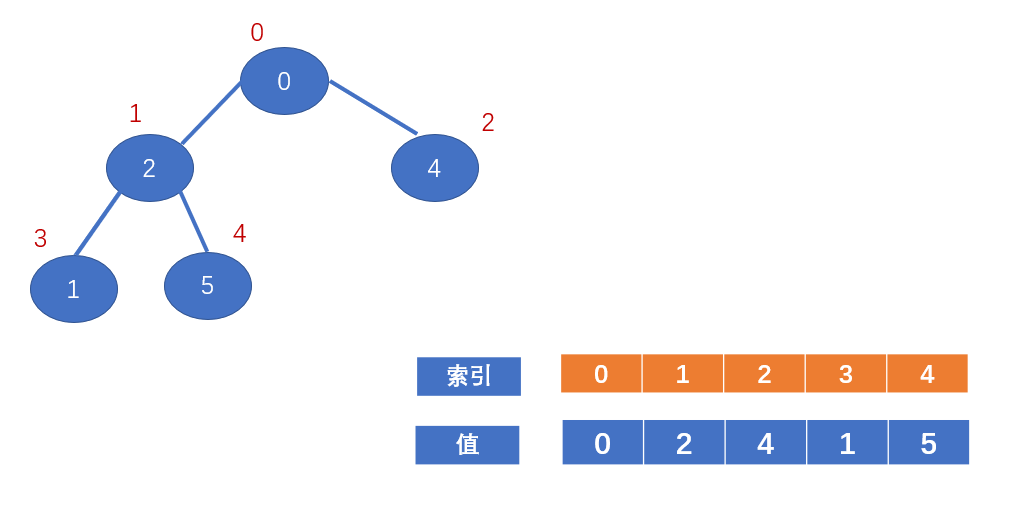
构建堆
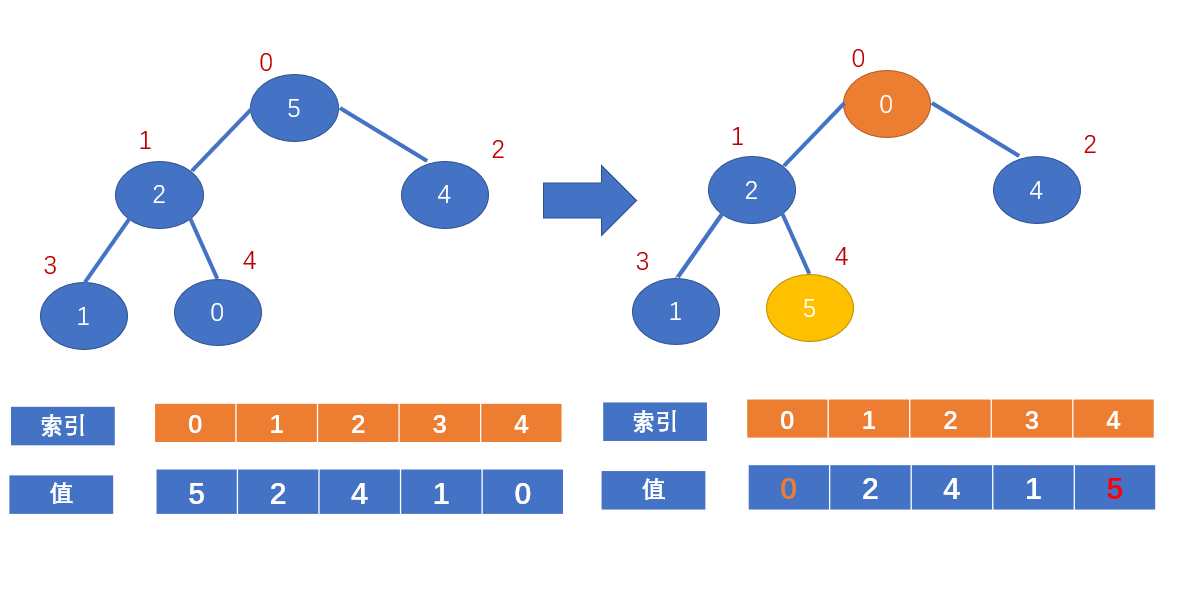
最后一个非叶子节点的索引即 arr.length / 2向下取整 - 1 ,对于此例就是 5 / 2向下取整 - 1 = 2 - 1 = 1;
即值为2的节点;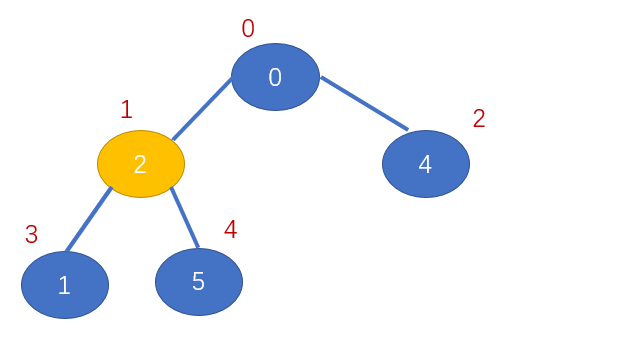
此时我们发现它的左右孩子节点的最大值为5,大于2,进行交换;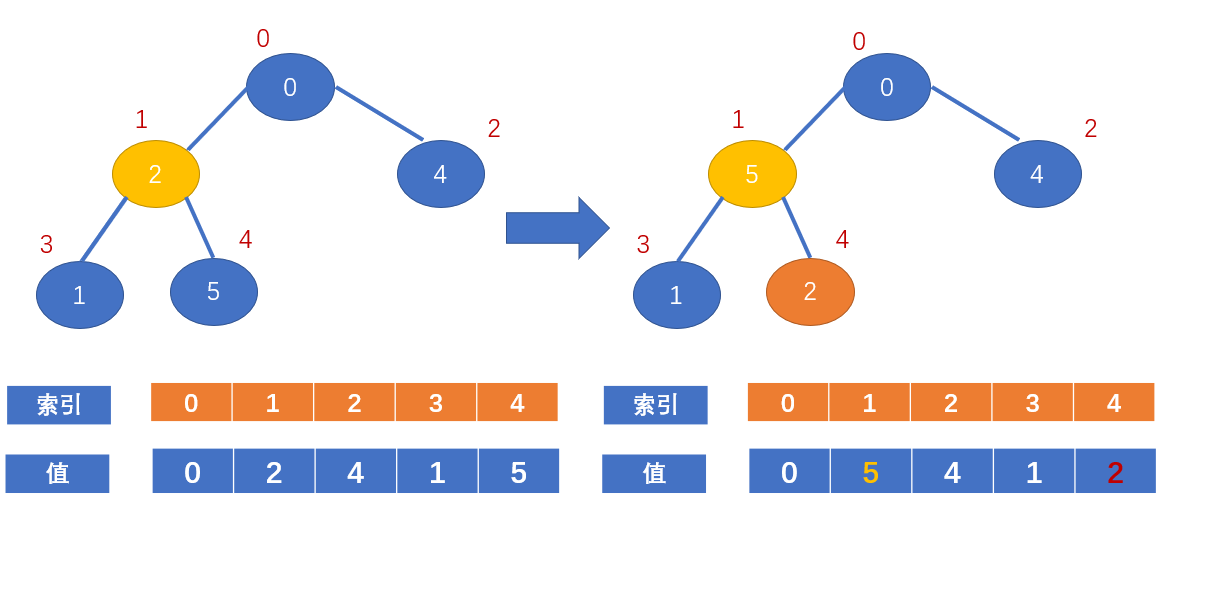
即: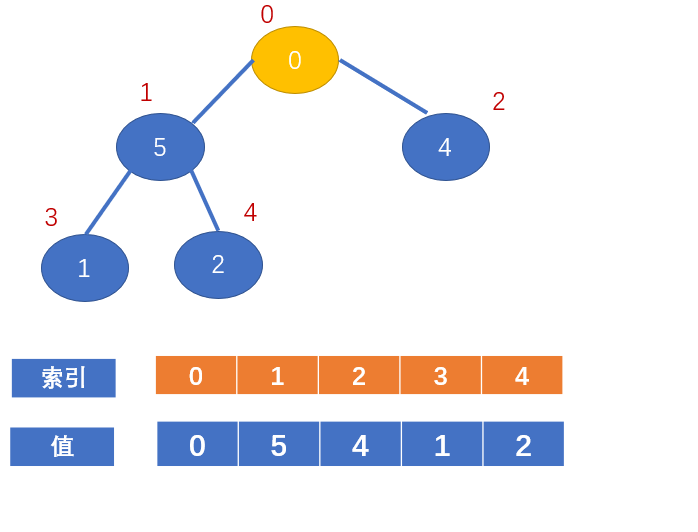
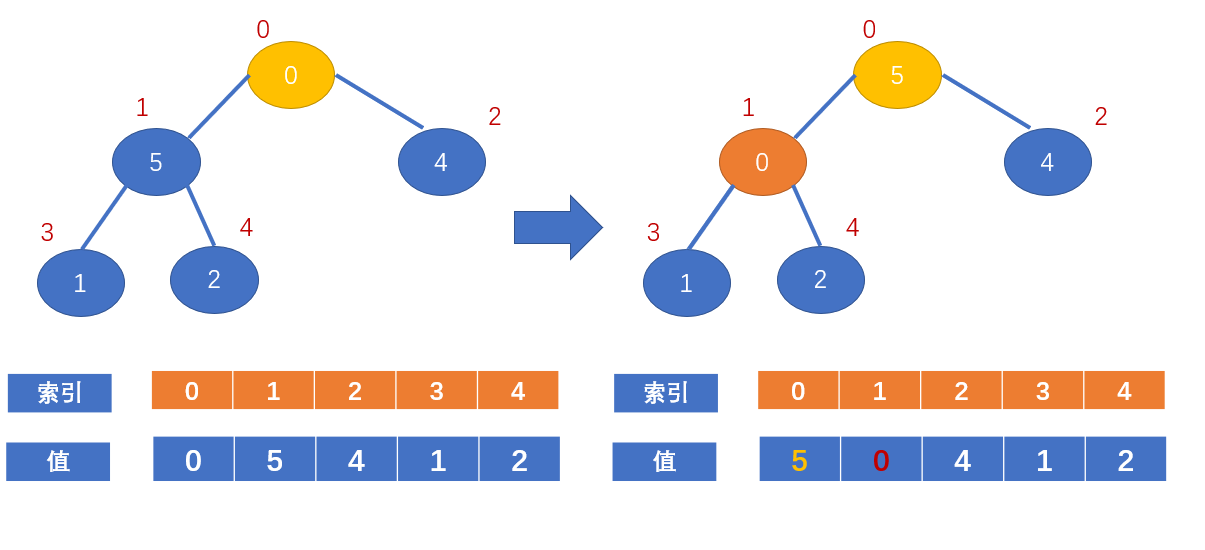
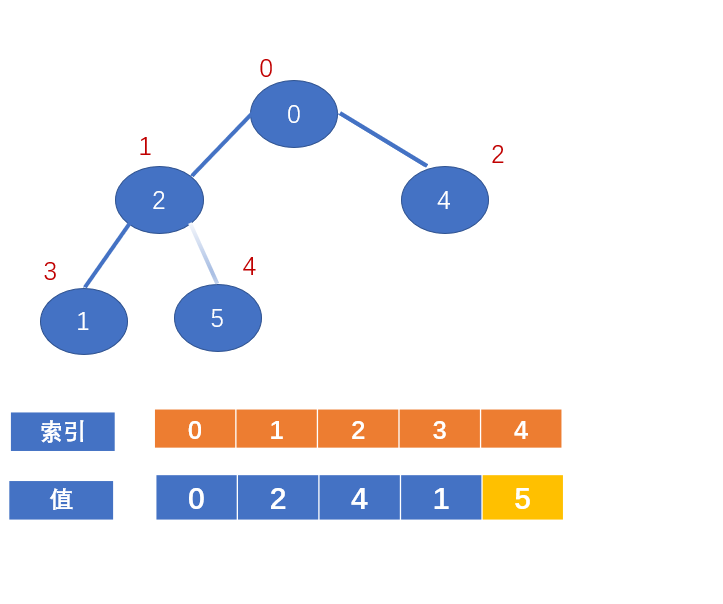
值为0的节点的左右节点又比该节点大了,又不满足大顶堆的定义了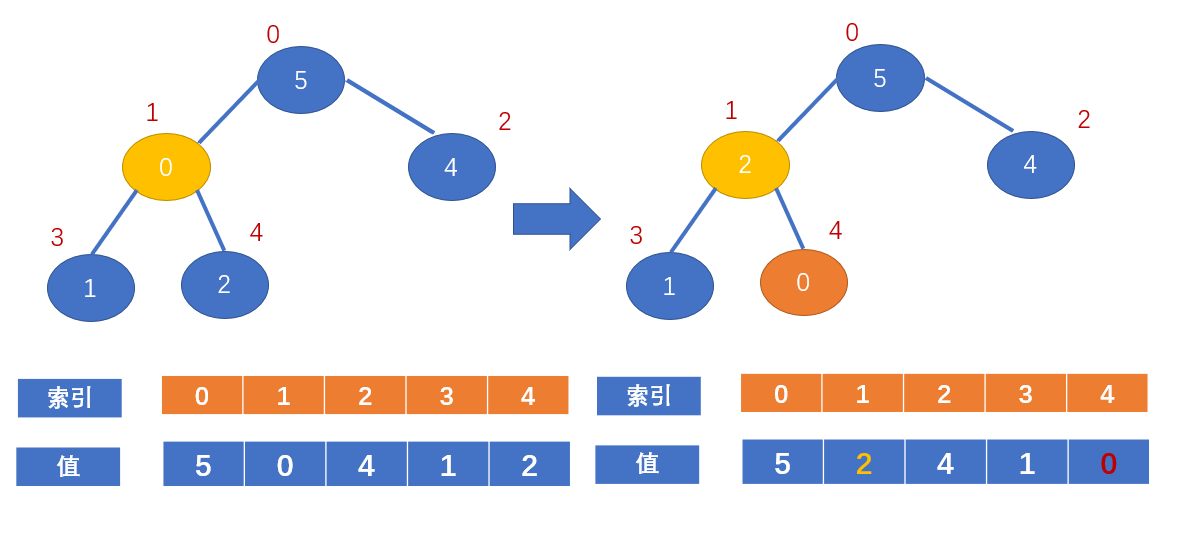
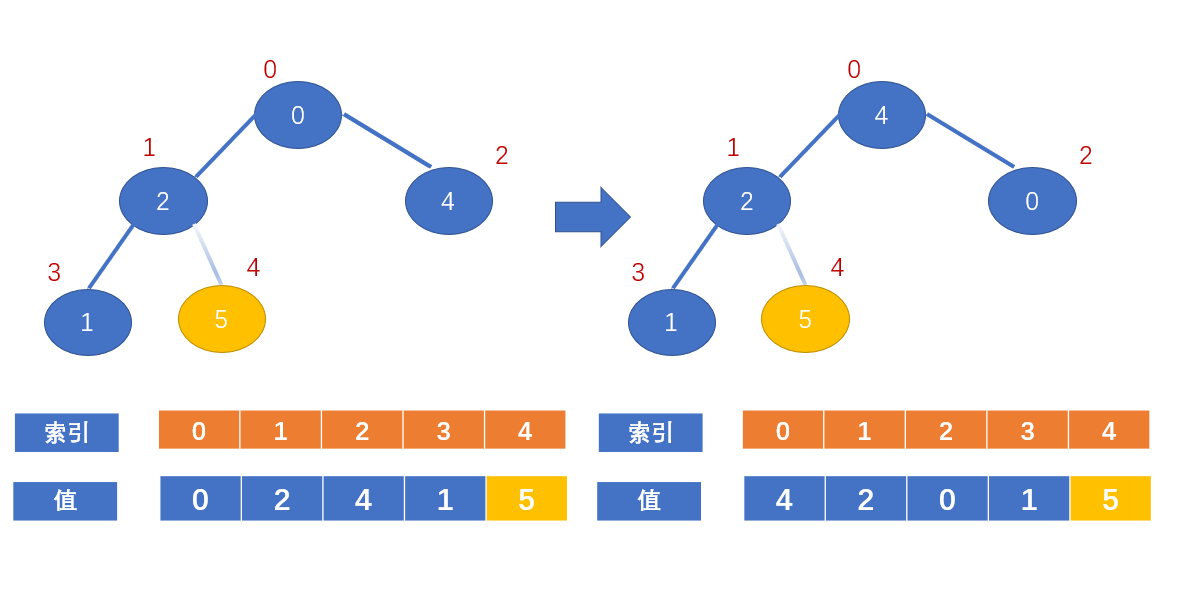
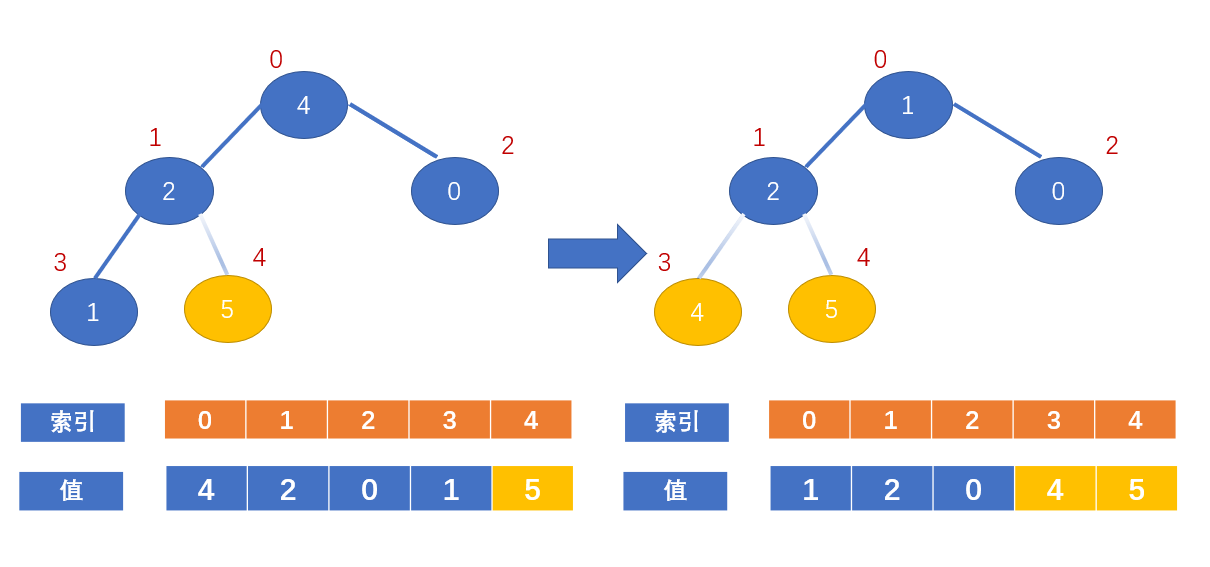
交换
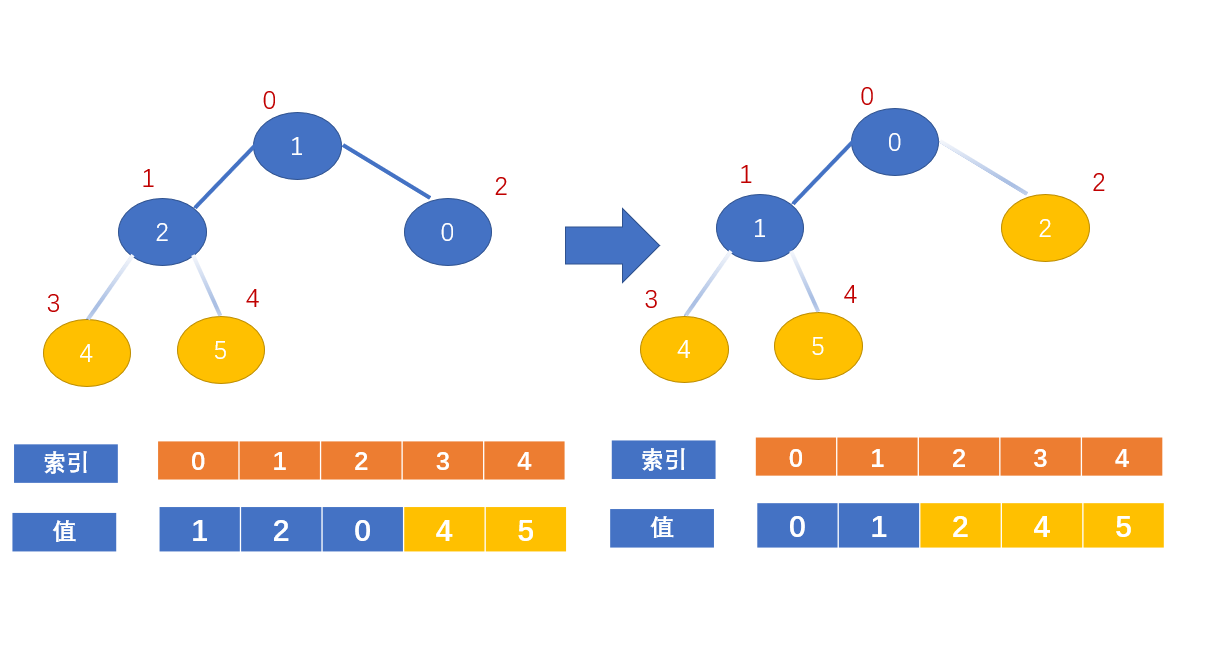

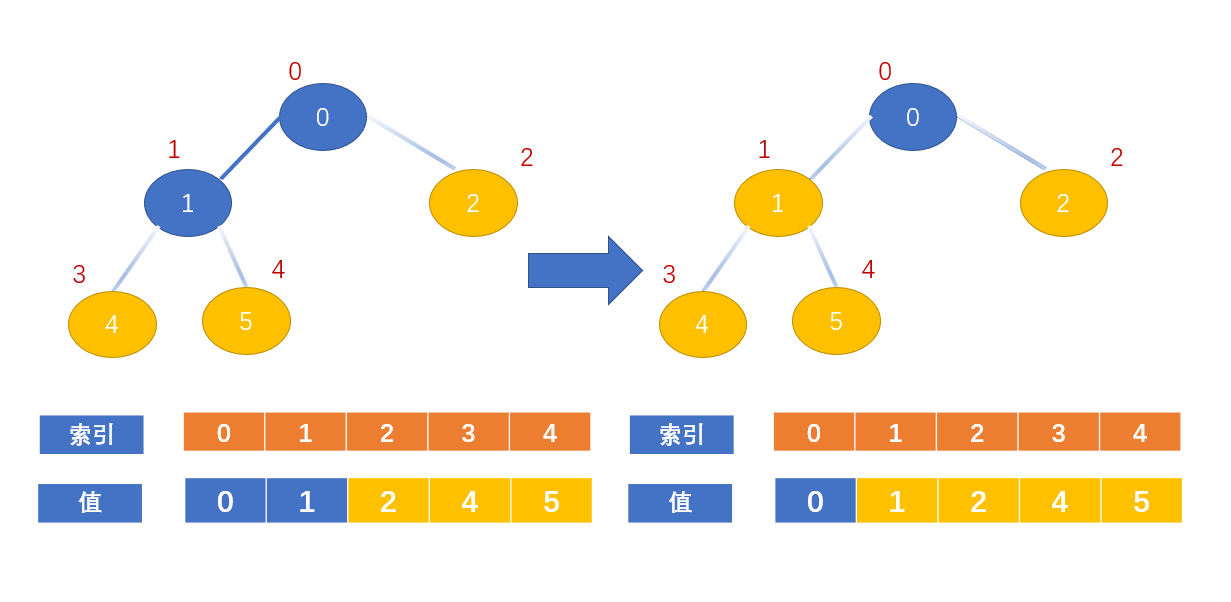
代码
我们需要三个参数,待排序的数组,数组的长度,还有一个就是调整的哪一个非叶子节点; /**
* author:微信公众号:code随笔
* @param arr 待排序的数组
* @param i 表示等待调整的哪个非叶子节点的索引
* @param length 待调整长度
*/
public static void adjustHeap(int arr[],int i,int length){
//非叶子节点的值
int notLeafNodeVal = arr[i];
//k的初始值为当前非叶子节点的左孩子节点的索引
//k = 2 * k + 1表示再往左子节点找
for(int k = i * 2 + 1;k//堆排序方法
public static void heapSort(int arr[]){
//进行第一次调整
for(int i=arr.length/2 - 1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
for(int j=arr.length - 1;j>0;j--){
//进行交换
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
//调整长度为j的那些
//这里为什么填0呢
//因为我们第一次调整的时候从左到右,从下到上调整的;
//交换时只是变动了堆顶元素和末尾元素
//末尾元素我们不用去管,因为已经是之前长度最大的了
//只需要把当前堆顶元素找到合适的位置即可
adjustHeap(arr,0,j);
}
}
import java.util.Arrays;
public class Solution {
public static void main(String[] args) {
int [] arr = new int[]{0 , 2, 4, 1 , 5};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
//堆排序方法
public static void heapSort(int arr[]){
//进行第一次调整
for(int i=arr.length/2 - 1;i>=0;i--){
adjustHeap(arr,i,arr.length);
}
for(int j=arr.length - 1;j>0;j--){
//进行交换
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
//调整长度为j的那些
//这里为什么填0呢
//因为我们第一次调整的时候从左到右,从下到上调整的;
//交换时只是变动了堆顶元素和末尾元素
//末尾元素我们不用去管,因为已经是之前长度最大的了
//只需要把当前堆顶元素找到合适的位置即可
adjustHeap(arr,0,j);
}
}
/**
* author:微信公众号:code随笔
* @param arr 待排序的数组
* @param i 表示等待调整的哪个非叶子节点的索引
* @param length 待调整长度
*/
public static void adjustHeap(int arr[],int i,int length){
//非叶子节点的值
int notLeafNodeVal = arr[i];
//k的初始值为当前非叶子节点的左孩子节点的索引
//k = 2 * k + 1表示再往左子节点找
for(int k = i * 2 + 1;k时间复杂度
交换操作需 n-1 次;
重建堆的过程中近似为$nlogn$;
堆排序时间复杂度为$O(nlogn)$。稳定性
比如:10,9,6,9;
如图: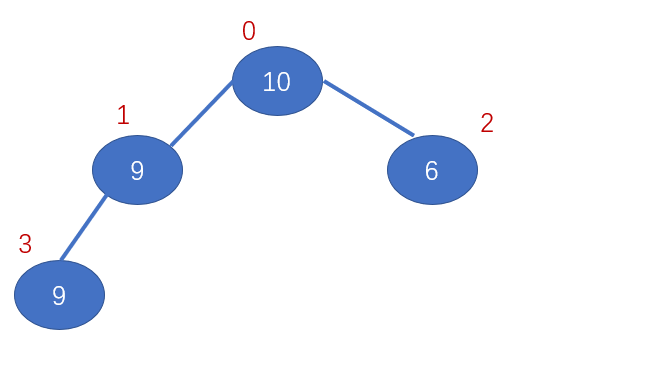
欢迎关注

上一篇:复习一下 Python三元运算