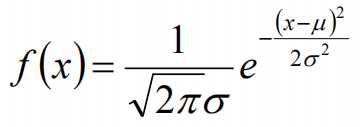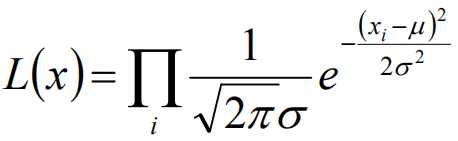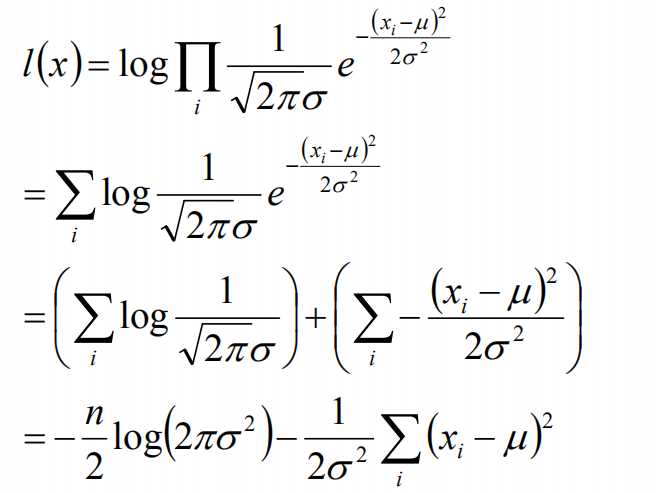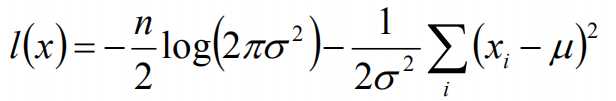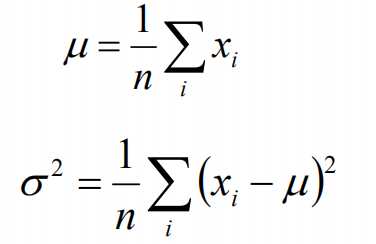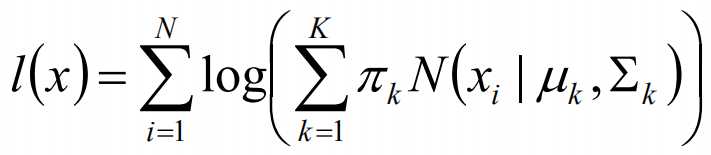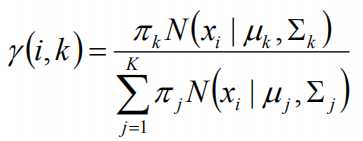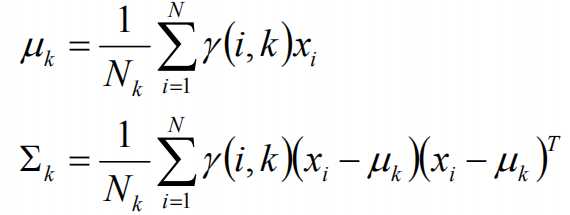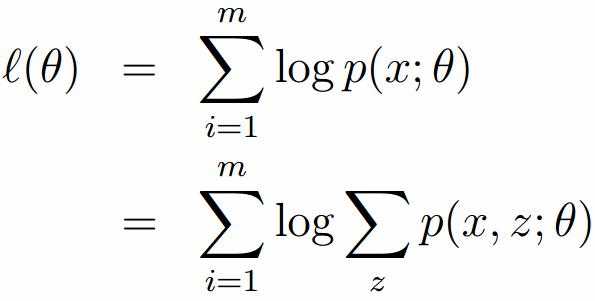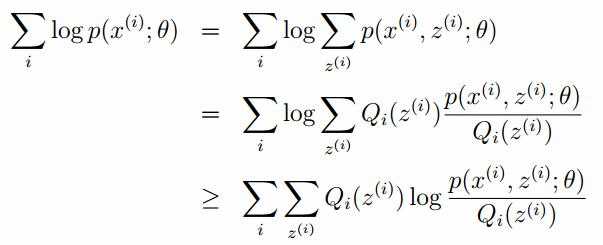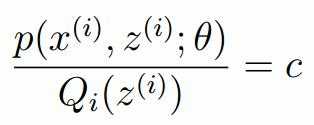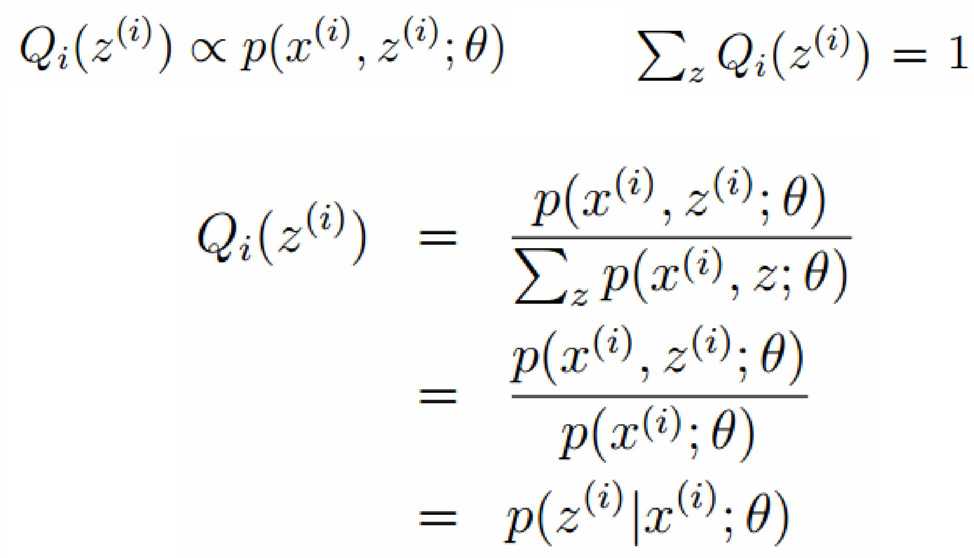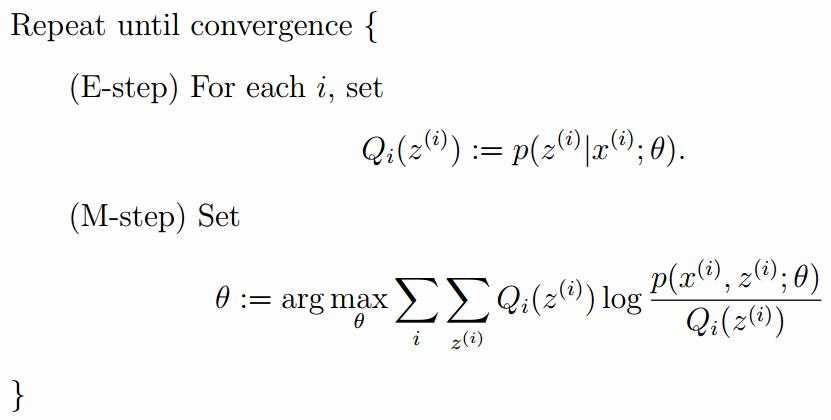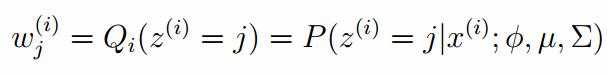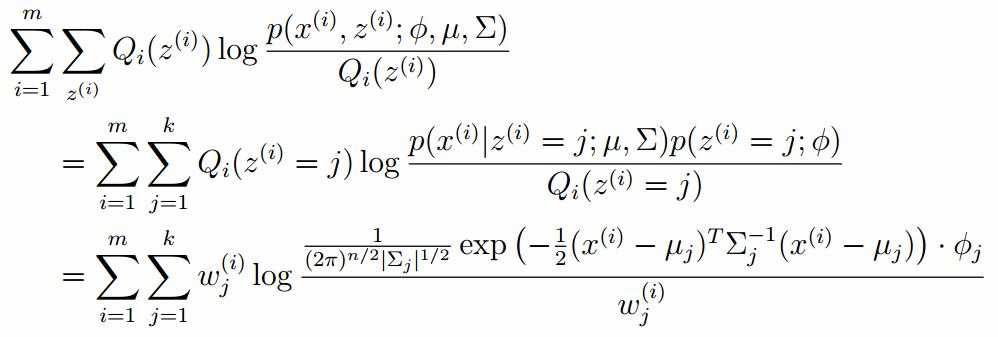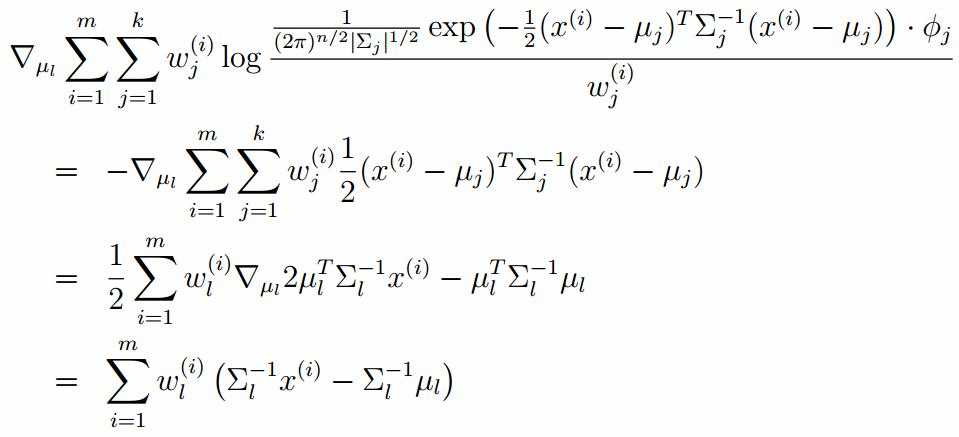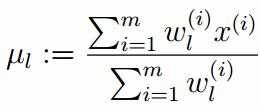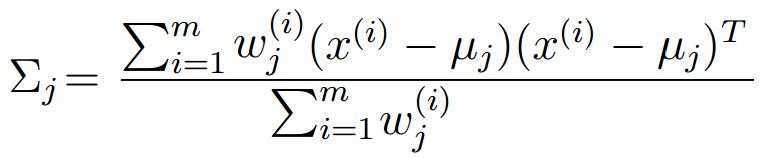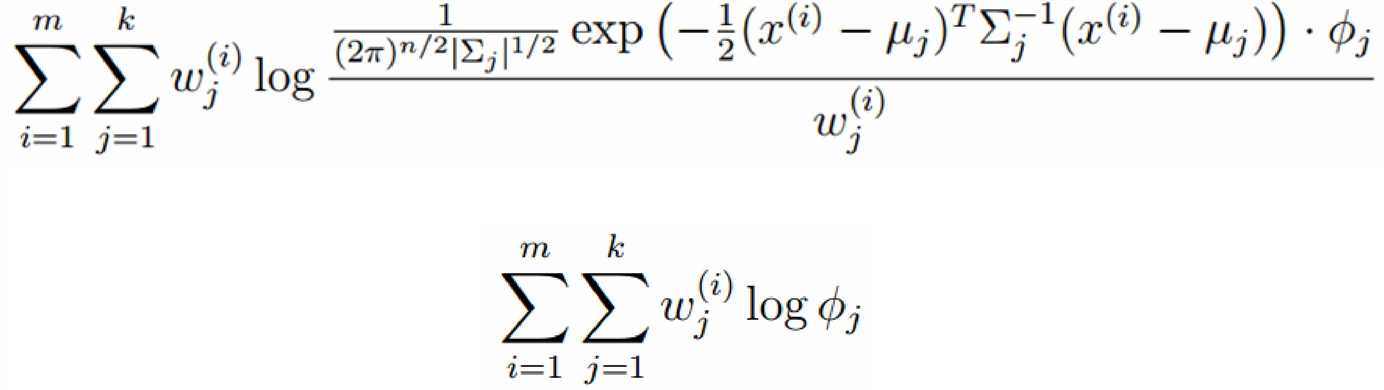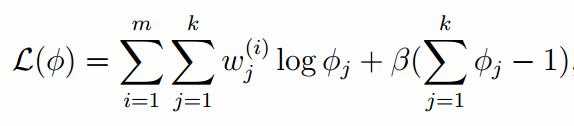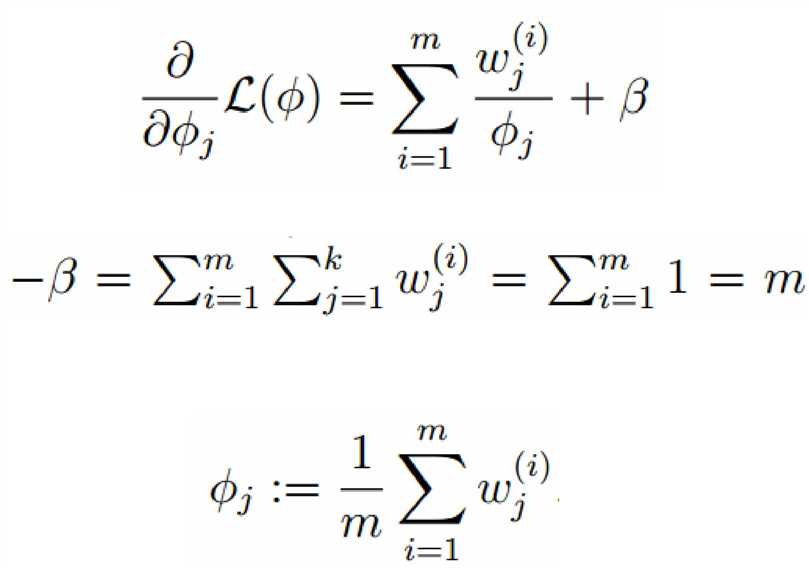EM算法和GMM算法的相关推导及原理
2021-01-18 10:15
标签:width 观测 理论 概率 现在 问题分析 参数 目标 span 极大似然估计 我们先从极大似然估计说起,来考虑这样的一个问题,在给定的一组样本x1,x2······xn中,已知它们来自于高斯分布N(u, σ),那么我们来试试估计参数u,σ。 首先,对于参数估计的方法主要有矩估计和极大似然估计,我们采用极大似然估计,高斯分布的概率密度函数如下: 我们可以将x1,x2,······,xn带入上述式子,得: 接下来,我们对L(x)两边去对数,得到: 于是,我们得到了l(x)的表达式,下面需要对其计算极大值: 通过对目标函数的参数u,σ分别求偏导,很容易得到: 对于上述的结果,和矩估计是一样,它的含义就是:样本的均值即为高斯分布的均值,样本的方差即为高斯分布的方差。 通过上面的问题分析,我们来看这样的一个问题,假设在班级中随机挑选100名同学,并且测量了这100名同学的身高,如果这100个样本服从的是正态分布,那么我们可以用样本的均值和方差等于正态分布的均值和方差来估计参数u和σ。但是样本中存在男同学和女同学,它们分别服从N1(u1, σ1)和N2(u2, σ2)的分布,那么我们应该如何估计u1, σ1,u2, σ2参数呢? 我们可以通过假设随机变量x是有k个高斯分布混合而成,取各个高斯分布的概率的φ1,φ2,······φk,第i个高斯分布的均值为ui,方差为∑i。那么,我们可以建立如下目标函数: 上述的式子中,由于在对数函数中存在加和,无法直接求导计算极大值,我们可以将其分成两步: 第一步:估算数据来自哪个组份 估计数据是有哪个组份生成的概率,对于数据xi来说,它是由第k个组份生成的概率为: 在上面的式子中,u和∑是需要进行估计的,这里采用迭代法,在计算r(i,k)的时候,假定u和∑均为已知的,但是在第一次计算时,我们根据先验知识给定u和∑。 第二步:估计每个组份的参数 假设上一步中得到的r(i,k)就是正确的数据xi由组份k生成的概率,亦可以当做该组份在生成这个数据上所做的贡献,或者也可以看做xi其中r(i,k)*xi部分是由组份k所生成的。对于所有的数据点,现在司机上可以看作组份k生成了{γ(i,k)*xi|i=1,2,…N}这些点。组份k是一个标准的高斯分布,利用上面的结论: EM算法的提出 假定有训练集{x1, x2,····xm},包含m个独立样本,要求从中找到该组数据的模型p(x, z)的参数。通过构建极大似然估计建立目标函数: 在上面的式子中,z是隐随机变量,直接找到参数的估计是很困难的。这里我们采用建立目标函数的下界,并且求该下界的最大值,不断的重复这个过程,直到收敛到局部的最大值。 Jensen不等式 令Qi是z的某一个分布,并且Qi>=0,有: 我们需要寻找尽量紧的下界,为了使得等式成立: EM算法的整体框架 E-step M-step 对上面的公式求偏导 由于多项分布的概率和为1,建立拉个朗日方程: 计算偏导: EM算法和GMM算法的相关推导及原理 标签:width 观测 理论 概率 现在 问题分析 参数 目标 span 原文地址:https://www.cnblogs.com/baby-lily/p/12913012.html