机器学习算法及代码实现–支持向量机
2021-01-18 20:18
阅读:920
机器学习算法及代码实现–支持向量机
1、支持向量机
SVM希望通过N-1维的分隔超平面线性分开N维的数据,距离分隔超平面最近的点被叫做支持向量,我们利用SMO(SVM实现方法之一)最大化支持向量到分隔面的距离,这样当新样本点进来时,其被分类正确的概率也就更大。我们计算样本点到分隔超平面的函数间隔,如果函数间隔为正,则分类正确,函数间隔为负,则分类错误,函数间隔的绝对值除以||w||就是几何间隔,几何间隔始终为正,可以理解为样本点到分隔超平面的几何距离。若数据不是线性可分的,那我们引入核函数的概念,从某个特征空间到另一个特征空间的映射是通过核函数来实现的,我们利用核函数将数据从低维空间映射到高维空间,低维空间的非线性问题在高维空间往往会成为线性问题,再利用N-1维分割超平面对数据分类。 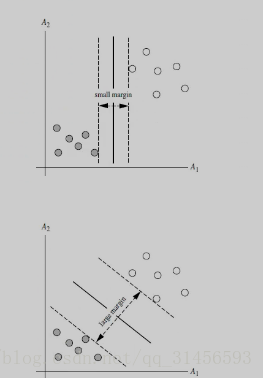
2、分类
线性可分、线性不可分
3、超平面公式(先考虑线性可分)
W*X+b=0
其中W={w1,w2,,,w3},为权重向量
下面用简单的二维向量讲解(思维导图) 
4、寻找超平面

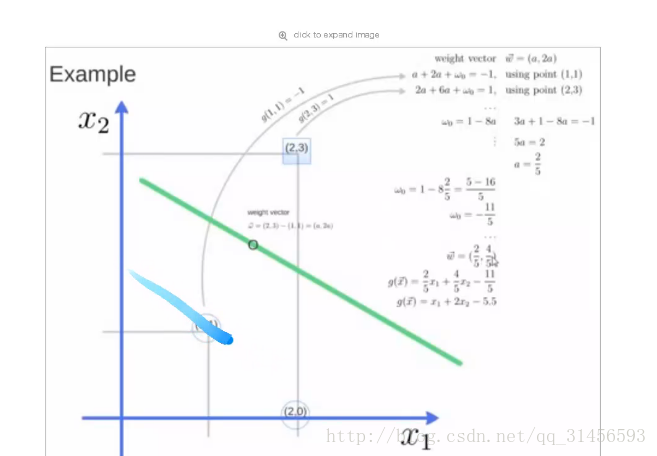
5、例子
6、线性不可分
映射到高维 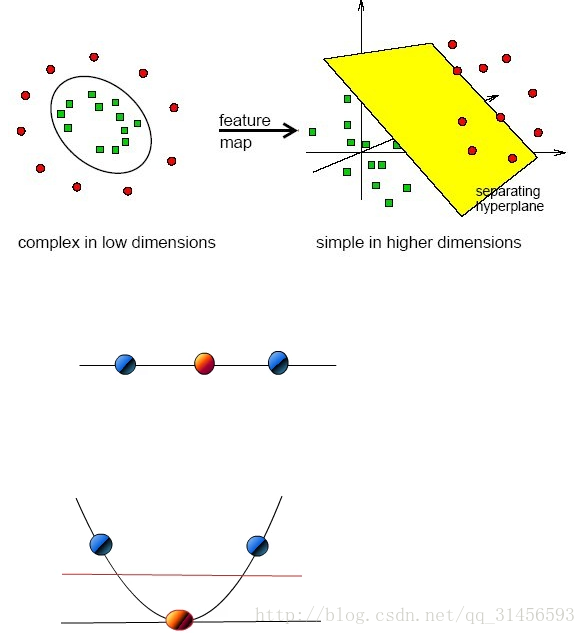
算法思路(思维导图)

核函数举例 
代码
# -*- coding: utf-8 -*- from sklearn import svm # 数据 x = [[2, 0], [1, 1], [2, 3]] # 标签 y = [0, 0, 1] # 线性可分的svm分类器,用线性的核函数 clf = svm.SVC(kernel=‘linear‘) # 训练 clf.fit(x, y) print clf # 获得支持向量 print clf.support_vectors_ # 获得支持向量点在原数据中的下标 print clf.support_ # 获得每个类支持向量的个数 print clf.n_support_ # 预测 print clf.predict([2, 0])
# -*- coding: utf-8 -*- import numpy as np import pylab as pl from sklearn import svm np.random.seed(0) # 值固定,每次随机结果不变 # 2组20个二维的随机数,20个0,20个1的y (20,2)20行2列 X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]] Y = [0] * 20 + [1] * 20 # 训练 clf = svm.SVC(kernel=‘linear‘) clf.fit(X, Y) w = clf.coef_[0] a = -w[0] / w[1] xx = np.linspace(-5, 5) yy = a * xx - (clf.intercept_[0] / w[1]) # 点斜式 平分的线 b = clf.support_vectors_[0] yy_down = a* xx +(b[1] - a*b[0]) b = clf.support_vectors_[-1] yy_up = a* xx +(b[1] - a*b[0]) # 两条虚线 print "w: ", w print "a: ", a # print " xx: ", xx # print " yy: ", yy print "support_vectors_: ", clf.support_vectors_ print "clf.coef_: ", clf.coef_ # In scikit-learn coef_ attribute holds the vectors of the separating hyperplanes for linear models. It has shape (n_classes, n_features) if n_classes > 1 (multi-class one-vs-all) and (1, n_features) for binary classification. # # In this toy binary classification example, n_features == 2, hence w = coef_[0] is the vector orthogonal to the hyperplane (the hyperplane is fully defined by it + the intercept). # # To plot this hyperplane in the 2D case (any hyperplane of a 2D plane is a 1D line), we want to find a f as in y = f(x) = a.x + b. In this case a is the slope of the line and can be computed by a = -w[0] / w[1]. # plot the line, the points, and the nearest vectors to the plane pl.plot(xx, yy, ‘k-‘) pl.plot(xx, yy_down, ‘k--‘) pl.plot(xx, yy_up, ‘k--‘) pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80, facecolors=‘none‘) pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired) pl.axis(‘tight‘) pl.show()
# -*- coding: utf-8 -*- from __future__ import print_function from time import time import logging # 打印程序进展的信息 import matplotlib.pyplot as plt from sklearn.cross_validation import train_test_split from sklearn.datasets import fetch_lfw_people from sklearn.grid_search import GridSearchCV from sklearn.metrics import classification_report from sklearn.metrics import confusion_matrix from sklearn.decomposition import RandomizedPCA from sklearn.svm import SVC print(__doc__) # 打印程序进展的信息 logging.basicConfig(level=logging.INFO, format=‘%(asctime)s %(message)s‘) ############################################################################### # 下载人脸数据集,并导入 lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4) # 数据集多少,长宽多少 n_samples, h, w = lfw_people.images.shape # x是特征向量的矩阵,获取矩阵列数,即纬度 X = lfw_people.data n_features = X.shape[1] # y是分类标签向量 y = lfw_people.target # 类别里面有谁的名字 target_names = lfw_people.target_names # 名字有多少行,即有多少人要区分 n_classes = target_names.shape[0] # 打印 print("Total dataset size:") print("n_samples: %d" % n_samples) print("n_features: %d" % n_features) print("n_classes: %d" % n_classes) ############################################################################### # 将数据集划分为训练集和测试集,测试集占0.25 X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.25) ############################################################################### # PCA降维 n_components = 150 # 组成元素数量 print("Extracting the top %d eigenfaces from %d faces" % (n_components, X_train.shape[0])) t0 = time() # 建立PCA模型 pca = RandomizedPCA(n_components=n_components, whiten=True).fit(X_train) print("done in %0.3fs" % (time() - t0)) # 提取特征脸 eigenfaces = pca.components_.reshape((n_components, h, w)) print("Projecting the input data on the eigenfaces orthonormal basis") t0 = time() # 将特征向量转化为低维矩阵 X_train_pca = pca.transform(X_train) X_test_pca = pca.transform(X_test) print("done in %0.3fs" % (time() - t0)) ############################################################################### # Train a SVM classification model print("Fitting the classifier to the training set") t0 = time() # C错误惩罚权重 gamma 建立核函数的不同比例 param_grid = {‘C‘: [1e3, 5e3, 1e4, 5e4, 1e5], ‘gamma‘: [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], } # 选择核函数,建SVC,尝试运行,获得最好参数 clf = GridSearchCV(SVC(kernel=‘rbf‘, class_weight=‘auto‘), param_grid) # 训练 clf = clf.fit(X_train_pca, y_train) print("done in %0.3fs" % (time() - t0)) print("Best estimator found by grid search:") print(clf.best_estimator_) # 输出最佳参数 ############################################################################### # Quantitative evaluation of the model quality on the test set print("Predicting people‘s names on the test set") t0 = time() # 预测 y_pred = clf.predict(X_test_pca) print("done in %0.3fs" % (time() - t0)) print(classification_report(y_test, y_pred, target_names=target_names)) # 与真实情况作对比求置信度 print(confusion_matrix(y_test, y_pred, labels=range(n_classes))) # 对角线的为预测正确的,a预测为a ############################################################################### # Qualitative evaluation of the predictions using matplotlib def plot_gallery(images, titles, h, w, n_row=3, n_col=4): """Helper function to plot a gallery of portraits""" plt.figure(figsize=(1.8 * n_col, 2.4 * n_row)) plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35) for i in range(n_row * n_col): plt.subplot(n_row, n_col, i + 1) plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray) plt.title(titles[i], size=12) plt.xticks(()) plt.yticks(()) # plot the result of the prediction on a portion of the test set def title(y_pred, y_test, target_names, i): pred_name = target_names[y_pred[i]].rsplit(‘ ‘, 1)[-1] true_name = target_names[y_test[i]].rsplit(‘ ‘, 1)[-1] return ‘predicted: %s\ntrue: %s‘ % (pred_name, true_name) prediction_titles = [title(y_pred, y_test, target_names, i) for i in range(y_pred.shape[0])] plot_gallery(X_test, prediction_titles, h, w) # 画出测试集和它的title # plot the gallery of the most significative eigenfaces eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])] plot_gallery(eigenfaces, eigenface_titles, h, w) # 打印特征脸 plt.show() # 显示
评论
亲,登录后才可以留言!