C++动态规划01背包
2021-01-20 02:12
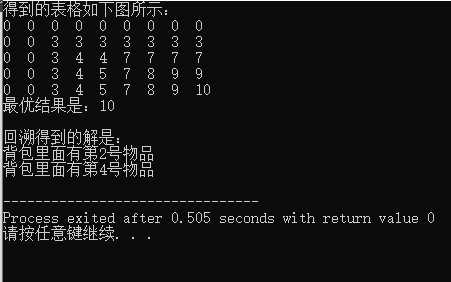
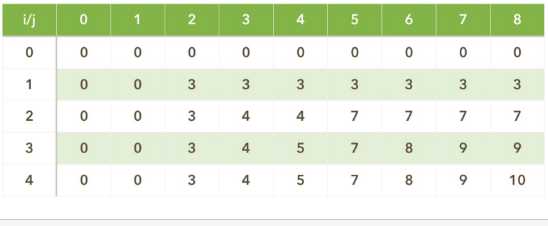
标签:结果 递推 amp 组合 nbsp oid for 变量 htm 动态规划01背包实现: 借鉴的这篇博文: https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html 题目:在背包容量为8的情况下,根据下图的数据动态规划得到最优解,实现右图所示的程序代码 最重要的就是寻找递推关系式: 定义V[i,j]:当背包容量为j时,前i个物品最佳组合对应的值。 递推关系: (1)当背包的容量不允许装入第i件物品时,和前一个物品装入背包一样。即 :V[i][j]=V[i-1][j] (2)当背包的容积可以装入第i件物品时,分两种情况,A装入第i件物品不是最优,还不如不装。B装入第i件物品是最优。即:V[i][j]=max(V[i-1][j],V[i][j-w[i]]+v[i]) 代码实现: 下面是带上回溯找出解的组成的代码: 贴上结果便于理解: 时间复杂度: O(物体个数*背包容积)=O(number*capacity) 空间复杂度: 用二维表实现的,所以和时间复杂度一样。 O(物体个数*背包容积)=O(number*capacity) C++动态规划01背包 标签:结果 递推 amp 组合 nbsp oid for 变量 htm 原文地址:https://www.cnblogs.com/zhaoxiansheng666/p/12905475.html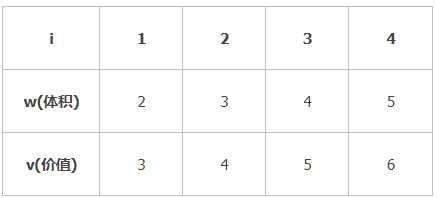
#include
#include