【Redis】跳跃表原理分析与基本代码实现(java)
2021-01-28 07:14
标签:else 规则 可见 rabl 浮点数 技术 超过 分析 需要 最近开始看Redis设计原理,碰到一个从未遇见的数据结构:跳跃表(skiplist)。于是花时间学习了跳表的原理,并用java对其实现。 主要参考以下两本书: 跳跃表是一种有序数据结构,它通过每个结点中维持多个指向其它结点的指针,从而达到快速访问结点的目的。 我们平时熟知的链表,查找效率为O(N)。跳表在链表的基础上,每个结点中维护了很多指向其它结点的指针,大大缩短时间复杂度。可以实现时间复杂度平均O(logN),最坏O(N)。后文会有具体的分析和计算。 一个跳跃表示意图: 最外层的跳表字段结构如下所示: 跳表节点记为SkipListNode,内部字段结构如下: 索引层SkipListLevel的结构如下: 到这里,我们对跳表的基本结构有了一个清晰的认识。 这里想先讲讲理想状态的跳表,不然无法理解实际跳表为什么可以缩减时间复杂度。 跳表节点间的关联方式:(索引层中的前向指针)第一层逐个链接,第二层每隔t个节点进行链接,第三层每隔2*t个节点进行链接,不断迭代。这里取t=2,画出每个节点的索引层之间的关联关系,得到如下图形式的链式结构: 有点像完全二叉树的结构。因此很容易理解:节点总数为N时,层最大高度为1+logN。例如图中有8个节点,最大层高为4。 搜索规则:从头结点的索引层的末端开始向下遍历。如果第K层的下一节点小于target,则移到该节点;若不小于,则下移到第K-1层。 按照此搜索规则,假设需要查找的target为7a,则搜索路径为0d--8d--0c--4c--4b--6b--6a--7a,如下图所示: 上述过程中,分别在8d、4c、6b、7a处进行比较。可见每一层都比较了一次,所以比较次数等于层数,为logN+1。所以时间复杂度为O(logN)。 如果实际的跳表按照这种形式进行设计,每次插入节点时,需要对很多结点的索引层进行调整,节点的插入删除将成为极其复杂的工作。因此,实际的跳表使用一种基于概率统计的算法,简化插入删除带来的调整工作,同时也能得到O(logN)的时间复杂度。 每当需要新增一个节点时,需要考虑如何确定该节点的索引层层数,即SkipListLevel[]数组的长度。 在redis中,每次创建一个节点,都会根据幂次定律随机生成一个介于1和32之间的值作为索引层的高度。问题是,这个随机的过程如何设计? 我们观察理想状态跳表,可以发现,不算头节点总共8个节点,其中4个节点拥有2层索引,2个节点拥有3层索引,1个节点拥有4层索引。 可以近似看作满足这样的规律:节点索引层高度为 j 的概率为 1/2^j。因此每次生成新节点时,通过这样的概率计算可以得到索引层层数。代码如下所示: 注意:在redis中最大索引高度不超过32 当节点数量足够多时,这种方式得到的跳跃表形态可以逼近理想的跳表的。很惭愧我不知道怎么证明,学过概率统计的同学一定很容易理解。它的时间复杂度就是近似为 O(logN) 。当然也有不理想的情况,当跳表中每一个节点随机得到的层高度都是 1 时,跳表就是一个普通双向链表,时间复杂度为 O(N) 。因此,时间复杂度平均O(logN)、最坏O(N),这种说法是比较严谨的。 这个分值 score 很容易与节点的“跨度”混淆。跨度其实就是节点在跳表中的排位,或者说序号。而分值是一个节点属性。节点按照分值大小由小到大排列,不同节点的分值可以相等。如果分值相等,对象较大的会排在后面(靠近表尾方向)。 在实际API应用中,需要以分值和obj成员对象作为target进行查询、插入等操作。 流程如下: 实际代码比上述流程要复杂很多,levelHeight与maxLevelHeight的大小关系不能确定,根据不同的情况要对update[]进行不同的处理。 跳跃表插入的代码如下所示: 注意:是依据score大小和obj的大小来决定插入顺序 本篇博客介绍了跳跃表基本原理,并使用java完成了基本数据结构的封装,实现了节点插入操作。后续博客会陆续记录“删除”、“搜索”等功能的实现。 【Redis】跳跃表原理分析与基本代码实现(java) 标签:else 规则 可见 rabl 浮点数 技术 超过 分析 需要 原文地址:https://www.cnblogs.com/buptleida/p/12838880.html
介绍
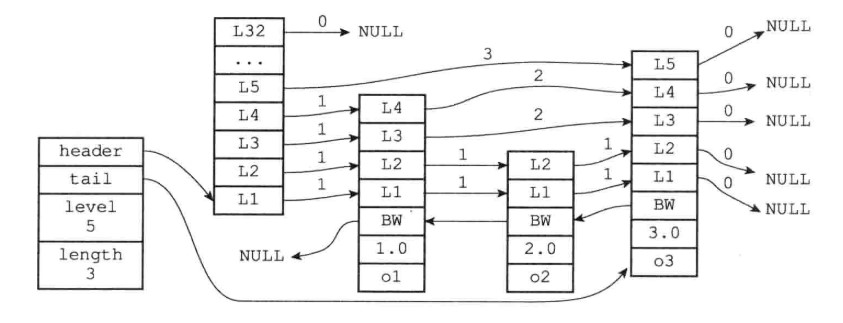
由左至右依次是,跳跃表结构结点(存储跳表信息)、头结点、连续的跳表结点。public class SkipList跳表节点
class SkipListNode
索引层
class SkipListLevel{
//前进指针
private SkipListNode forward;
//跨度
private int span;
//......
}
理想的跳表
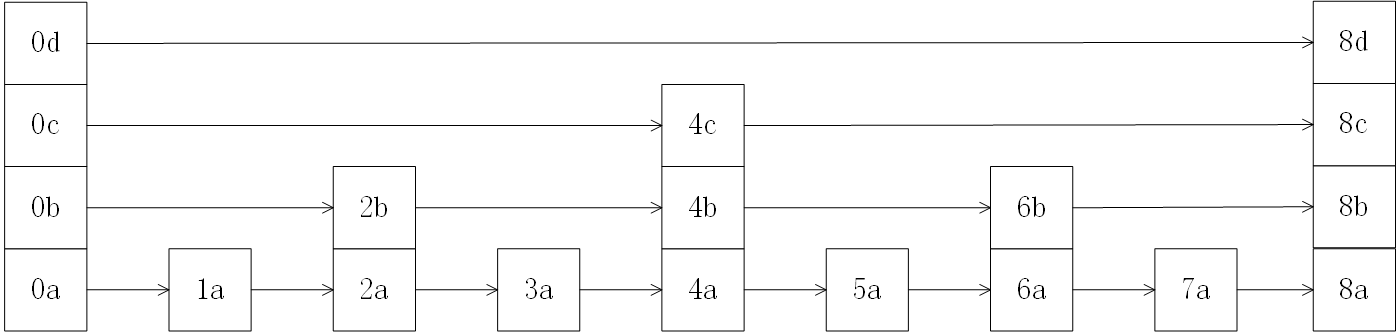
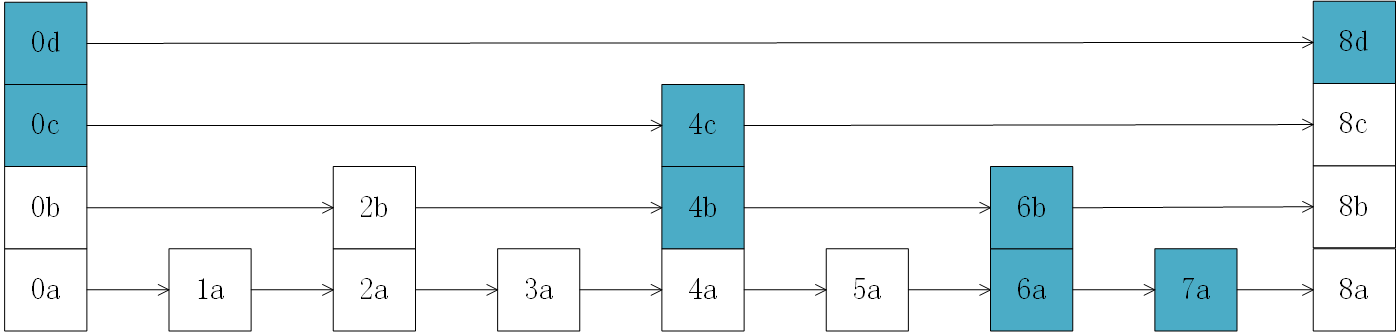
实际的跳表
如何确定“层”的高度?
/**
* 获取随机的层高度
* @return
*/
private int getRandomHeight() {
Random random = new Random();
int i = 1;
for (; i
为什么时间复杂度平均O(logN),最坏O(N)?
节点的分值
跳跃表的插入-代码实现
public SkipListNode slInsert(double score, T obj) {
int levelHeight = getRandomHeight();
SkipListNode
下一篇:2 - Java入门