Acwing 843. n-皇后问题
2021-02-02 03:15
阅读:395
n-皇后问题是指将 n 个皇后放在 n∗n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
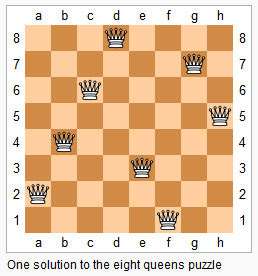
现在给定整数n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数n。
输出格式
每个解决方案占n行,每行输出一个长度为n的字符串,用来表示完整的棋盘状态。
其中”.”表示某一个位置的方格状态为空,”Q”表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
数据范围
1≤n≤91≤n≤9
输入样例:
4
输出样例:
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
第一种解法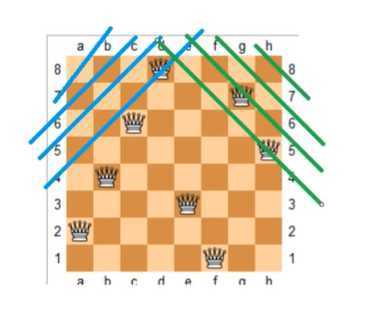
思路:如上图,只需要判断列,左斜线(y = -x + b --> b = x + y)和右斜线(y = x + b--> b = y - x)三种情况,其中b(截距)就是我们的在格子的位置
1 #include2 3 using namespace std; 4 5 const int N = 20; 6 int n; 7 char g[N][N]; 8 bool col[N],dg[N],udg[N]; 9 10 void dfs(int y){ 11 if(n == y){ 12 for(int i = 0;i ) puts(g[i]); 13 puts(""); 14 return; 15 } 16 17 for(int i = 0;i ){ 18 if(col[i] == 0 && dg[n + y - i] == 0 && udg[ y + i] == 0){ 19 g[y][i] = ‘Q‘; 20 col[i] = dg[n + y - i] = udg[y + i] = true; 21 dfs(y + 1); 22 g[y][i] = ‘.‘; 23 col[i] = dg[n + y - i] = udg[y + i] = false; 24 } 25 } 26 27 } 28 29 int main(){ 30 scanf("%d",&n); 31 for(int i = 0;i ) 32 for(int j = 0;j ) 33 g[i][j] = ‘.‘; 34 dfs(0); 35 return 0; 36 }
第二种解法
思路:每一个格子有放还是不放两种情况,顺次判断,时间复杂度n^2
1 // 2 #include3 4 using namespace std; 5 6 const int N = 20; 7 int n; 8 char g[N][N]; 9 bool row[N],col[N],dg[N],udg[N]; 10 11 void dfs(int x,int y,int s){ 12 if(y == n) y = 0,x++;//如果出界就转回来 13 14 if(x == n){//枚举到最后一行 15 //这里有可能皇后不够 16 if(s == n){//如果摆放的皇后等于n,说明找到了一组解 17 for(int i = 0;i "%s\n",g[i]); 18 puts(""); 19 } 20 return; 21 } 22 //枚举格子的两种选择 23 //第一种是不放皇后 24 dfs(x,y+1,s);//直接递归到下一个格子就可以了 25 26 //第二种是放皇后 27 if(!row[x] && !col[y] && !dg[n + x - y] && !udg[x + y]){ 28 g[x][y] = ‘Q‘; 29 row[x] = col[y] = dg[n + x - y] = udg[x + y] = true; 30 dfs(x,y + 1,s + 1); 31 row[x] = col[y] = dg[n + x - y] = udg[x + y] = false; 32 g[x][y] = ‘.‘; 33 } 34 } 35 36 int main(){ 37 scanf("%d",&n); 38 for(int i = 0;i ) 39 for(int j = 0;j ) 40 g[i][j] = ‘.‘; 41 dfs(0,0,0);//从左上角开始搜索 42 return 0; 43 }
评论
亲,登录后才可以留言!