python实现线性回归之弹性网回归
2021-02-02 10:17
标签:determine alt tail weixin call pre plink main ant 弹性网回归是lasso回归和岭回归的结合,其代价函数为: 若令 由此可知,弹性网的惩罚系数 上述解释摘自:https://blog.csdn.net/weixin_41500849/article/details/80447501 接下来是实现代码,代码来源: https://github.com/eriklindernoren/ML-From-Scratch 首先还是定义一个基类,各种线性回归都需要继承该基类: 然后是弹性网回归的核心: 接着是弹性网回归的代码: 其中涉及到的一些函数可参考:https://www.cnblogs.com/xiximayou/p/12802868.html 最后是运行主函数: 结果: Mean squared error: 11.232800207362782 (given by reg. factor: 0.05) python实现线性回归之弹性网回归 标签:determine alt tail weixin call pre plink main ant 原文地址:https://www.cnblogs.com/xiximayou/p/12808904.html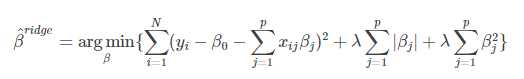
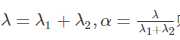 ,则
,则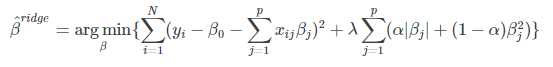
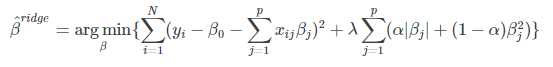
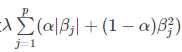 恰好为岭回归罚函数和Lasso罚函数的一个凸线性组合.当α=0时,弹性网回归即为岭回归;当 α=1时,弹性网回归即为Lasso回归.因此,弹性网回归兼有Lasso回归和岭回归的优点,既能达到变量选择的目的,又具有很好的群组效应。
恰好为岭回归罚函数和Lasso罚函数的一个凸线性组合.当α=0时,弹性网回归即为岭回归;当 α=1时,弹性网回归即为Lasso回归.因此,弹性网回归兼有Lasso回归和岭回归的优点,既能达到变量选择的目的,又具有很好的群组效应。class Regression(object):
""" Base regression model. Models the relationship between a scalar dependent variable y and the independent
variables X.
Parameters:
-----------
n_iterations: float
The number of training iterations the algorithm will tune the weights for.
learning_rate: float
The step length that will be used when updating the weights.
"""
def __init__(self, n_iterations, learning_rate):
self.n_iterations = n_iterations
self.learning_rate = learning_rate
def initialize_weights(self, n_features):
""" Initialize weights randomly [-1/N, 1/N] """
limit = 1 / math.sqrt(n_features)
self.w = np.random.uniform(-limit, limit, (n_features, ))
def fit(self, X, y):
# Insert constant ones for bias weights
X = np.insert(X, 0, 1, axis=1)
self.training_errors = []
self.initialize_weights(n_features=X.shape[1])
# Do gradient descent for n_iterations
for i in range(self.n_iterations):
y_pred = X.dot(self.w)
# Calculate l2 loss
mse = np.mean(0.5 * (y - y_pred)**2 + self.regularization(self.w))
self.training_errors.append(mse)
# Gradient of l2 loss w.r.t w
grad_w = -(y - y_pred).dot(X) + self.regularization.grad(self.w)
# Update the weights
self.w -= self.learning_rate * grad_w
def predict(self, X):
# Insert constant ones for bias weights
X = np.insert(X, 0, 1, axis=1)
y_pred = X.dot(self.w)
return y_pred
class l1_l2_regularization():
""" Regularization for Elastic Net Regression """
def __init__(self, alpha, l1_ratio=0.5):
self.alpha = alpha
self.l1_ratio = l1_ratio
def __call__(self, w):
l1_contr = self.l1_ratio * np.linalg.norm(w)
l2_contr = (1 - self.l1_ratio) * 0.5 * w.T.dot(w)
return self.alpha * (l1_contr + l2_contr)
def grad(self, w):
l1_contr = self.l1_ratio * np.sign(w)
l2_contr = (1 - self.l1_ratio) * w
return self.alpha * (l1_contr + l2_contr)
class ElasticNet(Regression):
""" Regression where a combination of l1 and l2 regularization are used. The
ratio of their contributions are set with the ‘l1_ratio‘ parameter.
Parameters:
-----------
degree: int
The degree of the polynomial that the independent variable X will be transformed to.
reg_factor: float
The factor that will determine the amount of regularization and feature
shrinkage.
l1_ration: float
Weighs the contribution of l1 and l2 regularization.
n_iterations: float
The number of training iterations the algorithm will tune the weights for.
learning_rate: float
The step length that will be used when updating the weights.
"""
def __init__(self, degree=1, reg_factor=0.05, l1_ratio=0.5, n_iterations=3000,
learning_rate=0.01):
self.degree = degree
self.regularization = l1_l2_regularization(alpha=reg_factor, l1_ratio=l1_ratio)
super(ElasticNet, self).__init__(n_iterations,
learning_rate)
def fit(self, X, y):
X = normalize(polynomial_features(X, degree=self.degree))
super(ElasticNet, self).fit(X, y)
def predict(self, X):
X = normalize(polynomial_features(X, degree=self.degree))
return super(ElasticNet, self).predict(X)
from __future__ import print_function
import matplotlib.pyplot as plt
import sys
sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/")
import numpy as np
import pandas as pd
# Import helper functions
from mlfromscratch.supervised_learning import ElasticNet
from mlfromscratch.utils import k_fold_cross_validation_sets, normalize, mean_squared_error
from mlfromscratch.utils import train_test_split, polynomial_features, Plot
def main():
# Load temperature data
data = pd.read_csv(‘mlfromscratch/data/TempLinkoping2016.txt‘, sep="\t")
time = np.atleast_2d(data["time"].values).T
temp = data["temp"].values
X = time # fraction of the year [0, 1]
y = temp
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
poly_degree = 13
model = ElasticNet(degree=15,
reg_factor=0.01,
l1_ratio=0.7,
learning_rate=0.001,
n_iterations=4000)
model.fit(X_train, y_train)
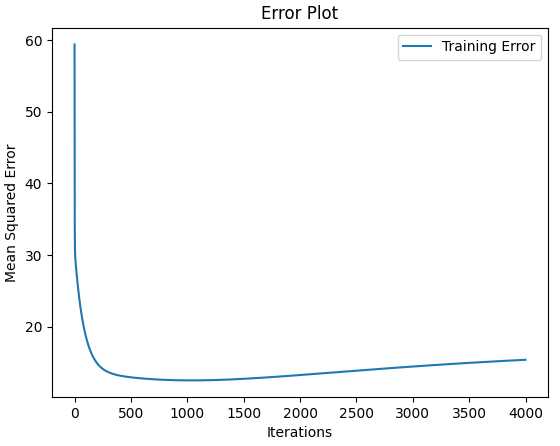
# Training error plot
n = len(model.training_errors)
training, = plt.plot(range(n), model.training_errors, label="Training Error")
plt.legend(handles=[training])
plt.title("Error Plot")
plt.ylabel(‘Mean Squared Error‘)
plt.xlabel(‘Iterations‘)
plt.savefig("test1.png")
plt.show()
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print ("Mean squared error: %s (given by reg. factor: %s)" % (mse, 0.05))
y_pred_line = model.predict(X)
# Color map
cmap = plt.get_cmap(‘viridis‘)
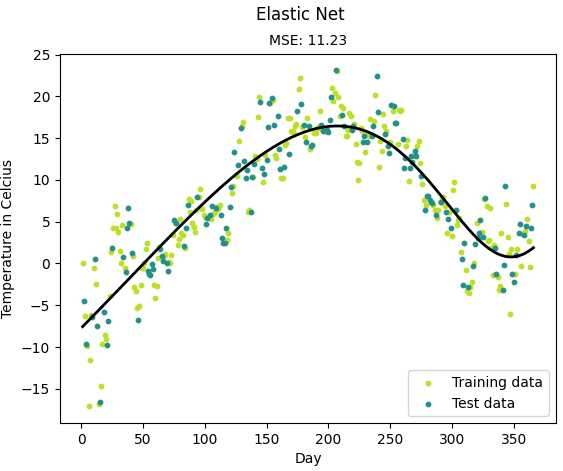
# Plot the results
m1 = plt.scatter(366 * X_train, y_train, color=cmap(0.9), s=10)
m2 = plt.scatter(366 * X_test, y_test, color=cmap(0.5), s=10)
plt.plot(366 * X, y_pred_line, color=‘black‘, linewidth=2, label="Prediction")
plt.suptitle("Elastic Net")
plt.title("MSE: %.2f" % mse, fontsize=10)
plt.xlabel(‘Day‘)
plt.ylabel(‘Temperature in Celcius‘)
plt.legend((m1, m2), ("Training data", "Test data"), loc=‘lower right‘)
plt.savefig("test2.png")
plt.show()
if __name__ == "__main__":
main()
上一篇:java读取配置文件