标签:图片 main 思想 ber log and 展开 问题 class
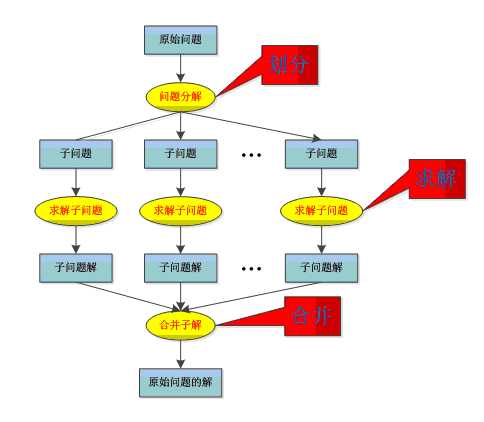
分治算法思想
将问题分为k个子问题,对这k个子问题分别求解。如果子问题的规模仍然不够小,则每个子问题再划分为k个子问题,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止。
问题分析
这个问题的时间复杂度我似懂非懂,想知道其中的具体过程的请自行百度。
对于两个数字X、Y,传统计算方式的时间复杂度是O(n^2)。
那么我们可以根据高位低位进行分隔,例如:

其中,xn0、xn1分别为A、B的位数,yn0、yn1同理。那么X*Y可写成如下结果:
\[\begin{align}
X*Y &= (A*10^{xn1}+B)(C*10^{yn1}+D)\ &= AC*10^{xn1+yn1}+AD*10^{xn1}+BC*10^{yn1}+BD
\end{align}
\]
由于我们需要计算4次大整数乘积,所以算法复杂度依然时O(n^2)。
为了减小时间复杂度,我们进行如下改动:
令:
\[ABCD = (A*10^{xn1}-B)(D-C*10^{yn1})
\]
展开可得:
\[ABCD = AD*10^{xn1}-AC*10^{xn1+yn1}-BD+BC*10^{yn1}
\]
综上可得:
\[X*Y = ABCD+2AC*10^{xn1+yn1}+2BD
\]
现在我们将时间复杂度降低到了O(n^1.59)。
C++代码
#include
#include
typedef long long ll;
using namespace std;
void AcceptAndCompute();
int SizeNumber(ll num);
ll Compute(ll X, ll Y, int xn, int yn);
int Sign(ll x);
int main()
{
AcceptAndCompute();
return 0;
}
void AcceptAndCompute()
{
ll X, Y;
cout>X;
cout>Y;
cout 0 ? 1 : -1;
}
ll Compute(ll X, ll Y, int xn, int yn)
{
if(!X || !Y) return 0;
if(xn == 1 || yn == 1) return X * Y;
int xn0 = xn / 2, yn0 = yn / 2;
int xn1 = xn - xn0, yn1 = yn - yn0;
ll A = ll(X / ll(pow(10, xn1)));
ll B = ll(X % ll(pow(10, xn1)));
ll C = ll(Y / ll(pow(10, yn1)));
ll D = ll(Y % ll(pow(10, yn1)));
ll AC = Compute(A, C, xn0, yn0);
ll BD = Compute(B, D, xn1, yn1);
ll ABCD = Compute(ll(A*pow(10,xn1)-B), ll(D-C*pow(10, yn1)), xn0, yn0);
return ll(2*AC*pow(10, (xn1+yn1))+ABCD+2*BD);
}
感谢
分治法的经典问题——大整数相乘
大整数乘法-分治算法
标签:图片 main 思想 ber log and 展开 问题 class
原文地址:https://www.cnblogs.com/xxmmqg/p/12807158.html

