「解题报告」 [JSOI2019] 节日庆典 (扩展kmp)
2021-02-04 08:14
标签:mes image 报告 space ini c++ 前缀 inf ret 传送门 给定一个字符串 \(s\) (起始位置为 \(1\)), 对 \(s\) 的每个前缀求出最小循环表示的起始位置. \(|s| \le 3 \times 10^6\). 假设先从前往后扫一遍, 则对于每个前缀, 它的某些后缀可以作为最优答案 (我们称它为有效的), 有些后缀可以被排除. 并且我们可以证明 : 对于每个前缀, 它的有效后缀数量为 \(O(\log n)\). 我们规定 : 以一个前缀的结束位置来命名这个前缀, 以一个后缀的起始位置来命名这个后缀. \(|i|\) 表示后缀 \(i\) 的长度. 对于前缀 \(R\), 我们把它的有效后缀按照起始位置从小到大排序, 设 \(i,j\) 为它的两个相邻有效后缀. 因为它们都有可能得到最优答案, 所以后缀 \(j\) 是后缀 \(i\) 的一个前缀. 有因为后缀 \(j\) 是后缀 \(i\) 的一个后缀, 所以后缀 \(j\) 是后缀 \(i\) 的一个 \(border\). (图中蓝括号部分和红括号部分对应相等) 所以, 后缀 \(i\) 可以用一个长度为 \(j-i\) 的字符串循环表示. (图中箭头所指部分对应相等) 设 \(k=j+(j-i)\) 假设 \(j\) 是前缀 \(R\) 的最优解, 那么就会存在两个点 \(S,T(T-S=j-i)\), 使得字符串 \([i,S] >\) 字符串 \([j,T]\). (图中分别表示为 \(I,J\)) 由于字符串 \(A,B\) 对应相等, 所以字符串 \(C>D\). 那么, 也就会使得字符串 \([j,S] > [k,T]\). (图中分别表示为 \(J‘,K\)) 也就是说, \(k\) 会代替 \(j\) 成为前缀 \(R\) 的最优解, 那 \(j\) 就不是一个「有效后缀」, 与假设矛盾. 故, 对于前缀 \(R\) 的两个相邻有效后缀 \(i,j\), 必定满足 \(|i| \ge |j|\). 所以前缀 \(R\) 最多只会有 \(\log R\) 个有效后缀. 首先是找出有效后缀. 我们从前往后枚举 \(R\), 并维护一个栈来存储当前的有效后缀, 具体见代码. 然后是找出这若干个有效后缀中的最优解. 对于两个有效后缀 \(i,j\ (i 「解题报告」 [JSOI2019] 节日庆典 (扩展kmp) 标签:mes image 报告 space ini c++ 前缀 inf ret 原文地址:https://www.cnblogs.com/BruceW/p/13143857.html「解题报告」 [JSOI2019] 节日庆典 (扩展kmp)
题面
题意
输入样例
abaacaba
输出样例
1 1 3 3 3 6 3 8
数据范围
思路
证明

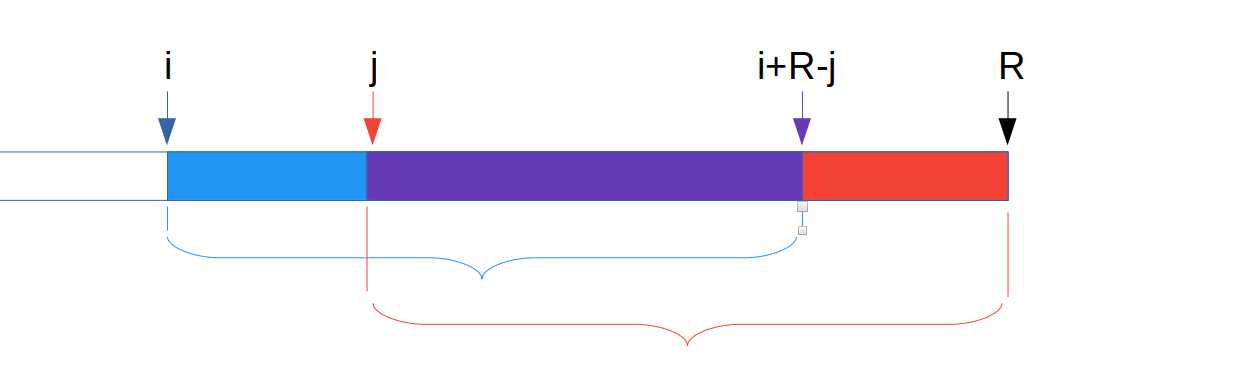
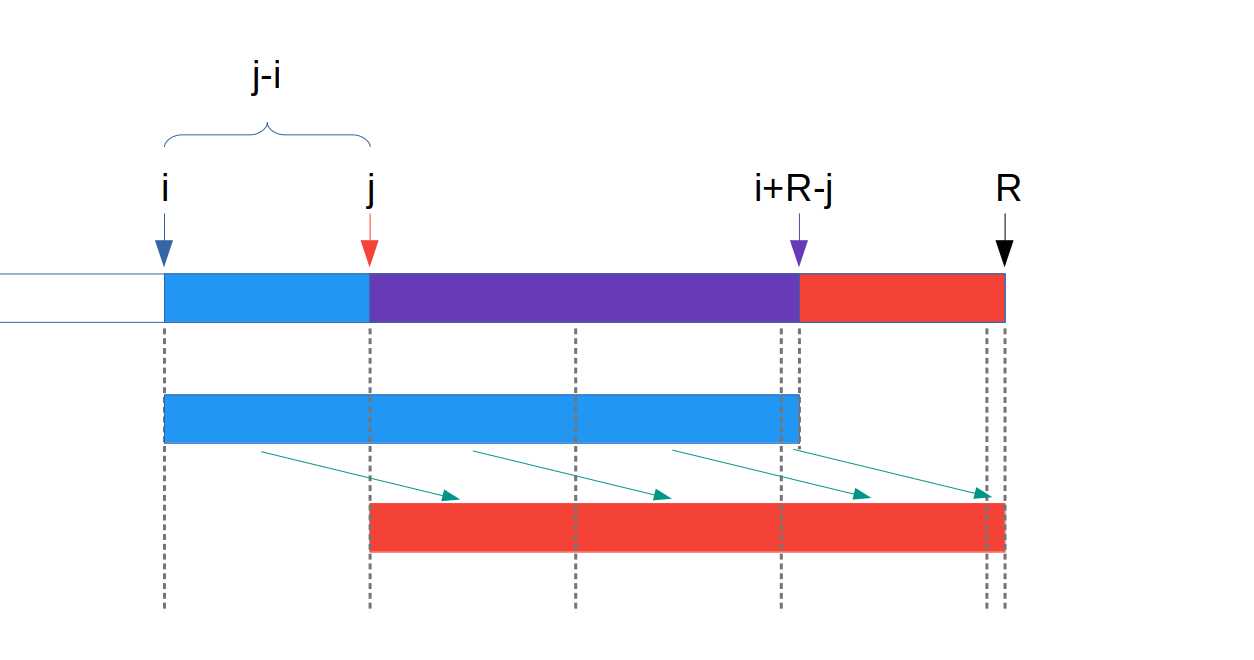
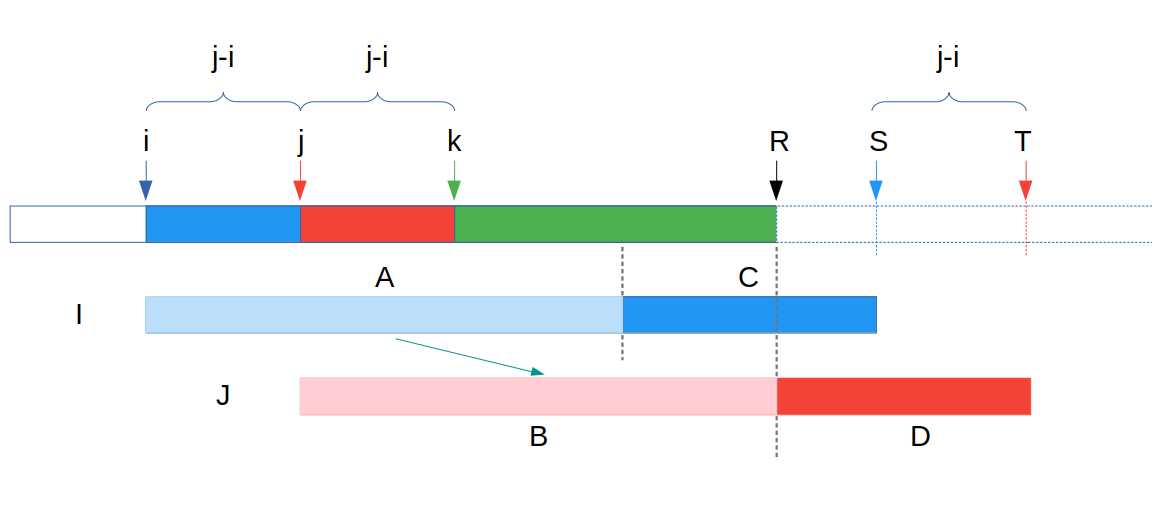
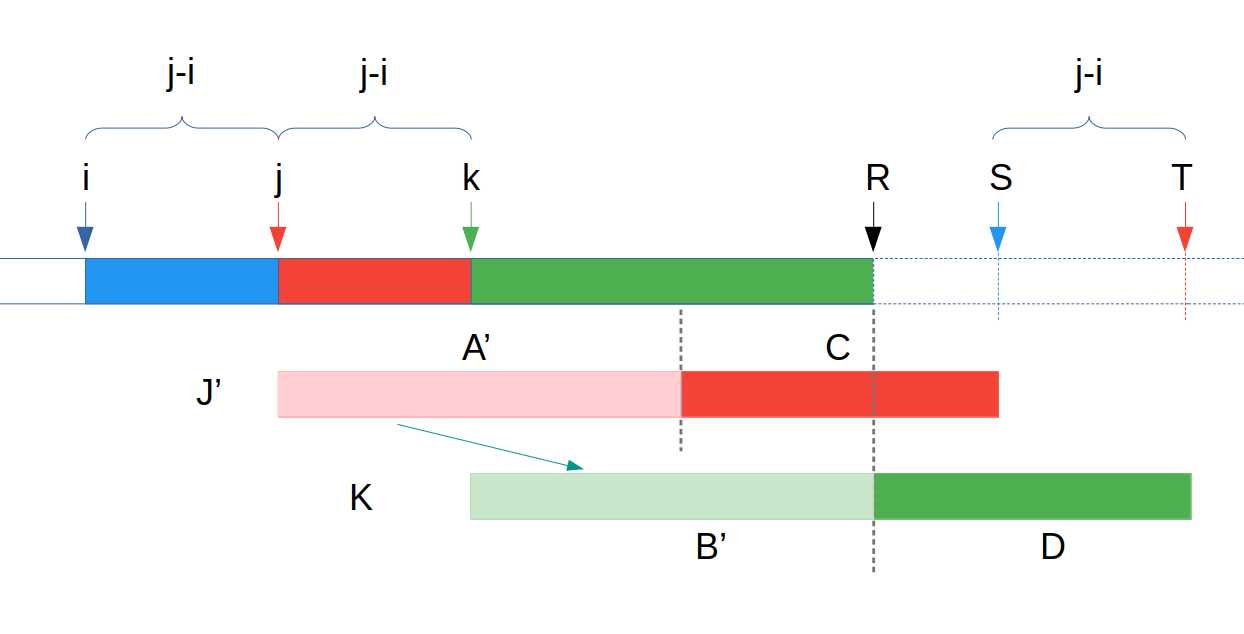
具体实现
代码
#include
文章标题:「解题报告」 [JSOI2019] 节日庆典 (扩展kmp)
文章链接:http://soscw.com/essay/50806.html