[POJ3417]Network/闇の連鎖
2021-02-06 17:16
标签:nbsp 题目 状态 struct rda 差分 tchar return 能力 传说中的暗之连锁被人们称为 Dark。 Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。经过研究,你发现 Dark 呈现无向图的结构,图中有 N 个节点和两类边,一类边被称为主要边,而另一类被称为附加边。 Dark 有 N – 1条主要边,并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。另外,Dark 还有 M 条附加边。你的任务是把 Dark 斩为不连通的两部分。一开始 Dark的附加边都处于无敌状态,你只能选择一条主要边切断。一旦你切断了一条主要边,Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。但是你的能力只能再切断 Dark 的一条附加边。现在你想要知道,一共有多少种方案可以击败 Dark。注意,就算你第一步切断主要边之后就已经把 Dark 斩为两截,你也需要切断一条附加边才算击败了 Dark 第一行包含两个整数 N 和 M。 输出一个整数表示答案 4 1 3 这是一道树上差分 锯题可知,首先将主要边构成一棵树,如果再将附加边(x,y)加入则会构成一个环,所以不能这样; 如果第一次选择切断主要边,那么第二步就要切断附加边; 所以,我们可以将附加边(x,y)两点的路径覆盖主要边的次数统计出来; 1。如果,主要边被覆盖了零次,那么说明,任何一条附加边与这条边切断都可以分成两部分; 2。如果,主要边被覆盖了一次,那么说明,只有一条附加边与这条边切断都可以分成两部分; 3。如果,主要边被覆盖了两次,那么说明,这条边切断后不能分成两部分; 具体如图: (黑色代表主要边,红色代表附加边) 然后,我们可以求出,两个附件边的点,的最近公共祖先; 将最近公共祖先点上的权值减2,将两个点的权值加1;如图二所示; 为什么是这样加减呢; 我们知道 一个数组 x-y的权值加 d,就相当于 它的差分数组的 a[x]+d , a[y+1]-d (不知道的,自己上网搜) 那么,这是每一次覆盖次数加一,然后每个点都和公共祖先有一条边,所以最近公共祖先点上的权值减2,将两个点的权值加1; 树上差分还是有点区别的,这样理解就好了; 然后定义f[x],代表以x为根节点,的所有子节点,包括自己的权值和; 那么f[x]就表示,x与它父节点之间的边的覆盖次数; 最后,如果f[x]==0,ans+=m(m代表附加边的数量) 如果f[x]==1,,ans++ 要注意的是,f[x] 如果x是1(根节点),答案ans不需要改变 [POJ3417]Network/闇の連鎖 标签:nbsp 题目 状态 struct rda 差分 tchar return 能力 原文地址:https://www.cnblogs.com/wzx-RS-STHN/p/13110564.html题目
Description
Input
之后 N – 1 行,每行包括两个整数 A 和 B,表示 A 和 B 之间有一条主要边。
之后 M 行以同样的格式给出附加边。
N≤100 000,M≤200 000。数据保证答案不超过 2^31 – 1Output
Sample Input
1 2
2 3
1 4
3 4Sample Output
思路:
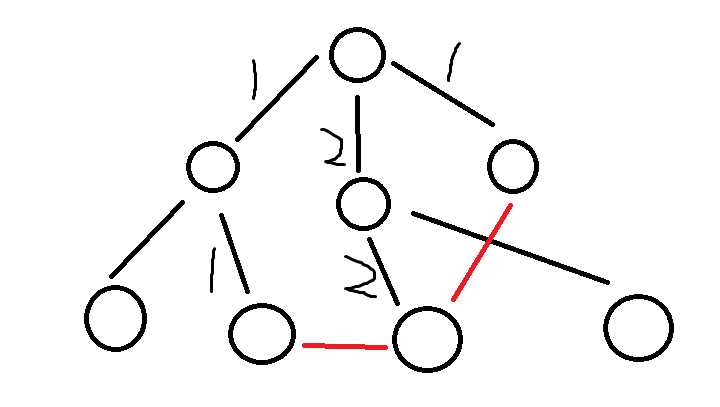
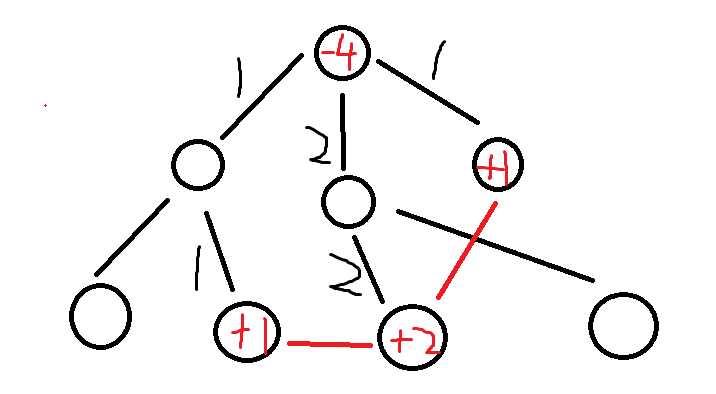
代码
#include
上一篇:【网络】一文说清HTTPS