数据结构与算法-二叉排序树
2021-02-08 21:18
标签:图片 int 查找 temp @param info 判断 src search 二叉排序树:BST,对于二叉排序树的任何一个非叶子结点,要求左子结点的值比当前结点的值小,右子结点的值比当前结点的值大 特别说明:若有相同的值,可以将该结点放在左子结点或右子结点 删除有以下三种情况 第一种情况,删除叶子结点 第二种情况,删除只有一颗子树的结点 先找到要删除的结点 targetNode 找到要删除结点的父结点 parent 判断要删除结点的子结点是左子结点还是右子结点 targetNode的孩子 判断要删除结点是其父结点的左子结点还是右子结点 targetNode 和 parent 若要删除的结点有左孩子 targetNode 的孩子 若要删除的结点是其父结点的左孩子 targetNode 是 parent的左孩子时 parent.left = targetNode.left; 若要删除的结点是其父结点的右孩子 targetNode 是 parent的右孩子时 parent.right = targetNode.right; 第三种情况,删除有两颗子树的结点 数据结构与算法-二叉排序树 标签:图片 int 查找 temp @param info 判断 src search 原文地址:https://www.cnblogs.com/yfyyy/p/12769540.html二叉排序树
1. 基本介绍
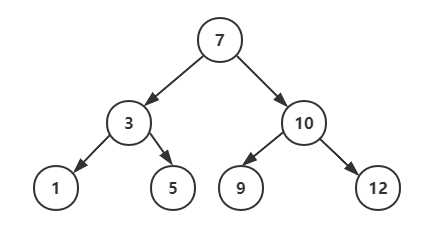
2. 二叉排序树的创建和遍历
public void add(Node node) {
if(node == null) {
return;
}
if(node.value 3. 二叉排序树的删除
/**
* 查找要删除的结点
* @param value 希望删除结点的值
* @return 如果找到,返回该结点否则返回null
*/
public Node search(int value) {
if(value == this.value) { //就是此结点,找到
return this;
}else if(value = this.value && this.right != null) {
return this.right.searchParent(value); //向右子树递归查找
}else {
return null;
}
}
}
// 删除结点
public void delNode(int value) {
if (root != null) {
// 1.需求先去找到要删除的结点 targetNode
Node targetNode = search(value);
// 如果没有找到要删除的结点
if (targetNode == null) {
return;
}
// 如果我们发现当前这颗二叉排序树只有一个结点
if (root.left == null && root.right == null) {
root = null;
return;
}
// 去找到targetNode的父结点
Node parent = searchParent(value);
// 如果要删除的结点是叶子结点
if (targetNode.left == null && targetNode.right == null) {
// 判断targetNode 是父结点的左子结点,还是右子结点
if (parent.left != null && parent.left.value == value) { // 是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {// 是由子结点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
targetNode.value = delRightTreeMin(targetNode.right);
} else { // 删除只有一颗子树的结点
// 如果要删除的结点有左子结点
if (targetNode.left != null) {
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { // 如果要删除的结点有右子结点
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.right;
} else { // 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//查找要删除的结点
public Node search(int value) {
if(root == null) {
return null;
}else {
return root.search(value);
}
}
//查找父结点
public Node searchParent(int value) {
if(root == null) {
return null;
}else {
return root.searchParent(value);
}
}
上一篇:c++中的new