八大排序之选择类排序
2021-02-18 18:17
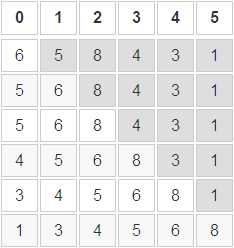
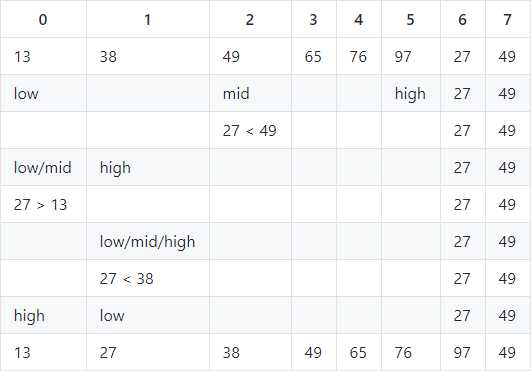
标签:分代 解析 else https 移动 插入 log 存储空间 直接 对序列:6,5,8,4,3,1 进行直接插入排序 由直接插入排序代码,选取最内层 作为基本操作语句 综上所述,本算法的平均时间复杂度O(n^2) 对序列:13,38,49,65,76,97,27,49进行一趟折半插入排序。 前6个元素已经排好序列,查找27的插入位置 同直接插入排序,O(1) 将待排序列分成几个子序列,分别对这几个子序列进行直接插入排序 如果增量是1,那么就是直接插入排序 先将要排序的一组数按某个增量d分成若干组,每组中记录的下标相差d 对每组中全部元素进行排序,然后再用一个较小的增量对它进行,在每组中再进行排序 当增量减到1时,整个要排序的数被分成一组,排序完成 增量序列的最后一个值一定取1 增量序列中的值尽量没有除1之外的公因子 八大排序之选择类排序 标签:分代 解析 else https 移动 插入 log 存储空间 直接 原文地址:https://www.cnblogs.com/YC-L/p/12689017.html直接插入排序
示例
int main()
{
int a[10] = { 6,5,8,4,3,7 };
int temp, j;
for (int i = 1; i 6; ++i){
temp = a[i];
for (j = i - 1; j >= 0 && temp j){
a[j + 1] = a[j];
}
a[j + 1] = temp;
}
j = 0;
while (j 6){
printf("%d", a[j]);
++j;
}
return 0;
}
时间复杂度分析
a[j + 1] = a[j];
空间复杂度分析
折半插入排序
示例
int main()
{
// a[0]为存储临时变量的位置
int a[9] = { 0, 13, 38, 49, 65, 76, 97, 27, 49 };
int low, high, mid;
for (int i = 2; i 8; ++i){
a[0] = a[i];
low = 1;
high = i - 1;
while (low high){
mid = (low + high) / 2;
if (a[mid] > a[0]){
high = mid - 1;
}
else{
low = mid + 1;
}
}
for (int j = i - 1; j >= high + 1; --j){
a[j + 1] = a[j];
}
a[high + 1] = a[0];
}
int j = 0;
while (j 8){
printf("%d ", a[j]);
++j;
}
return 0;
}
时间复杂度分析
空间复杂度分析
希尔排序(缩小增量排序)
该方法实质上是一种分组插入方法
算法思想
示例

void ShellSort(int r[],int n){
int i,j,d;
int x;
d=n/2;//d=n>>1
while(d>=1){
for(i=d ;i
希尔排序不稳定
时间复杂度
空间复杂度O(1)
上一篇:python2.7安装pip