GaussianElimination 高斯消去法java(求逆,求解)
2021-02-19 09:21
标签:col back span -- ati int() 退出 ext str 题目 GaussianElimination 高斯消去法java(求逆,求解) 标签:col back span -- ati int() 退出 ext str 原文地址:https://www.cnblogs.com/shish/p/12685396.htmljava代码
import java.util.Scanner;
public class GaussianElimination{
public static void Input(int n, double[][] A, double[] b, int length){
Scanner in = new Scanner(System.in);
System.out.println("输入方程组的系数矩阵A;");
for (int i = 0; i ) {
for (int j = 0; j ) {
A[i][j] = in.nextDouble();
}
}
if(length == 1){
System.out.println("输入方程组矩阵b:");
for (int i = 0; i ) {
b[i] = in.nextDouble();
}
}
}
public static void Merge1(int n, double[][] A, double[] b){
for (int i = 0; i ) {
A[i][n] = b[i];
}
Print(n, A, 1);
return;
}
public static void Merge2(int n, double[][] A){
for (int i = 0; i ) {
for (int j = n; j ) {
A[i][j] = 0;
}
A[i][n+i] = 1;
}
Print(n, A, n);
return;
};
public static void Print(int n, double[][] A, int length){
System.out.println("##################手 动 分 割 线#####################");
System.out.println("增广矩阵:");
for (int i = 0; i ) {
for (int j = 0; j ) {
System.out.printf("%-11.4f", A[i][j]);
}
System.out.print("\n");
}
} //length为1,求逆为n
public static void Swap(int n, double[][]A, int i, int pivotrow, int length){
double temp = 0;
for (int k = 0; k ) {
temp = A[i][k];
A[i][k] = A[pivotrow][k];
A[pivotrow][k] = temp;
}
} //交换行
public static int SelectPivotrow(int n, double[][]A, int i) {
int pivotrow = i;
for (int j = i + 1; j ) {
if (Math.abs(A[j][i]) > Math.abs(A[pivotrow][i]))
pivotrow = j;
}
if (A[pivotrow][i] == 0)
return -1;
else
return pivotrow;
} //选择主元
public static void ForwardElimination(int n, double[][]A, int length){
for (int i = 0; i ) {
int pivotrow = SelectPivotrow(n, A, i);
if(pivotrow == -1){
System.out.println("输出结果不唯一");
break;
}
Swap(n, A, i, pivotrow, length);
for (int j = i+1; j ) {
double temp = A[j][i]/A[i][i];
for (int k = i; k ) {
A[j][k] = A[j][k] - A[i][k] * temp;
}
}
Print(n, A, length);
}
} //前向消去,求length为1,求逆为n
public static void BackElimination(int n, double[][]A, int length){
for (int i = n-1; i > 0; i--) {
for (int j = i-1; j >= 0; j--) {
double temp = A[j][i]/A[i][i];
for (int k = n+length-1; k > j; k--) {
A[j][k] = A[j][k] - A[i][k] * temp;
}
}
Print(n, A, length);
}
} //反向替换,求length为1,求逆为n
public static void Normalization(int n, double[][]A, int length){
for (int i = 0; i ) {
for (int j = n; j ) {
A[i][j] = A[i][j]/A[i][i];
}
A[i][i] = 1;
}
Print(n, A, length);
} //归一化,length为1,求逆为n
public static void PrintResult(int n, double[][] A, int length){
System.out.println("##################手 动 分 割 线#####################");
System.out.println("最终结果为:");
if(length == 1){
for (int i = 0; i ) {
System.out.println("x"+(i+1)+" = "+A[i][n+length-1]);
}
}
else if(n == length){
System.out.println("矩阵的逆:");
for (int i = 0; i ) {
for (int j = n; j ) {
System.out.printf("%-11.2f", A[i][j]);
}
System.out.print("\n");
}
}
return ;
}
public static void Do(int n, double[][]A, int length){
ForwardElimination(n, A, length);
BackElimination(n, A, length);
Normalization(n, A, length);
PrintResult(n, A, length);
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while(true){
System.out.println("-----------------高 斯 消 元 法------------------");
System.out.println("求逆矩阵请输入1,求解请输入2,退出请输入0。");
int flag = in.nextInt();
if(flag != 0){
System.out.println("输入方程组的元数:");
int n = in.nextInt();
double[][] A = new double[n][2*n];
double[] b = new double[n];
double[] x = new double[n];
double[][] A_I = new double[n][n];
if(flag ==1){
Input(n, A, b, n);
Merge2(n, A);
Do(n, A, n);
}else{
Input(n, A, b ,1);
Merge1(n, A, b);
Do(n, A,1);
}
}else break;
}
System.out.println("-----------------程 序 结 束 !!------------------");
}
}
结果:
求解
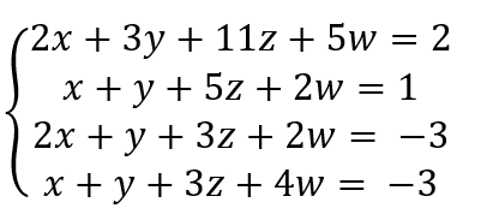
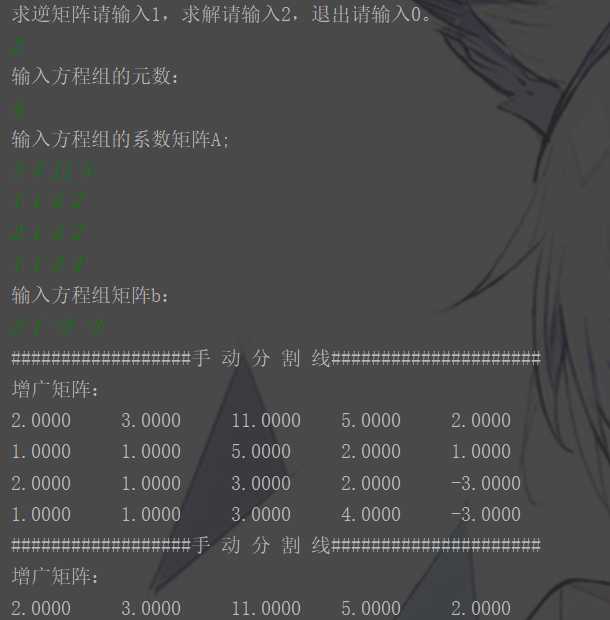
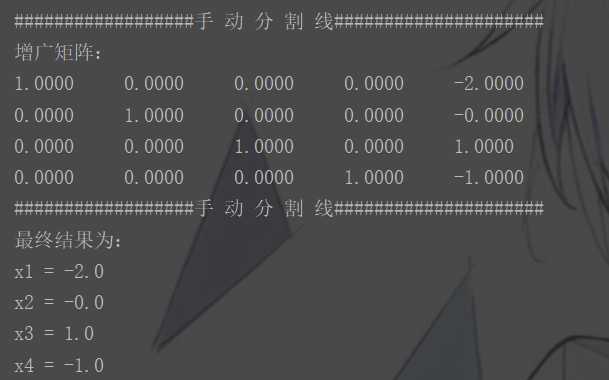
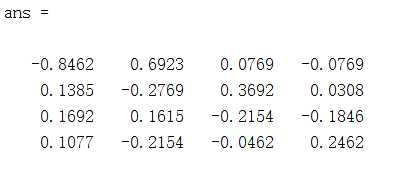
求逆

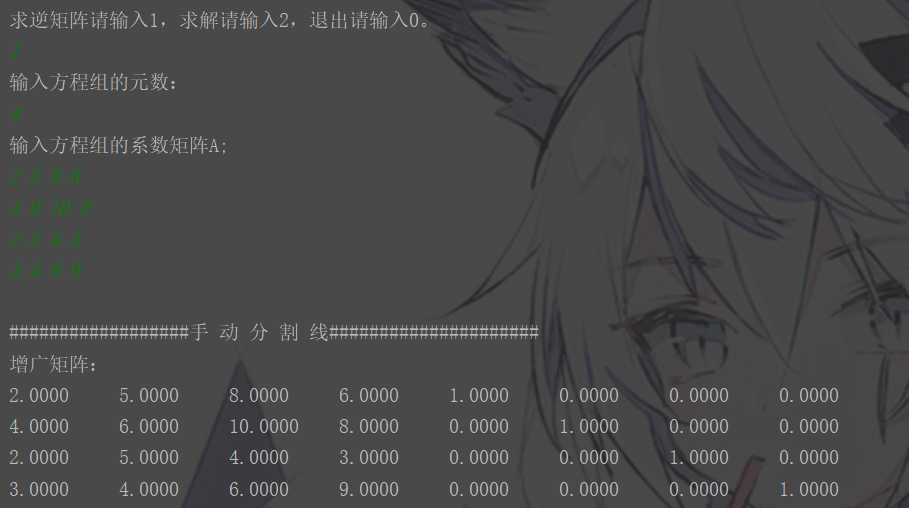
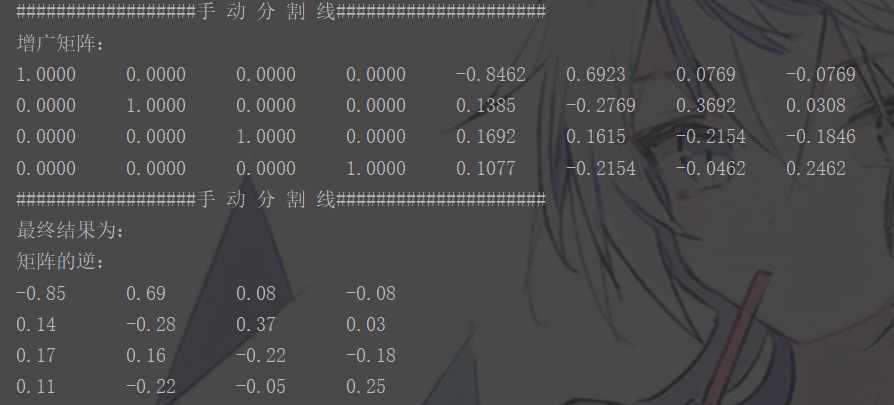
上一篇:如何新建一个jar包库?
文章标题:GaussianElimination 高斯消去法java(求逆,求解)
文章链接:http://soscw.com/essay/57471.html