排序算法之归并排序
2021-02-20 21:22
标签:排序算法 时间 cpp bsp 空间 oid for 分解 结束 分治法: 将原问题分解为几个规模较小但类似于原问题的子问题,递归得求解这些子问题,然后再合并这些子问题的解 来建立原问题的解。即遵循3个步骤: 分解:将原问题分解为规模较小的若干实例。 解决:递归求解各个子问题。然而,若子问题的规模足够小,则直接求解。 合并:将子问题的解合并成原问题的解。 归并排序描述: 归并排序完全遵从分治模式。直观上其操作如下: 分解:分解待排序的n个元素的序列成各具n/2个元素的两个子序列。 解决:使用归并排序递归地排序两个子序列。 合并:合并两个已排序的子序列产生答案。 当待排序的序列长度为1时,递归开始回升,在这种情况下不要做任何工作。 以一个大小为8的数组为例进行归并排序,其过程如下: 如橙色箭头所示,勾画出程序执行时递归栈(从左向右)的情况,当一个结点的左右子问题都执行结束时,调用merge函数。 算法实现: 算法时间复杂度分析: 递归和合并操作都是与n有关的函数,而且能构造递归树,所以采用递归式求解。 整个代码的复杂度为:T(n) = 2 * T(n/2) + O(n),然后通过展开求解 如:T(n/2) = 2 * T(n/4) + O(n/2), 上面两式合并:T(n) = 2 * [ 2 * T(n/4) + O(n/2) ] + O(n) = 22 * T(n/4) + 2 * O(n) 由于递归树一共有lgn层。 所以:T(n) = 2lgn * T(1) + lgn * O(n) = nlgn 排序算法之归并排序 标签:排序算法 时间 cpp bsp 空间 oid for 分解 结束 原文地址:https://www.cnblogs.com/yanghh/p/12678758.html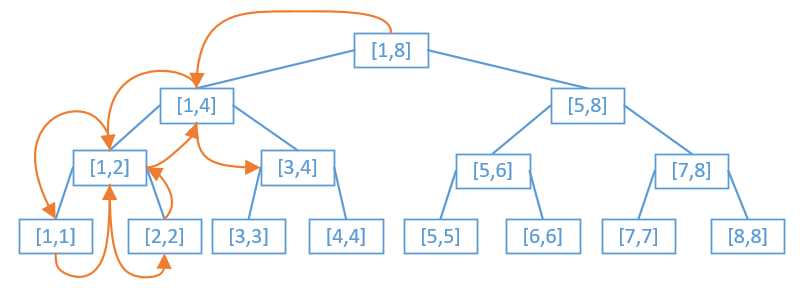
int extra[N]; // 需要额外的空间
void merge(int low, int mid, int high)
{
for(int i = low; i