贪心算法:根据身高重建队列(续集)
2021-03-08 14:27
标签:效率 定义 释放 拷贝 经典 地方 pos iter 代码 ? 但是在解释的过程中有不恰当的地方,所以来专门写一篇文章来详细说一说这个问题。 使用vector的代码如下: 耗时如下: 这么一分析好像和版本二链表实现的时间复杂度是一样的啊,为什么提交之后效率会差距这么大呢? 耗时如下: 使用链表 对于动态数组,就是可以不用关心初始时候的大小,可以随意往里放数据,那么耗时的原因就在于动态数组的底层实现。 动态数组为什么可以不受初始大小的限制,可以随意push_back数据呢? 「首先vector的底层实现也是普通数组」。 vector的大小有两个维度一个是size一个是capicity,size就是我们平时用来遍历vector时候用的,例如: 而capicity是vector底层数组(就是普通数组)的大小,capicity可不一定就是size。 当insert数据的时候,如果已经大于capicity,capicity会成倍扩容,但对外暴漏的size其实仅仅是+1。 那么既然vector底层实现是普通数组,怎么扩容的? 就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!) 举一个例子,如图: 原vector中的size和capicity相同都是3,初始化为1 2 3,此时要push_back一个元素4。 那么底层其实就要申请一个大小为6的普通数组,并且把原元素拷贝过去,释放原数组内存,「注意图中底层数组的内存起始地址已经变了」。 「同时也注意此时capicity和size的变化,关键的地方我都标红了」。 而在贪心算法:根据身高重建队列中,我们使用vector来做insert的操作,此时大家可会发现,*「虽然表面上复杂度是O(n^2),但是其底层都不知道额外做了多少次全量拷贝了,所以算上vector的底层拷贝,整体时间复杂度可以认为是O(n^2 + t n)级别的,t是底层拷贝的次数」**。 那么是不是可以直接确定好vector的大小,不让它在动态扩容了,例如在贪心算法:根据身高重建队列中已经给出了有people.size这么多的人,可以定义好一个固定大小的vector,这样我们就可以控制vector,不让它底层动态扩容。 这种方法需要自己模拟插入的操作,不仅没有直接调用insert接口那么方便,需要手动模拟插入操作,而且效率也不高! 手动模拟的过程其实不是很简单的,需要很多细节,我粗略写了一个版本,如下: 耗时如下: vector手动模拟insert 但这份代码在leetcode上统计的耗时甚至比版本一的还高,我们都不让它动态扩容了,为什么耗时更高了呢? 一方面是leetcode的耗时统计本来就不太准,忽高忽低的,只能测个大概。 另一方面:可能是就算避免的vector的底层扩容,但这个固定大小的数组,每次向后移动元素赋值的次数比方法一中移动赋值的次数要多很多。 因为方法一中一开始数组是很小的,插入操作,向后移动元素次数比较少,即使有偶尔的扩容操作。而方法三每次都是按照最大数组规模向后移动元素的。 所以对于两种使用数组的方法一和方法三,也不好确定谁优,但一定都没有使用方法二链表的效率高! 一波分析之后,对于贪心算法:根据身高重建队列 ,大家就安心使用链表吧!别折腾了,哈哈,相当于我替大家折腾了一下。 总结 如果抛开语言谈算法,除非从来不用代码写算法纯分析,「否则的话,语言功底不到位O(n)的算法可能写出O(n^2)的性能」,哈哈。 相信在这里学习算法的录友们,都是想在软件行业长远发展的,都是要从事编程的工作,那么一定要深耕好一门编程语言,这个非常重要! 「代码随想录」一直都是技术公众号里的一抹清流,值得介绍给身边的朋友同学们! 打算从头开始打卡的录友,可以在「算法汇总」这里找到历史文章,很多录友都在从头打卡,你并不孤单! -------end------- 我将算法学习相关的资料已经整理到了Github :https://github.com/youngyangyang04/leetcode-master,里面还有leetcode刷题攻略、各个类型经典题目刷题顺序、思维导图看一看一定会有所收获,如果给你有帮助给一个star支持一下吧! 贪心算法:根据身高重建队列(续集) 标签:效率 定义 释放 拷贝 经典 地方 pos iter 代码 原文地址:https://blog.51cto.com/15069438/2576186
通知:一些录友表示经常看不到每天的文章,现在公众号已经不按照发送时间推荐了,而是根据一些规则乱序推送,所以可能关注了「代码随想录」也一直看不到文章,建议把「代码随想录」设置星标哈,设置星标之后,每天就按发文时间推送了,Carl每天都是定时8:35发送的,嗷嗷准时!
在讲解贪心算法:根据身高重建队列中,我们提到了使用vector(C++中的动态数组)来进行insert操作是费时的。// 版本一,使用vector(动态数组)
class Solution {
public:
static bool cmp(const vector
其直观上来看数组的insert操作是O(n)的,整体代码的时间复杂度是O(n^2)。// 版本二,使用list(链表)
class Solution {
public:
// 身高从大到小排(身高相同k小的站前面)
static bool cmp(const vector
大家都知道对于普通数组,一旦定义了大小就不能改变,例如int a[10];,这个数组a至多只能放10个元素,改不了的。
for (int i = 0; i 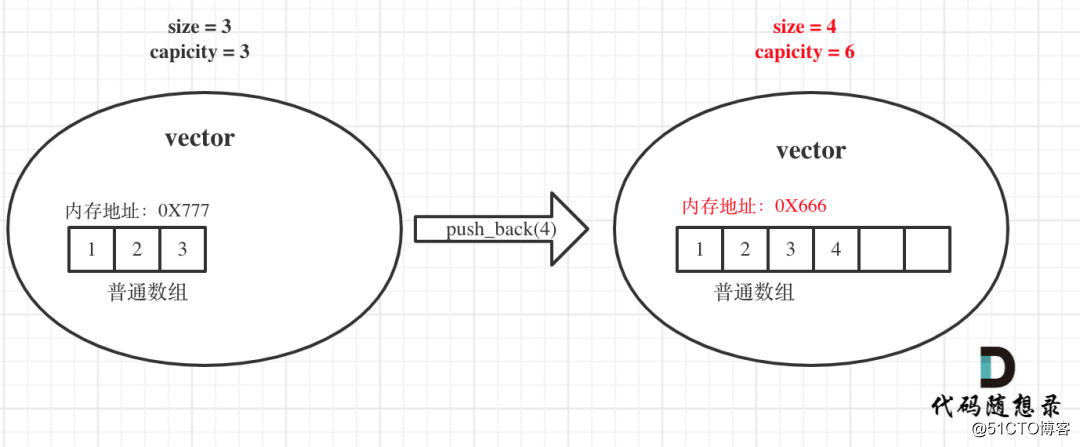
// 版本三
// 使用vector,但不让它动态扩容
class Solution {
public:
static bool cmp(const vector
这份代码就是不让vector动态扩容,全程我们自己模拟insert的操作,大家也可以直观的看出是一个O(n^2)的方法了。
大家应该发现了,编程语言中一个普通容器的insert,delete的使用,都可能对写出来的算法的有很大影响!
上一篇:本周小结!(贪心算法系列三)
下一篇:贪心算法:用最少数量的箭引爆气球