贪心算法:无重叠区间
2021-03-08 14:28
标签:更新 ems 理解 复杂度 ppi 最大 inter seo 分割线 **? 给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。 注意: 示例 1: 示例 2: 示例 3: 思路 这其实是一个难点! 按照右边界排序,就要从左向右遍历,因为右边界越小越好,只要右边界越小,留给下一个区间的空间就越大,所以从左向右遍历,优先选右边界小的。 按照左边界排序,就要从右向左遍历,因为左边界数值越大越好(越靠右),这样就给前一个区间的空间就越大,所以可以从右向左遍历。 如果按照左边界排序,还从左向右遍历的话,要处理各个区间右边界的各种情况。 一些同学做这道题目可能真的去模拟去重复区间的行为,这是比较麻烦的,还要去删除区间。 题目只是要求移除区间的个数,没有必要去真实的模拟删除区间! 「我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了」。 此时问题就是要求非交叉区间的最大个数。 右边界排序之后,局部最优:优先选右边界小的区间,所以从左向右遍历,留给下一个区间的空间大一些,从而尽量避免交叉。全局最优:选取最多的非交叉区间。 局部最优推出全局最优,试试贪心! 这里记录非交叉区间的个数还是有技巧的,如图: 每次取非交叉区间的时候,都是可右边界最小的来做分割点(这样留给下一个区间的空间就越大),所以第一条分割线就是区间1结束的位置。 接下来就是找大于区间1结束位置的区间,是从区间4开始。「那有同学问了为什么不从区间5开始?别忘已经是按照右边界排序的了」。 区间4结束之后,在找到区间6,所以一共记录非交叉区间的个数是三个。 总共区间个数为6,减去非交叉区间的个数3。移除区间的最小数量就是3。 C++代码如下: 总结 总结如下难点: 一些录友可能看网上的题解代码很简单,照葫芦画瓢稀里糊涂的就过了,但是其题解可能并没有把问题难点讲清楚,然后自己再没有钻研的话,那么一道贪心经典区间问题就这么浪费掉了。 贪心就是这样,代码有时候很简单(不是指代码短,而是逻辑简单),但想法是真的难! 这和动态规划还不一样,动规的代码有个递推公式,可能就看不懂了,而贪心往往是直白的代码,但想法读不懂,哈哈。 「所以Carl把本题的难点也一一列出,帮大家不仅代码看的懂,想法也理解的透彻!」 循序渐进学算法,认准「代码随想录」就够了,值得介绍给身边的朋友同学们! 贪心算法:无重叠区间 标签:更新 ems 理解 复杂度 ppi 最大 inter seo 分割线 原文地址:https://blog.51cto.com/15069438/2576183
通知:一些录友基础比较薄弱,不知道从哪里开始刷题。可以看一下公众号左下角的「算法汇总」,「算法汇总」已经把题目顺序编排好了,文章顺序即刷题顺序,这是全网最详细的刷题顺序了,方便录友们从头打卡学习,「算法汇总」会持续更新!
题目链接:https://leetcode-cn.com/problems/non-overlapping-intervals/
可以认为区间的终点总是大于它的起点。
区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1 解释: 移除 [1,3] 后,剩下的区间没有重叠。
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
「相信很多同学看到这道题目都冥冥之中感觉要排序,但是究竟是按照右边界排序,还是按照左边界排序呢?」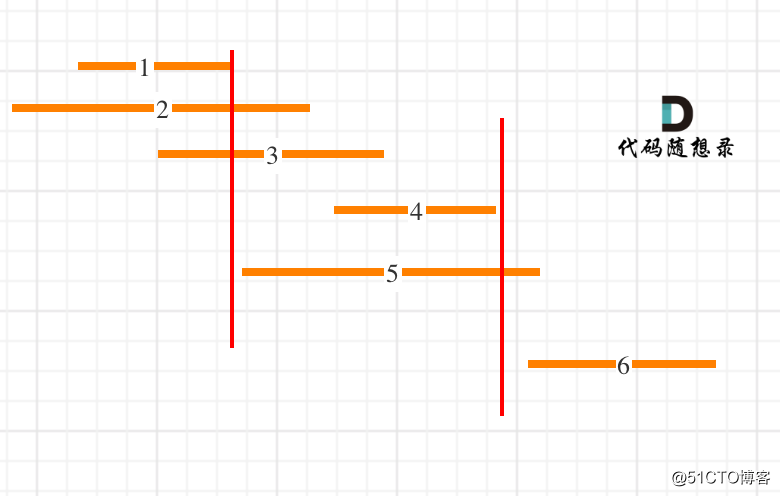
435.无重叠区间
区间,1,2,3,4,5,6都按照右边界排好序。
class Solution {
public:
// 按照区间右边界排序
static bool cmp (const vector
大家此时会发现如此复杂的一个问题,代码实现却这么简单!
本题我认为难度级别可以算是hard级别的!
「这四个难点都不好想,但任何一个没想到位,这道题就解不了」。