[校招-基础算法]常见的ML、DL编程题
2021-03-10 20:32
标签:plot def list section intersect 类别 统计量 负数 进制 在算法岗的面试中,除了数据结构和算法的编程题外,机器学习/深度学习的编程题也常常用来考察候选人的基础能力。不能讲了一大堆天花乱坠的算法,连个简单的算法都不能独立实现。 NMS用来去掉重复的框。输入前面得到的框,对于每一类,按照score进行降序排序,最大的那个一定保留,然后和其他的框计算IOU。IOU大于一定阈值视为重复的框,丢弃掉。 训练阶段,求均值和方差时,在N、H、W上操作,而保留通道 C 的维度。具体来说,就是把第1个样本的第1个通道,加上第2个样本第1个通道 ...... 加上第 N 个样本第1个通道,求平均,得到通道 1 的均值(注意是除以 N×H×W 而不是单纯除以 N,最后得到的是一个代表这个 batch 第1个通道平均值的数字,而不是一个 H×W 的矩阵)。 BN在测试阶段使用的统计量不是在一个batch上计算的,而是整个数据集上的,可以用移动平均法求得。 计算均值和标准差时,把每一个样本 feature map 的 channel 分成 G 组,每组将有 C/G 个 channel,然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。多用于检测分割等占用显存较大的任务。 下面是简易版本的实现。 注意,np.random.randint()是取值范围是左闭右开区间,python自带的random.randint()是闭区间。 首先,什么是上溢出和下溢出?实数在计算机内用二进制表示,不是一个精确值。 当数值过小的时候,被四舍五入为0,这就是下溢出。此时如果除以它就会出问题。(也有说法指超出所能表示的最小数字时是下溢出)。 有个方法可以同时解决上溢出和下溢出的问题: 求所有z中的最大值max_z,然后求 这两种曲线是评价分类模型performance的常用方法。其中,PR图的纵坐标是precision,横坐标是recall;ROC曲线的纵坐标是True Positive Rate,横坐标是False Positive Rate。它们的公式如下: 实现的代码如下: 扫码添加微信,一定要备注研究方向+地点+学校+昵称(如机器学习+上海+上交+汤姆),只有备注正确才可以加群噢。 [校招-基础算法]常见的ML、DL编程题 标签:plot def list section intersect 类别 统计量 负数 进制 原文地址:https://blog.51cto.com/15054042/2564168非极大值抑制(NMS)
import numpy as np
def nms(dets, thresh):
x1 = dets[:, 0] # bbox top_x
y1 = dets[:, 1] # bbox top_y
x2 = dets[:, 2] # bbox bottom_x
y2 = dets[:, 3] # bbox bottom_y
scores = dets[:, 4] # 分类score
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
order = scores.argsort()[::-1] # 按score做降序排序
keep = []
while order.size > 0:
i = order[0]
keep.append(i)
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
intersection = w * h
iou = intersection / (areas[i] + areas[order[1:]] - intersection)
inds = np.where(iou Batch Normalization
import numpy as np
def batch_rorm(x, gamma, beta):
# x_shape:[N, C, H, W]
results = 0.
eps = 1e-5
x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
x_var = np.var(x, axis=(0, 2, 3), keepdims=True)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
return resultsGroup Normalization
import numpy as np
def group_norm(x, gamma, beta, G=16):
# x_shape:[N, C, H, W]
results = 0.
eps = 1e-5
x = np.reshape(x, (x.shape[0], G, x.shape[1]//G, x.shape[2], x.shape[3]))
x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
x_var = np.var(x, axis=(2, 3, 4), keepdims=True)
x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
results = gamma * x_normalized + beta
results = np.reshape(results, (results.shape[0], results.shape[1]*results.shape[2], results.shape[3], results.shape[4]))
return resultsKmeans聚类
import numpy as np
import random
def kmeans(data, k):
m = len(data) # 样本个数
n = len(data[0]) # 维度
cluster_center = np.zeros((k, n)) # k个聚类中心
# 选择合适的初始聚类中心
# 在已有数据中随机选择聚类中心
# 也可以直接用随机的聚类中心
init_list = np.random.randint(low=0, high=m, size=k) # [0, m)
for index, j in enumerate(init_list):
cluster_center[index] = data[j][:]
# 聚类
cluster = np.zeros(m, dtype=np.int) - 1 # 所有样本尚未聚类
cc = np.zeros((k, n)) # 下一轮的聚类中心
c_number = np.zeros(k) # 每个簇样本的数目
for times in range(1000):
for i in range(m):
c = nearst(data[i], cluster_center)
cluster[i] = c # 第i个样本归于第c簇
c_number[c] += 1
cc[c] += data[i]
for i in range(k):
cluster_center[i] = cc[i] / c_number[i]
cc.flat = 0
c_number.flat = 0
return cluster
def nearst(data, cluster_center):
nearst_center_index = 0
dis = np.sum((cluster_center[0] - data) ** 2)
for index, center in enumerate(cluster_center):
dis_temp = np.sum((center - data) ** 2)
if dis_temp softmax
import numpy as np
def convert_label_to_onehot(classes, labels):
"""
classes: 类别数
labels: array,shape=(N,)
"""
return np.eye(classes)[labels].T
def softmax(logits):
"""logits: array, shape=(N, C)"""
res = np.zeros_like(logits)
for i, row in enumerate(logits):
exp_sum = np.sum(np.exp(row))
for j, val in enumerate(row):
res[i,j] = np.exp(val)/ exp_sum
return res
if __name__ == ‘__main__‘:
# 有四个样本,有三个类别
logits = np.array([[0, 0.45, 0.55],
[0.9, 0.05, 0.05],
[0.4, 0.6, 0],
[1, 0, 0]])
pred = np.argmax(softmax(logits), axis=1)
print(pred)softmax的上、下溢出问题
当数值过大超出所能表示的最大正数时,就会发生上溢出。
如对于一个数组 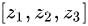 求softmax,
求softmax,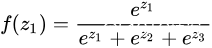 ,如果 某个
,如果 某个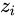 非常大,那么
非常大,那么 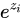 将会非常大,有可能上溢出;当所有
将会非常大,有可能上溢出;当所有 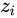 都非常小(绝对值很大的负数),求指数之后会接近于0,就有可能下溢出。
都非常小(绝对值很大的负数),求指数之后会接近于0,就有可能下溢出。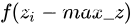 即可,这样肯定不会有上溢出的风险,同时由于在分母上肯定有一个1,因此也不会有下溢出的风险。
即可,这样肯定不会有上溢出的风险,同时由于在分母上肯定有一个1,因此也不会有下溢出的风险。PR曲线和ROC曲线的绘制
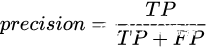 ,
,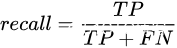 ,
,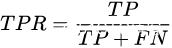 ,
,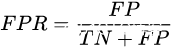 .
.import numpy as np
import matplotlib.pyplot as plt
data_number = 50
labels = np.random.randint(0, 2, size=data_number) # 真实的类别
scores = np.random.choice(np.arange(0.1, 1, 0.01), data_number) # 模型判断样本为类别1的置信度
def pr_curve(y, pred):
pos = np.sum(y == 1)
neg = np.sum(y == 0)
pred_sort = np.sort(pred)[::-1]
index = np.argsort(pred)[::-1]
y_sort = y[index]
print(y_sort)
pre = []
rec = []
for i, item in enumerate(pred_sort):
if i == 0:
pre.append(1)
rec.append(0)
else:
pre.append(np.sum((y_sort[:i] == 1)) / i)
rec.append(np.sum((y_sort[:i] == 1)) / pos)
# 画图
plt.plot(rec, pre, ‘k‘)
# plt.legend(loc=‘lower right‘)
plt.title(‘PR curve‘)
plt.plot([(0, 0), (1, 1)], ‘r--‘)
plt.xlim([-0.01, 1.01])
plt.ylim([-0.01, 01.01])
plt.ylabel(‘precision‘)
plt.xlabel(‘recall‘)
plt.show()
def roc_curve(y, pred):
pos = np.sum(y == 1)
neg = np.sum(y == 0)
pred_sort = np.sort(pred)[::-1]
index = np.argsort(pred)[::-1]
y_sort = y[index]
print(y_sort)
tpr = []
fpr = []
thr = []
for i, item in enumerate(pred_sort):
tpr.append(np.sum((y_sort[:i] == 1)) / pos)
fpr.append(np.sum((y_sort[:i] == 0)) / neg)
thr.append(item)
# 画图
plt.plot(fpr, tpr, ‘k‘)
plt.title(‘ROC curve‘)
plt.plot([(0, 0), (1, 1)], ‘r--‘)
plt.xlim([-0.01, 1.01])
plt.ylim([-0.01, 01.01])
plt.ylabel(‘True Positive Rate‘)
plt.xlabel(‘False Positive Rate‘)
plt.show()
pr_curve(labels, scores)
roc_curve(labels, scores)

▲长按加群