CF 999E Reachability from the Capital
2021-03-15 06:37
标签:并且 std dfs c++ size include ons als 连接 题意: 在 Berland 有 \(n\) 座城市和 \(m\) 条道路,每条道路连接着一对城市。 Berland 的道路都是单向的 为了能让首都能够到达所有的城市,最少需要新修建多少新道路? 新道路也是单向的 输入的第一行包含三个整数 \(n,m\) 和 \(s\) \((1\le n \le 5000,0\le m \le 5000 , 1\le s \le n)\) ——城市数,道路数和首都所在城市的标号。 城市的标号为 \(1\) ~ \(n\) 对于每对城市 \(u,v\),从 \(u\) 到 \(v\) 最多只能有一条道路。 允许在一对城市之间建造相反方向的道路(即从 \(u\) 到 \(v\) 和从 \(v\) 到 \(u\) )。 输出一个整数——使从首都可以到达所有城市所需的最少新修建道路数。如果从 \(s\) 已经可以到达所有城市,则输出 \(0\)。 样例 1: 例如,您可以添加道路 ( 6, 4 ) , ( 7 , 9 ) , ( 1 , 7 ),以使从 \(s = 1\) 可到达所有城市。 在此样例中,您可以添加道路(5 , 1),(5 , 2),(5 , 3),(5 , 4)中的任何一条,以使可从 \(s = 5\) 到达所有城市。 如果一个强连通分量内的一个点能被 \(s\) 到达,那么强连通分量里所有点都被 \(s\) 到达,所以先缩点 缩完点建完新图,我们看到的基本上就只有这么三种情况的连通块 我们假设这三种情况都不能被 \(s\) 到达 第一种多个入度为0的点,必须要从 \(s\) 往 \(A\) 和 \(C\) 各连一条边才行 第二种一条链,\(s\) 往 \(E\) 连边就行 第三种只有一个入度为 0 的点,那么 \(s\) 往 \(H\) 连边就行 那么这里就发现了规律了,对于一个不能被 \(s\) 所到达的连通块,其所要新加边的数量为其中入度为 0 点的数量 那么就在新图中先从 \(s\) 所在新图中的点开始 dfs 一遍标记掉能到达的点 然后答案就是新图中没被标记过并且入度为 0 的点数 CF 999E Reachability from the Capital 标签:并且 std dfs c++ size include ons als 连接 原文地址:https://www.cnblogs.com/chinesepikaync/p/12438859.html题目描述
输入格式
接下来 \(m\) 行每行包含一条道路连接着一对城市 \(u_i,v_i\) \((1\le u_i,v_i\le n,u_i\ne v_i)\)输出格式
说明/提示
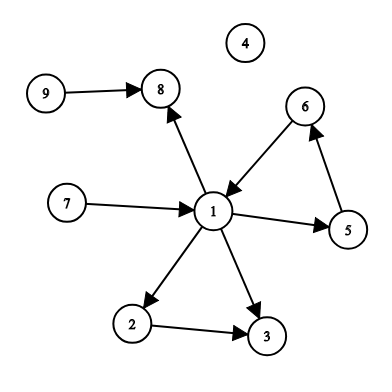
样例 2: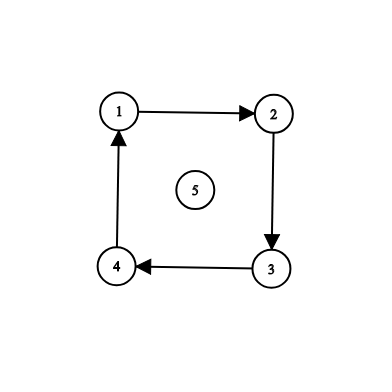
A -> B -> D E -> F -> G H -> I -> J
^ |
| V
C K// This code writed by chtholly_micromaker(MicroMaker)
#include
文章标题:CF 999E Reachability from the Capital
文章链接:http://soscw.com/essay/64844.html