【数据结构与算法】 通俗易懂讲解 二叉搜索树插入删除
2021-03-15 10:35
标签:type code 使用 nod 比较 讲解 mic 代码实现 运行 插入结点的位置对应着查找过程中查找不成功时候的结点位置,因此需要从根结点开始查找带插入结点位置,找到位置后插入即可。下图所示插入结点过程: 插入结点代码如下 二叉搜索树删除结点可以说是二叉搜索树中最为复杂的操作,要考虑的情况比较多,下面分情况讨论。 (2)要删除的结点z为只有一个子树,让z的子树与z的父亲节点相连,删除z即可,删除过程如下图所示: 二叉搜索树删除结点的代码实现如下。 代码中的bstree_successor(z)函数功能是找到结点z的后继结点,至于什么是后继结点以及其实现,前文二叉搜索树查找(请戳我)已有总结,此处不再详述。 上面就是二叉搜索树的插入和删除结点的思路和代码,大家在看代码的时候可以对着图将每种情况在自己脑中运行,比如说对于删除操作的第一种情况,它在代码中的运行流程是什么,这样可能更加容易理解。 【福利】自己搜集的网上精品课程视频分享(上) 码农有道,为您提供通俗易懂的技术文章,让技术变的更简单! 【数据结构与算法】 通俗易懂讲解 二叉搜索树插入删除 标签:type code 使用 nod 比较 讲解 mic 代码实现 运行 原文地址:https://blog.51cto.com/15006953/2552025
二叉搜索树结点定义如下:
typedef struct BSTreeNode{
Type key; // 关键字(键值)
struct BSTreeNode *left; // 左孩子
struct BSTreeNode *right; // 右孩子
struct BSTreeNode *parent; // 父结点
}Node, *BSTree;插入结点
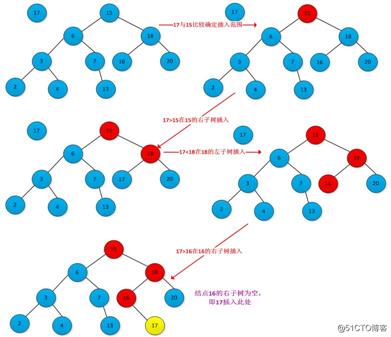
//往树tree的插入结点z
Node* bstree_insert(BSTree tree, Node *z)
{
Node *y = NULL;
Node *x = tree;
// 查找z的插入位置
while (x != NULL)
{
y = x;
if (z->key key)
x = x->left;
else
x = x->right;
}
z->parent = y;
if (y==NULL)
tree = z;
else if (z->key key)
y->left = z;
else
y->right = z;
return tree;
}删除结点
(1)要删除的结点z为叶子结点,这是最简单的一种情况,直接修改其父节点相应指针为NULL。删除过程如下图所示: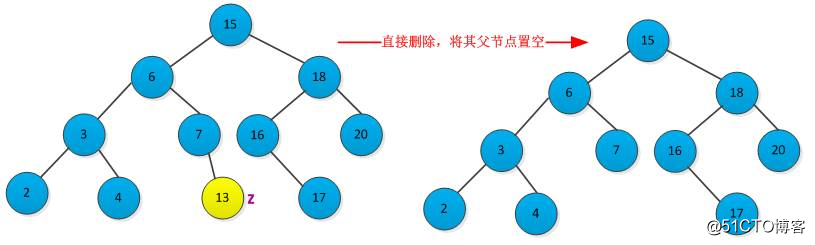
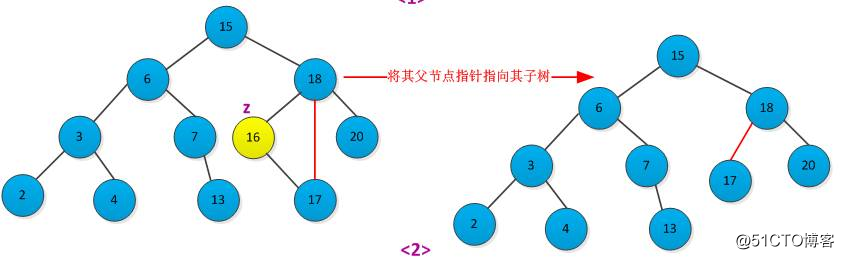
(3)要删除的结点z为有两个子树,则先找到z的后继结点y,y肯定是没有左子树的(如果y还有左子树,那么y就肯定不是z的后继结点),所以现在可以按照上面两种情况删除y结点,最后用y的值代替z的值。整个删除过程如下图所示: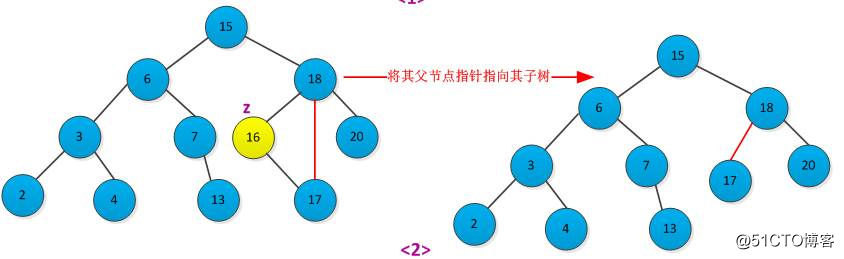
//删除树tree的结点z
Node* bstree_delete(BSTree tree, Node *z)
{
Node *x=NULL;
Node *y=NULL;
if ((z->left == NULL) || (z->right == NULL))
y = z;
else
y = bstree_successor(z);//找到z的后继结点
if (y->left != NULL)
x = y->left;
else
x = y->right;
if (x != NULL)
x->parent = y->parent;
if (y->parent == NULL)
tree = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
if (y != z)
z->key = y->key;
if (y!=NULL)
free(y);
return tree;
}推荐阅读:
【数据结构与算法】 通俗易懂讲解 二叉树遍历
【数据结构与算法】 通俗易懂讲解 二叉搜索树
【数据结构与算法】 通俗易懂讲解 链表
【底层原理】程序局部性原理介绍
【C++札记】C/C++指针使用常见的坑专注服务器后台技术栈知识总结分享
欢迎关注交流共同进步

码农有道 coding