c++中next_permutation()应用
标签:get http rgb res 包含 ++ using ati https
介绍next_permutation()是stl算法库中的方法,主要实现的是用字典序的方法求全排,具体算法后面补写。
下面是几个它的应用场景:
1.凑算式
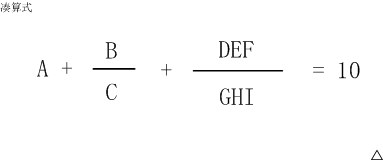
A-G为1-9中各不相同的数,求有多少组合满足上式。
#include
#include
#includeusing namespace std;
int main(){
int x[10];
int i,ans=0;
int a,b,c,d,e;
for(i=0;i9;i++)x[i]=i+1;//next_permutation()是由字典序最小到字典序最大
do{
a=x[0];
b=x[1];
c=x[2];
d=x[3]*100+x[4]*10+x[5];
e=x[6]*100+x[7]*10+x[8];
if(a+(double)b/c+(double)d/e==10.0)ans++;
}while(next_permutation(x,x+9));
coutans;
}
2.带分数(13届蓝桥杯)
100 可以表示为带分数的形式:100 = 3 + 69258 / 714。
还可以表示为:100 = 82 + 3546 / 197。
注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。
类似这样的带分数,100 有 11 种表示法。
输入
从标准输入读入一个正整数N (N1000*1000)
输出
程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
address:https://www.dotcpp.com/oj/problem1440.html
#include
#include
using namespace std;
int getnum(int i,int j,int x[]){
int num=0;
int k,unit=1;
for(k=i;k){
num+=x[k]*unit;
unit*=10;
}
return num;
}
int main(){
int i,j,k,n,ans;
int x[10],a,b,c;
for(i=1;i10;i++)x[i]=i;
ans=0;
cin>>n;
do{
for(i=1;i7;i++){
for(j=i+1;j8;j++){
a=getnum(1,i,x);
b=getnum(i+1,j,x);
c=getnum(j+1,9,x);
if(a+(double)b/c==n)ans++;
}
}
}while(next_permutation(x+1,x+10));
coutans;
return 0;
}
3.排列式问题
7254是一个不寻常的数,因为它可以表示为7254 = 39 x 186,这个式子中1~9每个数字正好出现一次
输出所有这样的不同的式子(乘数交换被认为是相同的式子)
结果小的先输出;结果相同的,较小的乘数较小的先输出。
address:https://www.dotcpp.com/oj/problem1526.html
#include
#include
using namespace std;
int getnum(int i,int j,int x[]){
int k,num=0;
for(k=i;k){
num*=10;
num+=x[k];
}
return num;
}
int main(){
int i,j,a,b,c;
int x[10];
for(i=1;i10;i++)x[i]=i;
do{
for(i=4;i5;i++){
for(j=i+1;j6;j++){
a=getnum(1,i,x);
b=getnum(i+1,j,x);
c=getnum(j+1,9,x);
if(a==c*b)printf("%d = %d x %d\n",a,b,c);
}
}
}while(next_permutation(x+1,x+10));
return 0;
}
c++中next_permutation()应用
标签:get http rgb res 包含 ++ using ati https
原文地址:https://www.cnblogs.com/ydcwp/p/13913429.html
评论
