CSS渐变中是如何定义渐变线的
2021-03-20 01:25
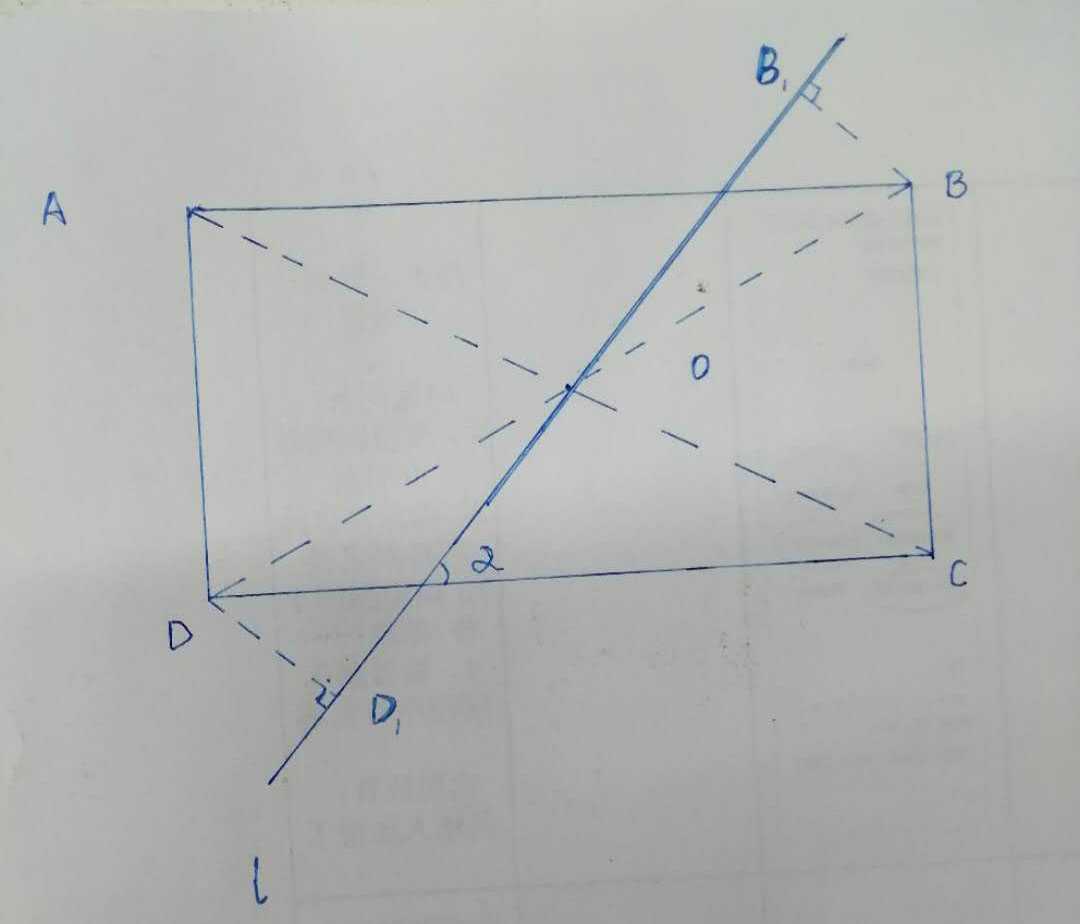
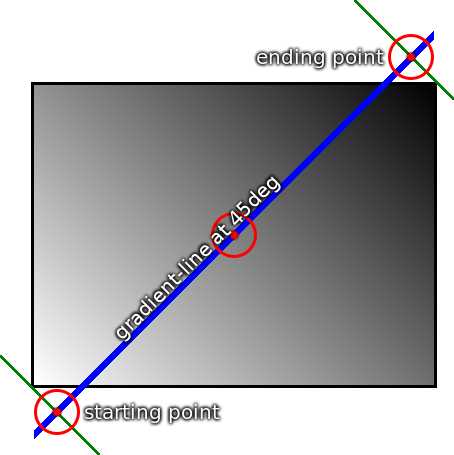
标签:css img 无限 模式 图像 位置 tin 设置 信息 在CSS语法中用户代理对渐变gradient语法的解析渲染离不开渐变线。渐变分为线性渐变(linear gradient)和径向渐变(radial gradient)。 渐变在元素盒模型中background-image属性生成的对应包含块区域创建一个渐变图像。其中线性渐变图像是根据设置的渐变线的角度、色标等参数来渲染生成。 具体来说,元素的线性渐变线是经过元素盒模型的中心点的直线上的线段。该直线按照指定角度进行倾斜,通过背景图像(background-image)包含块区域右上角和左下角作该直线的垂线,两条垂线与该直线的交点组成的线段即为元素线性渐变图像的渐变线。 线性渐变图像中的每一点的颜色与经过该点做渐变线的垂线,垂线与渐变线的交点所拥有的颜色相同。 示例: 为简明清晰说明,这里采用background-repeat:no-repeat模式。矩形ABCD是元素背景图像的生成渐变框区域,O为该矩形的对称中心,直线L为过O点且倾斜角为α的直线,其中α(处于坐标轴一、三象限内)为线性渐变的渐变角度。(注意:定义渐变线方向的角度A(在任何象限中),0度指向上,正角度表示顺时针旋转,所以实际渐变线角度定义的倾斜角度A为90°-α。)过B、D做直线L的垂线,垂足分别为D1、B1。线段D1B1即为计算机在渲染时,计算生成的渐变线。矩形ABCD内任意一点的颜色与过该点作线段D1B1的垂线所形成的交点的点的颜色相同。譬如D与D1点的颜色值相同。 同理类似,若α处于二四象限,就是以A、C作L的垂线,求线性渐变的渐变线。 starting point-起点;ending point-终点 (1)渐变线是图像类别background-image , 不是颜色类别background-color。 本示例从视觉上说明了如何根据上述规则计算渐变线。 这显示了渐变线的起点和终点,以及由背景元素生成的实际渐变:"linear-gradient:(45deg,white,black);"。 请注意,尽管起点和终点不在框的外部,但它们的位置恰好位于右侧,因此渐变在拐角处为纯白色,而在相对拐角处为纯黑色。 这是有意的,并且对于线性渐变永远都是正确的。 注意: A定义渐变线方向的角度(在任何象限中),使0度指向上,正角度表示顺时针旋转, W渐变框的宽度, H渐变框的高度, abs() 返回绝对值的函数, 渐变线的长度(起点和终点之间)为: abs(W*sin(A))+abs(H*cos(A)) 渐变的色标通常放置在渐变线的起点和终点之间,但这不是必需的:渐变线在两个方向上无限延伸。起点和终点仅仅是任意的位置标记,在指定颜色停止时定义0%、0px等位置的起点,而终点定义100%的位置。颜色停止允许在0%之前或100%之后有位置。 线性渐变上任意一点的颜色是找到一条通过该点并且垂直于渐变线的直线来确定的。点的颜色是渐变线在该直线交点的颜色。 线性渐变中渐变线长度公式的证明: 还是根据上面渐变线长度转化的几何题来证明。(A在第1象限时证明) 根据题意有:BD=2OD=√(DC²+BC²),其中DC=W,BC=H。 ∵ sin∠ODD?=OD?/OD 又∵sin∠ODD?=sin(∠BDC+90°-α)=cos(α-∠BDC) ∴OD?/OD=cos(α-∠BDC) OD?/OD=cosαcos∠BDC+sinαsin∠BDC 即OD?=OD[cosαcos∠BDC+sinαsin∠BDC] cos∠BDC=CD/BD,sin∠BDC=BC/BD OD?=OD[cosα*CD/BD+sinα*BC/BD] =0.5Wcosα+0.5Hsinα 而OD?=0.5D?B? 那么D?B?=Wcosα+Hsinα 而A=90°-α 即D?B?=WsinA+HcosA 径向渐变是以渐变椭圆(或圆)的对称中心为起点,以椭圆(或圆)的最外轮廓为终点,按照色标信息绘制的平滑渐变图像。径向渐变在效果上看,就是一圈圈的等比例缩放的同心椭圆(或圆)构成。 参考资料:W3C官网线性渐变linear-gradients https://www.w3.org/TR/css-images-3/#linear-gradients 《CSS+Secret》中文版 P28 CSS渐变中是如何定义渐变线的 标签:css img 无限 模式 图像 位置 tin 设置 信息 原文地址:https://www.cnblogs.com/f6056/p/12746268.html