并查集-二项树与快速合并算法

2021-03-26 00:29

阅读：415

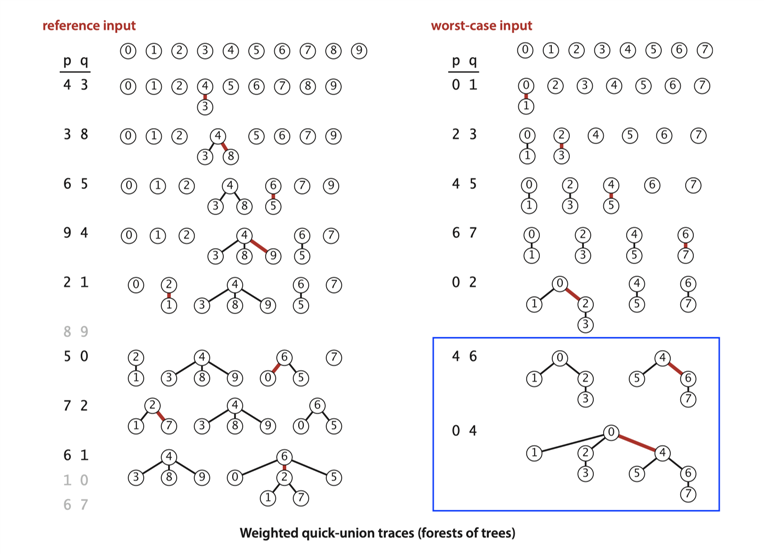
标签：exe lazy lin 图片 time des 倒数 tree prim

ALGS4 Exercise 1.5.15

Problem

Binomial trees. Show that the number of nodes at each level in the worst-case trees for weighted quick-union are binomial coefficients. Compute the average depth of a node in a worst-case tree with \(N = 2^n\) nodes.

Solution

技术图片

从上图中可以看到在 worst-case input 中，

倒数第二行的树，每一层的节点自上而下分别为 1, 2, 1
倒数第一行的树，每一层的节点自上而下分别为 1, 3, 3, 1

符合二项式系数。

对于加权快速合并算法而言，最坏的情况发生在每一次合并中，两棵树具有相同的权值。在这种情况下，每次合并都会造成树的深度增加。

假设合并前的树第 \(i\) 层的节点数为 \(k_{i}\)，合并的后主树这一层的节点数会增加副树第 \(i - 1\) 层的节点数 \(k_{i - 1}\)，即

\[k_{i}^{\prime} = k_{i} + k_{i - 1} \]

因此，所有节点的总深度和就是每一层上每个节点的深度的总和，即

\[\sum_{i = 0}^{n} i \times C_n^i \]

根据 组合数公式，有

\[C_n^r = \frac{n!}{r!(n - r)!} = \frac{n \times (n - 1)!}{r \times (r - 1)!(n - r)!} = \frac{n}{r} \times C_{n - 1}^{r - 1} \]

\[r \times C_n^r = n \times C_{n - 1}^{r - 1} \]

因此，有

\[\sum_{i = 0}^{n} i \times C_n^i = \sum_{i = 1}^{n} n \times C_{n - 1}^{i - 1} \]

根据 二项式公式，有

\[(x + y)^n = \sum_{i = 0}^{n} C_n^i x^{n - i} y^i \]

取 \(x = y = 1\)，可得

\[(x + y)^n = 2^n = \sum_{i = 0}^{n} C_n^i \]

因此，所有节点的总深度之和为

\[\sum_{i = 1}^{n} n \times C_{n - 1}^{i- 1} = n \times \sum_{i = 1}^{n} C_{n - 1}^{i - 1} = n \times 2^{n - 1} \]

平均深度为

\[\frac{n \times 2^{n - 1}}{2^n} = \frac{n}{2} \]

并查集-二项树与快速合并算法

标签：exe lazy lin 图片 time des 倒数 tree prim

原文地址：https://www.cnblogs.com/stO-Orz/p/13762514.html

上一篇：Go语言入门之基础语法&基本数据类型--练气一层

下一篇：通过JavaScript，认识JSON

文章来自：搜素材网的编程语言模块，转载请注明文章出处。
文章标题：并查集-二项树与快速合并算法
文章链接：http://soscw.com/essay/67999.html

亲，登录后才可以留言！

并查集-二项树与快速合并算法

Problem

Solution

评论

热门文章

推荐文章

最新文章

置顶文章