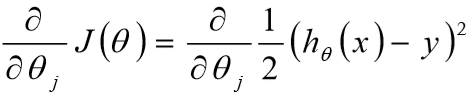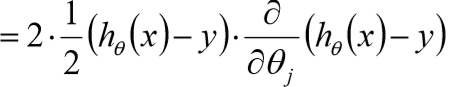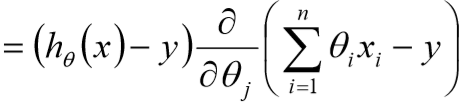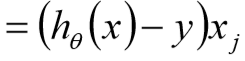记-机器学习(1)-回归算法
2021-03-31 12:26
标签:fun 就是 连续 nbsp idt 梯度下降 线性 作用 最小二乘法 1、什么叫回归算法: 常见的回归算法有: 线性回归、Logistic回归、Softmax回归...... ① 回归算法属于一种有监督学习 ② 回归算法是一种比较常用的机器学习算法,用来建立自变量(x)与因变量(y)之间的关系;从机器学习的角度来讲,用于构建一个算法模型(函数)来做属性(x)与标签(y)之间的映射关系, 在算法的学习过程中,试图寻找一个函数 h: R(d) -> R 使得参数之间的关系拟合性最好 ③ 回归算法中算法(函数)的最终结果是一个连续的数据值,输入值(属性值)是一个d维度的属性/数值量 2、线性回归: 顾名思义,线性回归就是,自变量(x)与因变量(y)之间为线性关系 亦可表示为: 其中, 3、似然函数: 由线性关系公式及误差特性,可推出 可得: 4、对数似然: 5、线性回归的目标函数(损失函数) 6、theta( 最后解出: 7、最小二乘法的参数最优解: ① 参数解析式: ② 最小二乘法的使用要求矩阵 ③ 最小二乘法矩阵逆的求解是一个难点 8、目标函数(loss/cost function): ① ② ③ ④ ⑤ 9、过拟合: 过拟合现象表现为:由于对训练数据的训练准确率过高,导致训练出来的模型在测试数据上的准确率反而下降 10、线性回归的过拟合: ① 目标函数: ② 为了防止数据过拟合,也就是 ③ 正则项(norm): 11、过拟合与正则项 ① L2-norm: ② L1-norm: 12、Ridge回归: 使用L2正则的线性回归模型就称为Ridge回归(岭回归): 13、 LASSO回归: 使用L1正则的线性回归模型就称为LASSO回归: 14、Ridge回归与LASSO回归比较 ① L2-norm中,由于对各个维度的参数缩放在一个圆内缩放的,不可能导致有维度参数变为0的情况,那么也就不会产生稀疏解,实际应用中,数据的维度中是存在噪音和冗余的,稀疏的解可以找到有用的维度并且减少冗余, 提高回归预测的准确性和鲁棒性(减少了overfitting)(L1-norm可以达到最终解的稀疏性要求) ② Ridge模型具有较高的的准确性,鲁棒性以及稳定性,LASSO模型具有较高的求解速度 ③ 如果既要考虑稳定性又要考虑求解速度,就使用Elasitc Net 15、Elasitc Net算法: 同时使用L1和L2正则的线性回归模型就称为Elasitc Net算法(弹性网络算法): 16、模型效果判断: ① 误差平方和,越接近0表示模型越拟合训练数据 ② MSE的平方根,作用于MSE相同 ③ ④ TSS:总平方和TSS,表示样本之间的差异情况,是伪方差的m倍 ⑤ RSS:残差平方RSS,表示预测值与样本值之间的差异情况,是MSE的m倍 17、梯度下降 ① 目标函数求解: ② 初始化 ③ 沿着负梯度方向迭代,更新后的 ④ 记-机器学习(1)-回归算法 标签:fun 就是 连续 nbsp idt 梯度下降 线性 作用 最小二乘法 原文地址:https://www.cnblogs.com/leonchan/p/13560662.html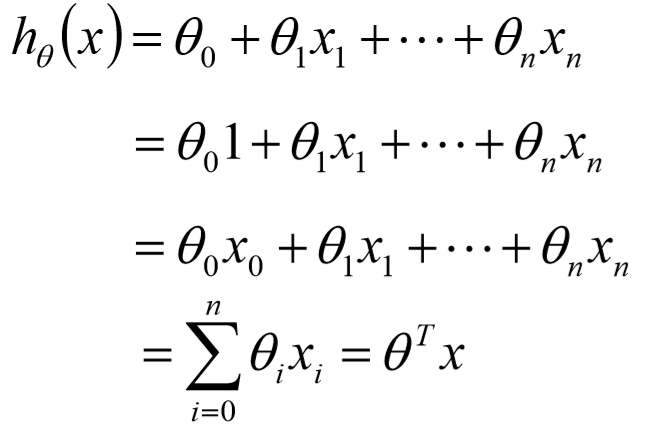
![]()
![]() 表示误差,是独立同分布的,服从均值为0,方差为某定值
表示误差,是独立同分布的,服从均值为0,方差为某定值![]() 的高斯分布(根据中心极限定理得出);但,实际问题中,很多随机现象可以看做众多因素的独立影响的综合反应,往往服从正态分布
的高斯分布(根据中心极限定理得出);但,实际问题中,很多随机现象可以看做众多因素的独立影响的综合反应,往往服从正态分布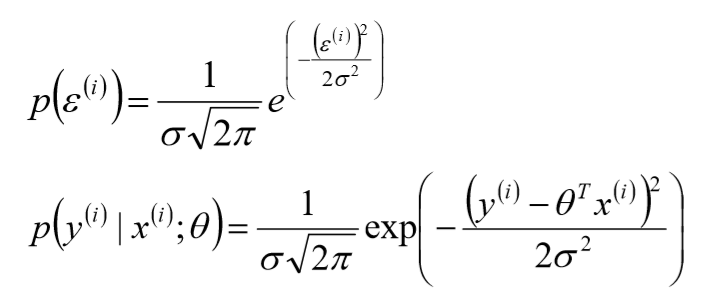
![]()
![]()
![]()
![]()
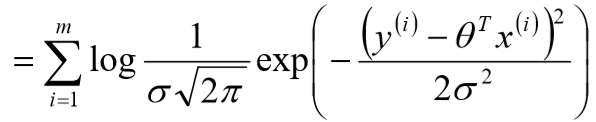
![]()
![]()
![]() ) 的求解过程:
) 的求解过程:![]()
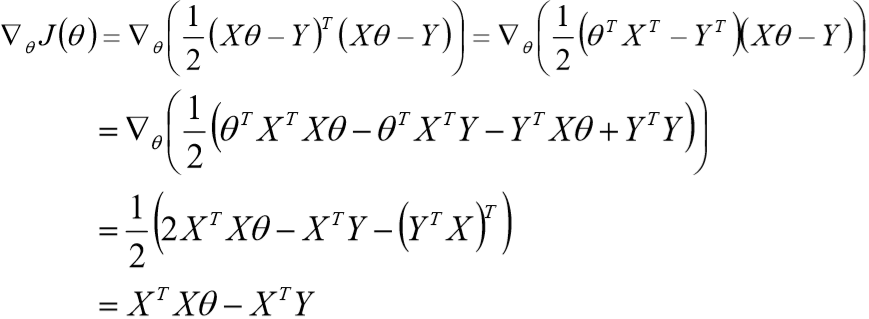
![]()
![]()
![]() 是可逆的;为了防止不可逆获取过拟合的问题存在,可以增加额外数据影响,导致最终的矩阵是可逆的:
是可逆的;为了防止不可逆获取过拟合的问题存在,可以增加额外数据影响,导致最终的矩阵是可逆的:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 值在样本空间中不能过大/过小,可以在目标函数之上增加一个平方和损失,
值在样本空间中不能过大/过小,可以在目标函数之上增加一个平方和损失,![]()
![]() ,这里这个正则项叫做L2-norm
,这里这个正则项叫做L2-norm![]()
![]()
![]()
![]()
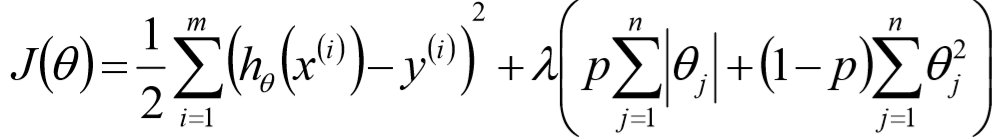
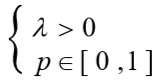
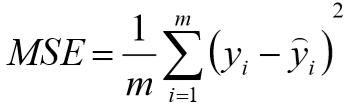
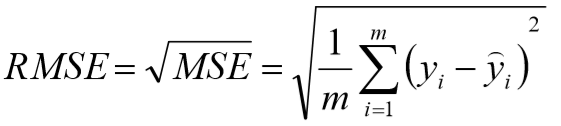
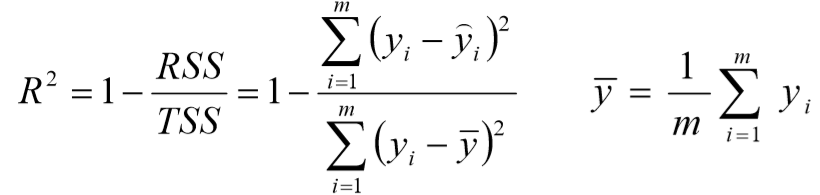
![]() 取值范围(负无穷,1],值越大表示模型越拟合训练数据;最优解是1,当模型预测为随机值的时候,有可能为负,若样本值恒为样本期望,
取值范围(负无穷,1],值越大表示模型越拟合训练数据;最优解是1,当模型预测为随机值的时候,有可能为负,若样本值恒为样本期望, ![]() 为0
为0![]()
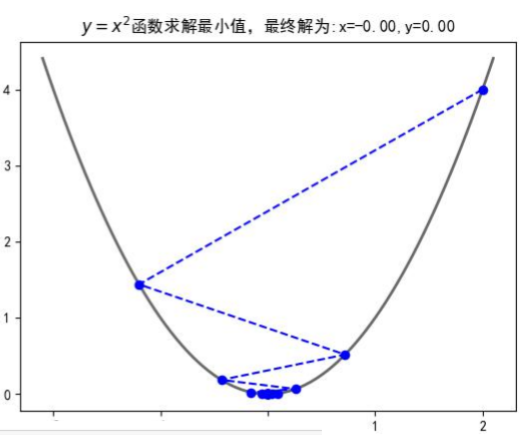
![]()
![]() (随机初始化,可以初始化为0)
(随机初始化,可以初始化为0)![]() 使得
使得![]() 更小
更小 ![]()
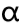 :学习率,步长
:学习率,步长