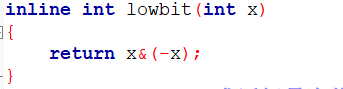树状数组
标签:图片 log pre 证明 include 单点 owb loading 增加
树状数组
对于区间之间的增删查改,如果单纯按照之前的想法就是O(1)查询,然后O(n)的时间复杂度去进行修改。
而树状数组查询和修改都是O(logn)的复杂度
接下来详细讲一下树状数组的基本操作
数组A(原数组) /// 数组C(树状数组)

原理: 找出每个数的二进制最低位的1,然后其他1归零,剩下的这个二进制数就是C数组元素的个数(也就是求lowbit)可以直接这么求(证明暂省)
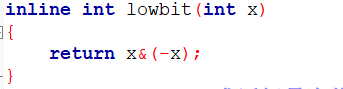

luoguP3374

#include
using namespace std;
const int maxn=5e5+7;
int a[maxn];
int c[maxn]={0};
inline int lowbit(int x)
{
return x&(-x);
}
int query(int x)///区间求和
{
int sum=0;
while (x>0)
{
sum+=c[x];
x=x-lowbit(x);
}
return sum;
}
void modify(int idx,int math,int k)///修改 k是边界 idx修改地址 math修改值,修改一个节点
{
while (idx
当然树状数组也支持区间修改和单点查询(一般采用差分数组和前缀和)
此时的C数组就是差分数组////B数组就是树状数组////A数组就是储存数组
luoguP3368

思维转化,区间修改的话不妨弄一个差分数组C,然后C[i]=A[i]-A[i-1]对于修改之后的值在区间[a,b]上增加一个d
只需要对于C[a]+d ///C[b+1]减去一个d即可实现区间修改操作

#include
using namespace std;
const int maxn=5e5+7;
int A[maxn]={0};///储存数组
int B[maxn]={0};///树状数组
int C[maxn]={0};///差分数组
inline int lowbit(int x)
{
return x&(-x);
}
int query(int x)///和上面的操作一样
{
int sum=0;
while (x>0)
{
sum+=B[x];
x=x-lowbit(x);
}
return sum;
}
void modify(int idx,int math,int k)
{
while (idx>n>>m;
int a,b,c,d;
for (int i=1;i>A[i];
C[i]=A[i]-A[i-1];
modify(i,C[i],n);///改动的地方只是把差分数组当作原来的原数组
}
while (m--)
{
cin>>a;
if (a==1)
{
cin>>b>>c>>d;
modify(b,d,n);///转化一下就是两点之间的修改操作
modify(c+1,-d,n);
}
else if (a==2)
{
cin>>b;
cout
一般讲来树状数组支持的就是单点查询、区间修改和区间求和、单点查改
其实严格意义上还可以进行树状数组维护区间最值(当然树套树我是不会的啦)//doge
树状数组
标签:图片 log pre 证明 include 单点 owb loading 增加
原文地址:https://www.cnblogs.com/qimang-311/p/13380293.html
文章来自:
搜素材网的
编程语言模块,转载请注明文章出处。
文章标题:
树状数组
文章链接:http://soscw.com/essay/72703.html
评论