重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十]
2021-04-14 03:27
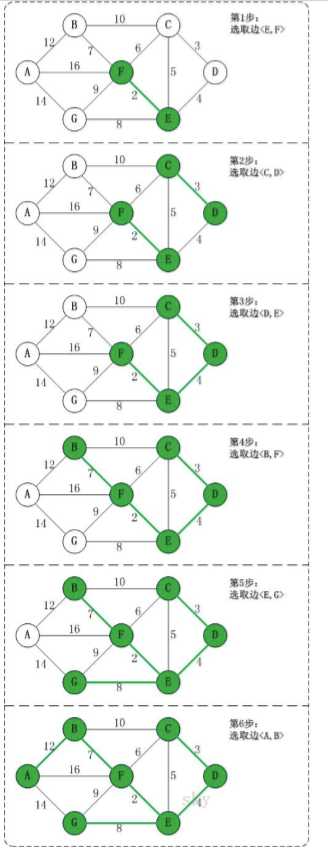
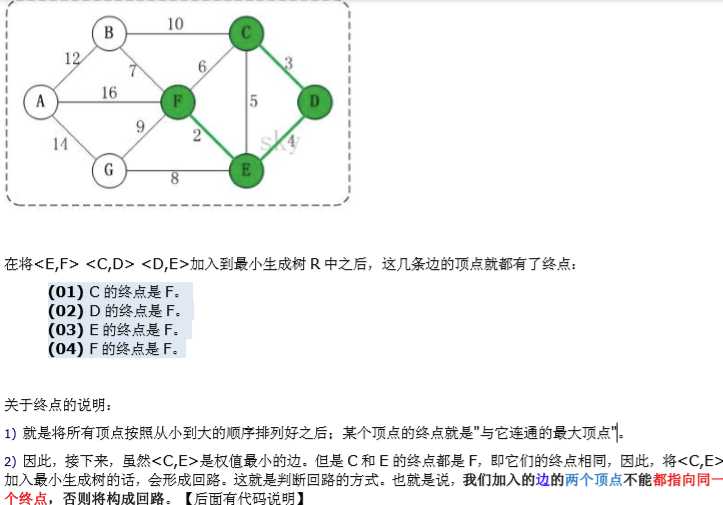
标签:int start 依据 line 技术 不用 mat lang var lan 这个和前面一节有关系,是这样子的,前面是用顶点作为参照条件,这个是用边作为参照条件。 图解如下: 每次选择最小的边。 但是会遇到一个小问题,就是会构成回路。 比如说第四步中,最小边是CE,但是没有选择CE,因为CE会形成回路。 那么如何判断是否有回路呢? 判断两个点的终点,是否一致。 这个是怎么来的呢?为什么判断终点是否一致就可以判断有回路呢? 是这样子的,如何两个点可以共同到达任何一个点,那么他们之间一定是通的,这一点是肯定的,如果他们本来就是通的,再在他们之间加一条那么肯定回路的。 那么为什么选择终点呢?是这样子的,假如他们之间选来不相通,他们肯定在两条路上。 假设选了cd和ef这两条路。那么他们这两条路的终点分别是d(c->d)和f(e->f),他们的终点不同,那么他们没有在一条路上,所以把c->d的终点d的终点设置为e->另一条路的终点也就是f,连接后所有节点都有公共的终点,那么终点就可以作为判断依据,这样就不用去遍历了。 代码如下: 结果: 重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十] 标签:int start 依据 line 技术 不用 mat lang var lan 原文地址:https://www.cnblogs.com/aoximin/p/13339377.html前言
正文
private static int INF = int.MaxValue;
static void Main(string[] args)
{
char[] vertexs = { ‘A‘, ‘B‘, ‘C‘, ‘D‘, ‘E‘, ‘F‘, ‘G‘ };
//克鲁斯卡尔算法的邻接矩阵
int[,] matrix = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF
},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
KruskaCase kruskaCase = new KruskaCase(vertexs,matrix);
kruskaCase.kruskal();
Console.ReadKey();
}
}
public class KruskaCase
{
private int edgeNum;//边的个数
private char[] vertexs;//顶点数组
private int[,] matrix;//邻接矩阵
private static int INF = int.MaxValue;
public KruskaCase(char[] vertexs, int[,] matrix)
{
int vlen = vertexs.Length;
//初始化顶点,避免污染数据
this.vertexs = new char[vlen];
for (int i=0;i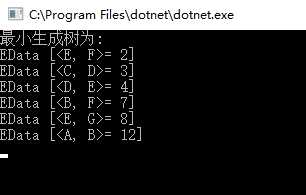
下一篇:在idea中打jar包的方式
文章标题:重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十]
文章链接:http://soscw.com/essay/75485.html