力扣_初级算法_其他_2~6题_和_数组_10~11题

标签：运算符   填充   tps   成长记   完全   lis   ima   思考   并且   

一位C++小白的力扣刷题_成长记录_欢迎 visit  ^_^

其他_第2题：汉明距离

题目描述：

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

举例：

示例:

输入: x = 1, y = 4

输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

解题思路：运用 位运算符 “>>” 。同时对 2 除余。（详见代码注释）

学习心得： 对于一些关于二进制的题，利用 位运算符 有时可以迎刃而解。

实现：（C++）

class Solution {
　　public:
　　　　int hammingDistance(int x, int y) {
　　　　int count=0;
　　　　while( x>0||y>0 )　　　　//只要 x和y 中海油一方大于零 继续比较他们的二进制位
　　　　 {
　　　　　　if( x%2!=y%2 ) 　　 // 举例：若 x 为奇数，x%2 后所得为 1
　　　　　　  count++;
　　　　　　x>>=1; 　　　　 //举例： 若 x=4 ，则 x 的二进制位可表示成 0100 ，x>>=1 相当于 x=x>>1, 答案为 x=010=2
　　　　　　y>>=1;
　　　　}
　　   return count;
　　}
};

运行结果： 

1
4

2

2

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

其他_第3题： 颠倒二进制位

题目描述：

 颠倒给定的 32 位无符号整数的二进制位。

举例：

示例 1：

输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：

输入：11111111111111111111111111111101
输出：10111111111111111111111111111111
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

解题思路：运用 按位于运算符“&”（也就是离散数学中的 “且” ，例如：1且0=0, 1且1=1， 0且0=0 ）。

学习心得：算法的思想重要啊。我是没想到这么做，看了力扣前辈的题解，深深佩服。

实现：（C++） 

class Solution {
public:
uint32_t reverseBits(uint32_t n) {
int i=32;
int res=0;
while( i-- ) //执行32次
{

res res+=n&1; // 举个栗子： res=0000， n=0101， 而 1=0001 ,则 n&1=0001， res+=n&1 的结果为 res=0001
n>>=1;
}
return res;
}
};

运行结果：

00000010100101000001111010011100

   964176192 (00111001011110000010100101000000)

   964176192 (00111001011110000010100101000000)

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

其他_第4题：帕斯卡三角形

题目描述：

举例：

示例:

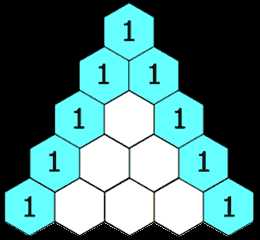
输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

解题思路：前两层单独考虑，第三层及其后面的层 循环输出。

学习心得：记得在大一上的 C语言编程题 中遇到过，这次又遇到了。我想用C++敲出来，无奈老师没教过

我们“C++ vector标准模板库”，只好搜索，自修“武功”。哈哈~

实现：（C++）

class Solution {
　　public:
　　　　vector> generate(int numRows) {
　　　　    vector> v( numRows ); 　　　　 //这里的 numRows 用来初始化 二维vector容器的 层数（即行数）
　　　　    int i,j;
　　　　    for( i=0;i 　　　　　　 {
　　　　　　　　v[i]=vector(i+1,0);　　　　 //给 容器里的所有元素 赋值0。 注：“i+1”是指 每层开辟的元素个数。
　　　　　　　　v[i][0]=1;　　　　　　　　　　//让 容器 的“左壁” 全为1
　　　　　　　　v[i][i]=1;　　　　　　　　　　 //让 容器 的“右壁” 全为1
　　　　　　}
　　　　　for( i=2;i 　　　　　　 for( j=1;j 　　　　　　　　v[i][j]=v[i-1][j-1]+v[i-1][j];
　　　　return v;
　　　　}
};

运行结果：

5

[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

其他_第5题：有效的括号

题目描述：

给定一个只包括 ‘(‘，‘)‘，‘{‘，‘}‘，‘[‘，‘]‘ 的字符串，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

举例：

示例 1:

输入: "()"
输出: true

示例 2:

输入: "()[]{}"
输出: true

示例 3:

输入: "(]"
输出: false

示例 4:

输入: "([)]"
输出: false

示例 5:

输入: "{[]}"
输出: true

解题思路：构造一个 栈（stack）。碰到 ‘ ( ‘ 或 ‘ [ ‘ 或 ‘ { ‘ 即入栈。 再碰到 ‘ ) ‘ 或 ‘ ] ‘ 或 ‘ } ‘ 就将栈顶的元素 拿出来 看看两者 是否是 一对儿。

学习心得：做这道题时，我深有感触，在这学期（大一下）我们做了离散数学实验一（利用真值表来求

主析取范式 和 主合取范式 ），其中就要用到这个“有效括号”的知识，但当时我不会 栈（stack）所以没

做出来（后来用的其他很怪的方法）。这道题让我对 栈（stack）的运用能力 又前进了一步~

实现：（C++）

class Solution {
　　public:
　　　　bool isValid(string s) {
　　　　int i;
　　　　int size=s.size();
　　　　stack sta;　　　　　　　　 //定义一个装 char类型数据的 栈sta（我自己这样缩写的）
　　　　for( i=0;i 　　　　  {
　　　　　　if( s[i]==‘(‘||s[i]==‘[‘||s[i]==‘{‘ ) 　　 //如果是这三个 符号 ，则放进 栈
　　　　　　    sta.push( s[i] );
　　　　　　else if( s[i]==‘)‘||s[i]==‘]‘||s[i]==‘}‘ )
　　　　　　  {
　　　　　　　　switch( s[i] )
　　　　　　　　  {
　　　　　　　　　　case ‘)‘: if( !sta.empty()&&sta.top()==‘(‘ )　　 //如果此时 栈不为空（这个别忘了，用来排除这种情况→案例为：")[]" ），并且 栈顶元素 与 s[i] 匹配，则弹出栈顶元素
　　　　　　　　　　　　　　   { sta.pop(); break; }
　　　　　　　　　　　　　　else
　　　　　　　　　　　　　　　return false;
　　　　　　　　　　case ‘]‘: if( !sta.empty()&&sta.top()==‘[‘ )
　　　　　　　　　　　　　　   { sta.pop(); break; }
　　　　　　　　　　　　　　else
  　　　　　　　　　　　　　　 return false;
　　　　　　　　　　case ‘}‘: if( !sta.empty()&&sta.top()==‘{‘ )
　　　　　　　　　　　　　　  { sta.pop(); break; }
　　　　　　　　　　　　　　else
　　　　　　　　　　　　　　   return false;
　　　　　　　　　　　　　　default: return false;　　　　 //如果字符串里面参加其他 不符合要求的符号，例如“ 　　　　　　　　　　}

　　　　　　　　}
　　　　}
　　return sta.empty(); 　　　　　　 //最后，当 栈为空时 ，返回 1（即true），反之则返回 false
　　}
};

（其中一个）运行结果：

"()"

true

true

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

 其他_第6题：缺失数字

 题目描述：

给定一个包含 0, 1, 2, ..., n 中 n 个数的序列，找出 0 .. n 中没有出现在序列中的那个数。

举例：

示例 1:

输入: [3,0,1]
输出: 2

示例 2:

输入: [9,6,4,2,3,5,7,0,1]
输出: 8

解题思路：这道题，要灵活运用 按位异或运算符 “ ^ ” ，真的。并要知道 “ ^ ” 具有结合律和交换律。 举例：0^0=1, 0^1=1,1^1=0, 3^4^3=3^(4^3)=3^(3^4)=3^3^4=0^4=4

学习心得：今天，感觉最大的收获之一，就是学到了 异或“^”这玩意，嘿，小家伙，竟然满足 结合律和交换律

（当然后面也查了 还满足 分配律）。然后，它这一性质就很适合解 这道题。

实现：（C++）

class Solution {
　　public:
　　　　int missingNumber(vector& nums) {
　　　　int res=nums.size(); 　　　　　　 //这句话是个关键。因为 “vector容器”里 肯定有个最大值 ，即是nums.size()
　　　　  for( int i=0;i 　　　　　{
　　　　　　res^=nums[i]; 　　　　　　 //举个例子： nums里面装的有 “0,2,4,1” ，而res一来即是 4
　　　　　　res^=i; 　　　　　　 　　   //（接上一注释） 则执行完全部for循环时： res = 4 ^ 0 ^ 0 ^ 2^ 1 ^ 4 ^ 2 ^ 1 ^ 3 = 3（利用 异或运算符的交换律和结合律解出，详见 上面的 解题思路）
　　　　　}
　　　　return res;
　　}
};

运行结果：

[3,0,1]

2

2

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

数组_第10题：有效的数独

题目描述：

判断一个 9x9 的数独是否有效。只需要根据以下规则，验证已经填入的数字是否有效即可。

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

上图是一个部分填充的有效的数独。

数独部分空格内已填入了数字，空白格用 ‘.‘ 表示。

举例：

示例 1:

输入:
[
  ["5","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: true

示例 2:

输入:
[
  ["8","3",".",".","7",".",".",".","."],
  ["6",".",".","1","9","5",".",".","."],
  [".","9","8",".",".",".",".","6","."],
  ["8",".",".",".","6",".",".",".","3"],
  ["4",".",".","8",".","3",".",".","1"],
  ["7",".",".",".","2",".",".",".","6"],
  [".","6",".",".",".",".","2","8","."],
  [".",".",".","4","1","9",".",".","5"],
  [".",".",".",".","8",".",".","7","9"]
]
输出: false
解释: 除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。
     但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

说明:

• 一个有效的数独（部分已被填充）不一定是可解的。
• 只需要根据以上规则，验证已经填入的数字是否有效即可。
• 给定数独序列只包含数字 1-9 和字符 ‘.‘ 。
• 给定数独永远是 9x9 形式的。

 解题思路：分三种情况来判断，①从 行 的角度来看。 ②从 列 的角度来看。 ③从 格 的角度来看。 根据三种情况，分别建立三个 哈希表。（详见代码里的注释）

学习心得：通过做这道题，我对 hash table（哈希表）又有了更进一步地认识。

实现：（C++）

class Solution {
　　public:
　　　　bool isValidSudoku(vector>& board) {
　　　　int row_judge[9][9]={0}; 　　　　 //初始化用来检索 每行是否合格的 “行”-哈希表
　　　　int col_judge[9][9]={0}; 　　　　 //初始化用来检索 每列是否合格的 “列”-哈希表
　　　　int block_judge[9][9]={0};　　　　 //初始化用来检索 每个小九宫格是否合格的 “格”-哈希表
　　　　int i,j;
　　　　for( i=0;i 　　　　  for( j=0;j 　　　　　{
　　　　　　if( board[i][j]==‘.‘ ) continue; 　　　　　　　 // 检索到 ‘ . ‘ 直接continue
　　　　　　int flag=board[i][j]-‘0‘; 　　　　　　　　　　 //注意：数组的下标是 int类型 ，而board[i][j]是char类型
　　　　　　row_judge[i][ flag-1 ]+=1; 　　　　　　　　 //将在 i 行出现的 下标为 flag-1 的 “行”-哈希表 的对应位置 加上1
　　　　　　col_judge[ flag-1 ][j]+=1; 　　　　　　　　 //为什么flag要减1？ 因为 要转成数组下标
　　　　　　block_judge[ i/3*3+j/3 ][ flag-1 ]+=1;　　　　 //这句挺关键的。“ i/3*3+j/3 ” 的意思是 从左到右、从上到下 的九宫格的 编号数
　　　　　　　　　　　　　　　　　　　　　　　　　　//举个栗子： i=1,j=3时， i/3*3+j/3=1 ,表示 编号为1 的九宫格。 而当i=j=0， 则编号为0
　　　　　　　　　　　　　　　　　　　　　　　　　　//这里把 九宫格 理顺了，理成了 从 “行” 看的角度， 你细品
　　　　　　if( row_judge[i][ flag-1 ]==2 ) return false;
　　　　　　if( col_judge[ flag-1 ][j]==2 ) return false; 　　 //如果 “列”-哈希表 的对应位置的元素值为2， 说明 col_judge[ flag-1 ][j] 加了两次，进而说明 该列有相同的元素，不符合要求，返回 false
　　　　　　if( block_judge[ i/3*3+j/3 ][ flag-1 ]==2 ) return false;
　　　　　}
　　return true;
　　}
};

运行结果：

[["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]

true

true

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

 数组_第11题：旋转图像

题目描述：

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

举例：

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

解题思路：先转置，再左右镜像翻转。（图来源于 力扣）

学习心得：原来翻转都有这么大的学问。我后面思考了一下，感觉 矩阵的转置 就好像是让矩阵“照镜子”，

然后若再来个镜像翻转，该镜子里矩阵又从 镜子 里回来了。

实现：（C++）

class Solution {
　　public:
　　　　void rotate(vector>& matrix) {
　　　　int i,j;
　　　　int row_size=matrix.size(); 　　　　　　 //这里求的是 变量名叫matrix的“vector容器”的 行的数量，不是求 容器内部的元素个数哈
　　　　for( i=0;i 　　　　    for( j=0;j 　　　　　　swap( matrix[i][j],matrix[j][i] );　　　　 //交换
　　　　for( i=0;i 　　　　   reverse( matrix[i].begin(),matrix[i].end() );　　 //①新学到一个函数reverse( 某个对于元素的指向，另一个对于某个元素的指向 )，括号里的内容可能表达的不准确，欢迎评论，帮我提出纠正。                                                                                                //reverse()函数 位于 C++的List标准模板库
　　　　}
};

运行结果：

[[1,2,3],[4,5,6],[7,8,9]]

[[7,4,1],[8,5,2],[9,6,3]]

[[7,4,1],[8,5,2],[9,6,3]]

力扣_初级算法_其他_2~6题_和_数组_10~11题

标签：运算符   填充   tps   成长记   完全   lis   ima   思考   并且   

原文地址：https://www.cnblogs.com/Wang-dou-dou/p/13296724.html