排序算法全（Java）

2021-04-18 04:30

阅读：869

标签：static pre 分组 quic loading item tostring 一般来说空间

排序算法

技术图片

冒泡排序（Bubble Sort）--稳定实质：把小（大）的元素往前（后）调

步骤一：比较相邻的元素。如果第一个比第二个大，就交换他们两个。

步骤二：对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

步骤三：针对所有的元素重复以上的步骤，除了最后一个。

步骤四：持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

package org.hrose.sort;

import java.util.Arrays;

public class BuddleSort {
    public static void main(String[] args) {
int  [] array = {54,8,5,45,5,95,15};
BuddleSort(array);
    }
    public static void BuddleSort(int [] array){
        boolean flag =false;
        for(int i =0;i){
            for(int j =0;j1-i;j++){
                if(array[j+1]array[j]){
                    flag=true;
                    int temp = array[j+1];
                    array[j+1] = array[j];
                    array[j] = temp;
                }

            }if(!flag){
                break;
            }else{
                flag=false;
            }//
        }
        System.out.println(Arrays.toString(array));
    }
}

选择排序（Selection Sort）--不稳定

步骤一：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置

步骤二：再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

步骤。。。：以此类推，直到所有元素均排序完毕。

package org.hrose.sort;

import java.util.Arrays;

public class SelectSort {
    public static void main(String[] args) {
int [] array ={45,8,8,8,84,846,4,94};
SelectSort(array);
    }

    public static void SelectSort(int[] array) {
        for (int j =0;j1;j++) {
            int minIndex = j;
            int min = array[j];
            for (int i=j+1; i ) {
                if (min > array[i]) {
                    min = array[i];
                    minIndex = i;
                }
            }
            if(minIndex!=0){
                array[minIndex] = array[j];
                array[j]=min;

            }
        }
        System.out.println(Arrays.toString(array));
    }
}

插入排序（Insertion Sort）--稳定适用于已经有部分数据已经排好，并且排好的部分越大越好。一般在输入规模大于1000的场合下不建议使用插入排序

基本思想：

插入排序的工作方式像许多人排序一手扑克牌。开始时，我们的左手为空并且桌子上的牌面向下。然后，我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置，我们从右到左将它与已在手中的每张牌进行比较。拿在左手上的牌总是排序好的，原来这些牌是桌子上牌堆中顶部的牌。

最优 On

插入排序是指在待排序的元素中，假设前面n-1(其中n>=2)个数已经是排好顺序的，现将第n个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。

package org.hrose.sort;

import java.util.Arrays;

public class InsertSort {
    public static void main(String[] args) {
        int[] array = {78, 88, 68, 2, 5, 3};
        insertSort(array);
    }

    public static void insertSort(int[] array) {
        for (int i =1;i) {
            int insertValue = array[i];
            int initIndex=i-1;
            while (initIndex>=0&&insertValuearray[initIndex]){
                array[initIndex+1]=array[initIndex];
                initIndex--;
            }
            array[initIndex+1]=insertValue;
        }
        System.out.println(Arrays.toString(array));
    }
}

希尔排序(Shell‘s Sort) --不稳定是直接插入排序算法的一种更高效的改进版本

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

不稳定原因：

由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。

排序过程：

步骤一：先取一个正整数d1

步骤二：然后取d2

步骤。。。：直至di=1，即所有记录放进一个组中排序为止。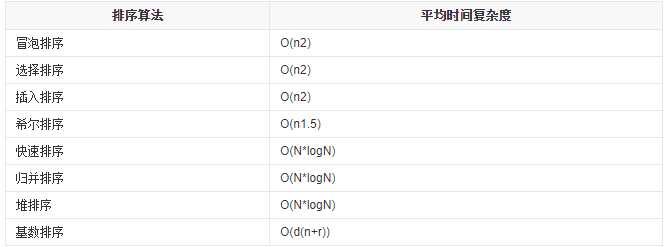

package org.hrose.sort;

import java.util.Arrays;

public class ShellSort {
    public static void main(String[] args) {
      int [] array ={515,78,8,84,96,49,49,8,498};
      ShellSort2(array);
    }

    public static void ShellSort2(int [] array){
        for(int gap = array.length/2;gap>0;gap /=2){
            for(int i = gap;i){
                int j =i;
                int temp = array[j];
                if(array[j]gap]){
                       while(j-gap>=0&&array[j]gap]){
                           array[j] = array[j-gap];
                           j -= gap;
                       }
                       array[j] = temp;
                }
            }
        }
        System.out.println(Arrays.toString(array));
    }

快速排序（Quicksort）冒泡的改进呃。。。

快速排序算法通过多次比较和交换来实现排序，其排序流程如下：

步骤一：首先设定一个分界值，通过该分界值将数组分成左右两部分。

步骤二：将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。

步骤三：然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。

步骤四：重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

package org.hrose.sort;

import java.util.Arrays;

public class QuickSort {
    public static void main(String[] args) {
        int[] array = {15, 33, 18, 47, 66, 28,18,93,24};
        QuickSort(array, 0, array.length - 1);
        System.out.println("array" + Arrays.toString(array));
    }
    public static void QuickSort(int [] array , int left, int right){
        int l =left;
        int r = right;
        int povit = array[(l+r)/2];
        while(lr){
            while(array[l]povit){
                l+=1;
            }
            while(array[r]>povit){
                r-=1;
            }
            if(l>=r){
                break;
            }
            int temp = array[l];
            array[l] = array[r];
            array[r] = temp;
            if(array[l] ==povit){
                r-=1;
            }
            if(array[r]==povit){
                l+=1;
            }
        }
        if(l==r){
            l+=1;
            r-=1;
        }
        if(right>l){
            QuickSort(array,l,right);
        }
        if(leftr){
            QuickSort(array,left,r);
        }
    }
}

归并排序*（Merge Sort）--稳定

该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并操作的工作原理如下：

步骤一：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

步骤二：设定两个指针，最初位置分别为两个已经排序序列的起始位置

步骤三：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

步骤。。。：重复步骤三直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾

package org.hrose.sort;

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) {

        int [] array={41,8,4,89,48,8,84,8,6,6,8,48,45,8,4};
        int [] temp = new int [array.length];
        mergeSort(array,0,array.length-1,temp);
        System.out.println(Arrays.toString(array));
    }
    public static void mergeSort(int [] arry,int left,int right,int []temp){
     if(leftright){
 int mid=(left+right)/2;
      mergeSort(arry,left,mid,temp);
    mergeSort(arry,mid+1,right,temp);
         merge(arry,left,mid,right,temp);
     }

    }  public static void merge(int [] arry,int left,int mid,int right,int []temp){
        int i =left;
        int j =mid+1;
        int t =0;

        while(iright){
          if(arry[i]arry[j]){
              temp[t]=arry[i];
              t+=1;
              i+=1;

          }else {
              temp[t] = arry[j];
                  j+=1;
                  t+=1;
          }
        }
while(imid){
    temp[t]=arry[i];
    t+=1;
    i+=1;
}
while(jright){
    temp[t] = arry[j];
    j+=1;
    t+=1;
}
  t=0;
 int templeft =left;
while(templeftright){
 arry[templeft] = temp[t];
  t+=1;
templeft+=1;
}

  }
}

堆排序（Heapsort）

利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆的操作

最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
创建最大堆（Build Max Heap）：将堆中的所有数据重新排序
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算

package org.hrose.sort;

import java.util.Arrays;

/**
 * 代码来源于网络
 */
public class HeapSort {
    public static void main(String[] args) {
        int [] array={41,8,4,89,48,8,84,8,6,6,8,48,45,8,4};
        int[] a = heapSort(array);
        System.out.println(Arrays.toString(a));

    }
    public static int[] heapSort(int[] array) {
        //这里元素的索引是从0开始的,所以最后一个非叶子结点array.length/2 - 1
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            adjustHeap(array, i, array.length);  //调整堆
        }

        // 上述逻辑，建堆结束
        // 下面，开始排序逻辑
        for (int j = array.length - 1; j > 0; j--) {
            // 元素交换,作用是去掉大顶堆
            // 把大顶堆的根元素，放到数组的最后；换句话说，就是每一次的堆调整之后，都会有一个元素到达自己的最终位置
            swap(array, 0, j);
            // 元素交换之后，毫无疑问，最后一个元素无需再考虑排序问题了。
            // 接下来我们需要排序的，就是已经去掉了部分元素的堆了，这也是为什么此方法放在循环里的原因
            // 而这里，实质上是自上而下，自左向右进行调整的
            adjustHeap(array, 0, j);
        }
        return array;
    }

    /**
     * 整个堆排序最关键的地方
     * @param array 待组堆
     * @param i 起始结点
     * @param length 堆的长度
     */
    public static void adjustHeap(int[] array, int i, int length) {
        // 先把当前元素取出来，因为当前元素可能要一直移动
        int temp = array[i];
        for (int k = 2 * i + 1; k //2*i+1为左子树i的左子树(因为i是从0开始的),2*k+1为k的左子树
            // 让k先指向子节点中最大的节点
            if (k + 1 //如果有右子树,并且右子树大于左子树
                k++;
            }
            //如果发现结点(左右子结点)大于根结点，则进行值的交换
            if (array[k] > temp) {
                swap(array, i, k);
                // 如果子节点更换了，那么，以子节点为根的子树会受到影响,所以，循环对子节点所在的树继续进行判断
                i  =  k;
            } else {  //不用交换，直接终止循环
                break;
            }
        }
    }

    /**
     * 交换元素
     * @param arr
     * @param a 元素的下标
     * @param b 元素的下标
     */
    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

基数排序（radix sort） --稳定

原理：

将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

基数排序的方式可以采用LSD（最低位优先）或MSD（最高位优先），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

package org.hrose.sort;

import java.util.Arrays;

public class RadixSort {
    public static void main(String[] args) {
int [] array = {50,5,8,4,9,2,8,7,66,88,44,93};
radixSort(array);
    }


    public static void radixSort(int[] array) {
        int max = array[0];
        for (int i = 0; i ) {
            if (max  array[i]) {
                max = array[i];

            }
        }
        int maxLength = (max + "").length();

            int[][] bucket = new int[10][array.length];
            int[] bucketElementCount = new int[10];
        for (int i =0,n=1;i ) {
            for (int j = 0; j ) {
                int digitOfElement = array[j] / n % 10;
                bucket[digitOfElement][bucketElementCount[digitOfElement]] = array[j];
                bucketElementCount[digitOfElement]++;
            }
            int index = 0;
            for (int k = 0; k ) {
                if (bucketElementCount[k] != 0) {
                    for (int l = 0; l ) {
                        array[index++] = bucket[k][l];
                    }
                }
                bucketElementCount[k]=0;
            }
            System.out.println(Arrays.toString(array));

        }
    }
}

排序算法全（Java）

标签：static pre 分组 quic loading item tostring 一般来说空间

原文地址：https://www.cnblogs.com/smallores/p/smalloresforsort.html

上一篇：快速突击 Spring Cloud Gateway

下一篇：SpringBoot整合minio快速入门

文章来自：搜素材网的编程语言模块，转载请注明文章出处。
文章标题：排序算法全（Java）
文章链接：http://soscw.com/essay/76186.html

亲，登录后才可以留言！

排序算法全（Java）

评论

热门文章

推荐文章

最新文章

置顶文章