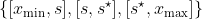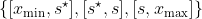R语言中自编基尼系数的CART回归决策树的实现
2021-04-21 21:30
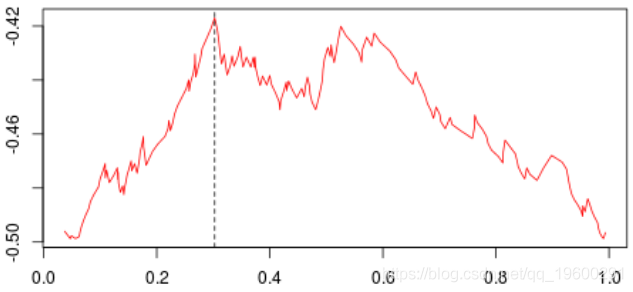
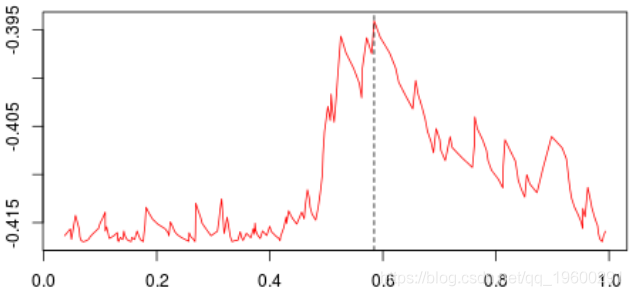
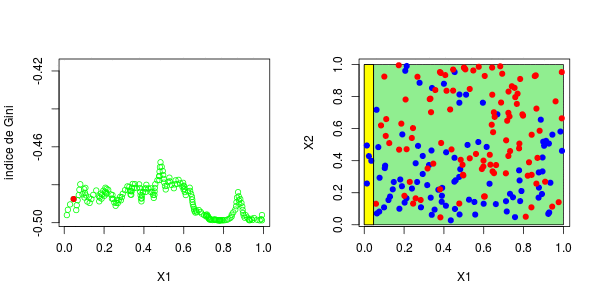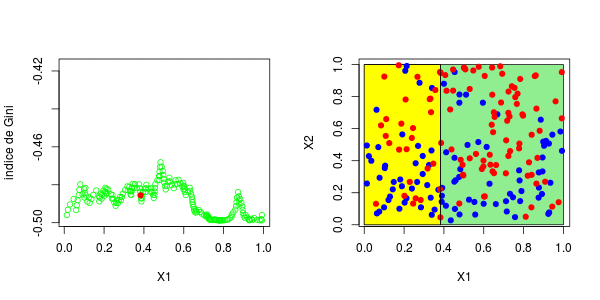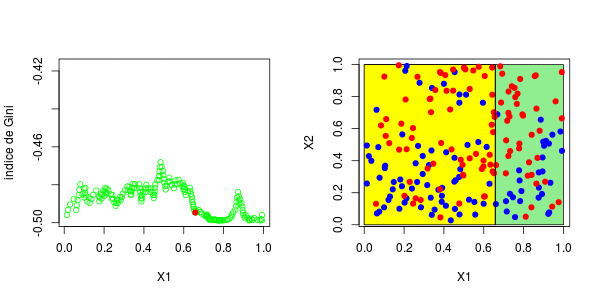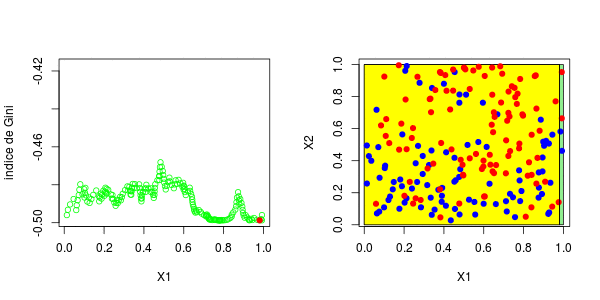
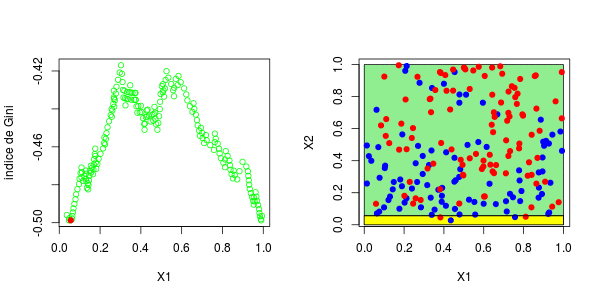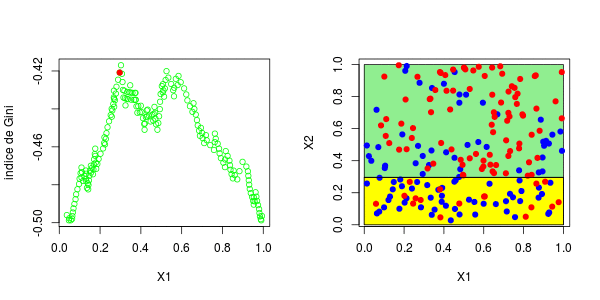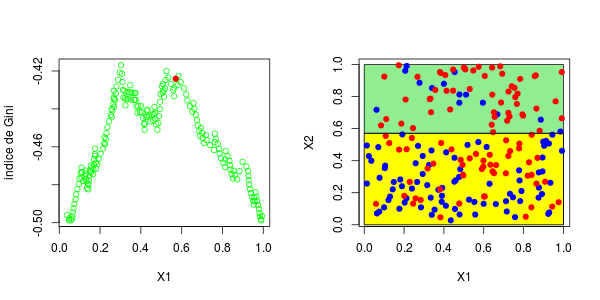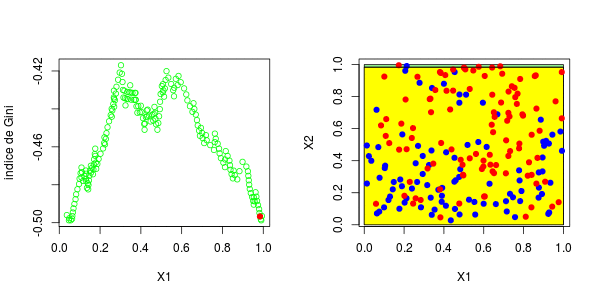
标签:spl 网站 序列 water tail 预测 gre segment 分割 具有一个因变量(感兴趣的变量)和两个连续的自变量( 变量 理论分区如下 在这里,可以将样本绘制在下方(请注意,第一个变量在上方的y轴上,在下方的x轴上),蓝色点 等于1,红色点等于0, 为了构造树,我们需要一个分区critera。最标准的可能是Gini的索引,当将s分为两类时,可以写出该索引, 在此表示 或 将分为三类时,表示为 等等,这里 在传统上,当我们考虑两个等级时,或者在三个等级的情况下。 同样,这里的想法是使距离最大化:想法是区分,所以我们希望样本尽可能不独立。要计算基尼系数 我们只需构造列联表,然后计算上面给出的数量。首先,假设只有一个解释变量。我们将样本一分为二,并使用所有可能的分割值 然后,我们为所有这些值计算基尼系数。结是使基尼系数最大化的值。有了第一个节点后,我们将继续保留(从现在开始将其称为 或这个 也就是说,我们在上一个结的下方或上方分割。然后我们进行迭代。代码可以是这样的, 第一步,基尼系数的值如下: 最高约为0.3。然后,我们尝试分三部分构造一个分区(拆分为0.3以下或以上)。我们得到以下基尼系数图(作为第二个节点的函数) 当样本在0.6左右分裂(这成为我们的第二个节点)时最大。等,现在,让我们将代码与标准R函数进行比较, 我们确实获得了类似的结:第一个为0.302,第二个为0.584。因此,构造树并不难... 现在,如果我们考虑两个解释变量,该怎么办?保持不变,除了分区的编写现在变得更加复杂。为了找到第一个节点,我们考虑了两个分量的所有值,然后再次保持最大化基尼指数的值, 这些图如下所示并获得了右侧的分区, 或者我们分割第二个分区(然后得到以下分区), 在这里,最好先分割第二个变量。实际上,我们回到了前面讨论的一维情况:正如预期的那样,最好在0.3左右进行分割。以下代码已确认这一点, 对于第二个结,应考虑四种情况:在第二个变量上再次分裂(再次),在上一个结之上或之下(请参见左下方)或在第一个变量上分裂。然后在上一个结的下方或上方设置一个分区(请参见右下方), 为了使树可视化,代码如下 注意,我们也可以可视化该分区。 参考文献 1.从决策树模型看员工为什么离职 2.R语言基于树的方法:决策树,随机森林,套袋Bagging,增强树数据分析 3.python中使用scikit-learn和pandas决策树进行鸢尾花数据分类 4.R语言对用电负荷时间序列数据进行K-medoids聚类建模和GAM回归 5.R语言k-Shape算法股票价格时间序列聚类 6.r语言鸢尾花iris数据集的层次聚类 7.Python Monte Carlo K-Means聚类实战研究 8.用R进行网站评论文本挖掘聚类 9.Python中的Apriori关联算法市场购物篮分析 10.通过Python中的Apriori算法进行关联规则挖掘 11.使用LSTM神经网络预测爱尔兰的电力消耗 12.用R语言实现神经网络预测股票实例 R语言中自编基尼系数的CART回归决策树的实现 标签:spl 网站 序列 water tail 预测 gre segment 分割 原文地址:https://www.cnblogs.com/tecdat/p/13279014.html
原文链接
http://tecdat.cn/?p=14056
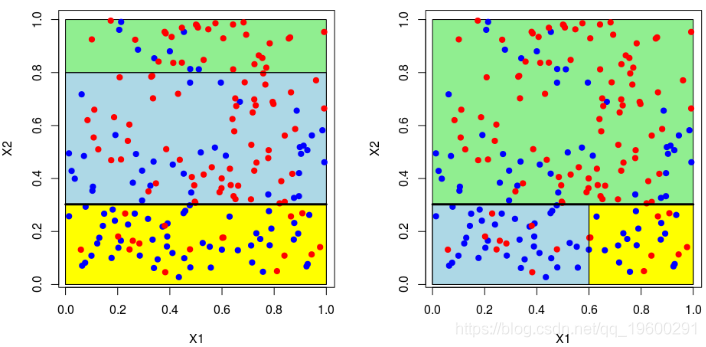
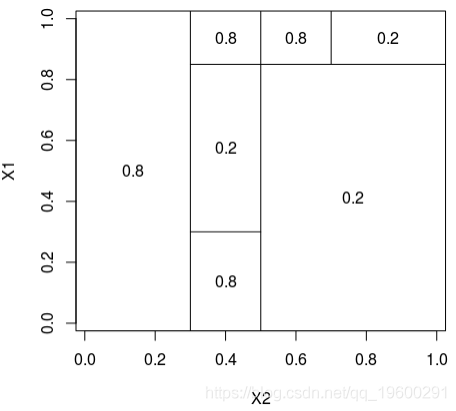
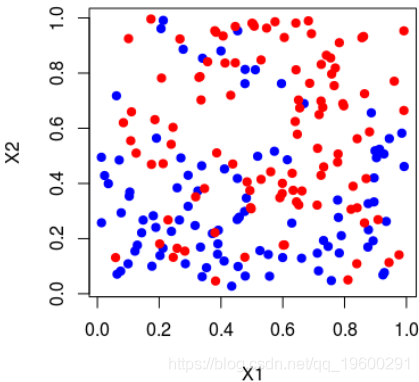
本文为了说明回归树的构造(使用CART方法),考虑以下模拟数据集,
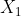 和
和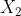 )。
)。
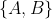
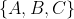
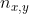 只是属于分区的观测值的计数,
只是属于分区的观测值的计数, 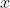 其 取值为
其 取值为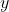 。但是可以考虑其他标准,例如卡方距离,
。但是可以考虑其他标准,例如卡方距离,  ,即
,即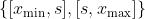
 )。我们通过寻找最佳第二选择来重申:给定一个根节点,考虑将样本一分为三的值,并给出最高的基尼系数,因此,我们考虑以下分区
)。我们通过寻找最佳第二选择来重申:给定一个根节点,考虑将样本一分为三的值,并给出最高的基尼系数,因此,我们考虑以下分区