重新整理数据结构与算法(c#)—— 树的节点删除[十八]
2021-04-25 22:30
标签:etl http 需要 over 子节点 setname string null image 你好这里的一个删除,指的是如果删除的叶子节点则直接删除,如果删除的是非叶子节点,则删除的是这颗子树。 这样删除的场景并不多,这种删除方式了解即可。 十七和十六没有放树图,把树图放一下。 节点模型: 树模型: 测试: 结果: 重新整理数据结构与算法(c#)—— 树的节点删除[十八] 标签:etl http 需要 over 子节点 setname string null image 原文地址:https://www.cnblogs.com/aoximin/p/13253019.html前言
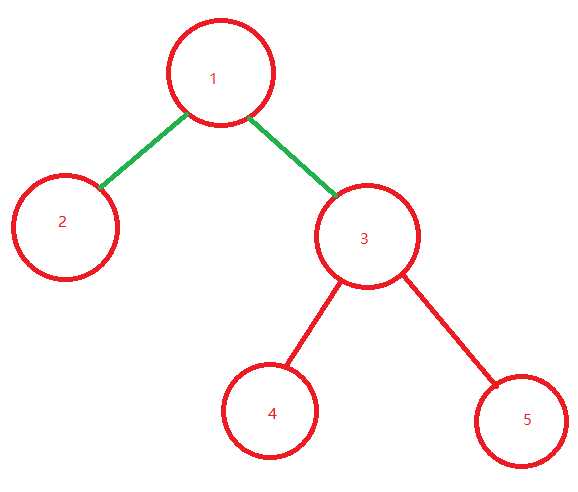
正文
public class HeroNode
{
private int no;
private string name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, string name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no)
{
this.no = no;
}
public String getName()
{
return name;
}
public void setName(String name)
{
this.name = name;
}
public HeroNode getLeft()
{
return left;
}
public void setLeft(HeroNode left)
{
this.left = left;
}
public HeroNode getRight()
{
return right;
}
public void setRight(HeroNode right)
{
this.right = right;
}
public override string ToString()
{
return "姓名:" + name + "编号:" + no;
}
//编写前序遍历的方法 是根、左、右
public void preOrder() {
Console.WriteLine(this);
if (this.left != null)
{
this.left.preOrder();
}
if (this.right != null)
{
this.right.preOrder();
}
}
//中序遍历 是左、根、右
public void infixOrder() {
if (this.left != null)
{
this.left.infixOrder();
}
Console.WriteLine(this);
if (this.right != null)
{
this.right.infixOrder();
}
}
// 后续遍历为 左、右、根
public void postOrder()
{
if (this.left != null)
{
this.left.postOrder();
}
if (this.right != null)
{
this.right.postOrder();
}
Console.WriteLine(this);
}
//前序遍历查找
public HeroNode preOrderSearch(int no)
{
HeroNode resNode = null;
record();
if (this.no == no)
{
return this;
}
if (this.left != null)
{
resNode=this.left.preOrderSearch(no);
}
if (resNode != null)
{
return resNode;
}
if (this.right != null)
{
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public HeroNode infixOrderSearch(int no)
{
HeroNode resNode = null;
if (this.left != null)
{
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null)
{
return resNode;
}
record();
if (this.no == no)
{
return this;
}
if (this.right != null)
{
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历查找
public HeroNode postOrderSearch(int no)
{
HeroNode resNode = null;
if (this.left != null)
{
resNode = this.left.postOrderSearch(no);
}
if (resNode != null)
{
return resNode;
}
if (this.right != null)
{
resNode = this.right.postOrderSearch(no);
}
if (resNode != null)
{
return resNode;
}
record();
if (this.no == no)
{
resNode=this;
}
return resNode;
}
public void delNode(int no)
{
if (this.left!=null&&this.left.no==no)
{
this.left = null;
}
if (this.right != null && this.right.no == no)
{
this.right = null;
}
if (this.left != null)
{
this.left.delNode(no);
}
if (this.right != null)
{
this.right.delNode(no);
}
}
public void record()
{
Console.WriteLine("查找步骤为:名字" + this.name + " 编号:" + this.no);
}
}
public class BinaryTree
{
private HeroNode root;
public void setRoot(HeroNode root)
{
this.root = root;
}
//前序遍历
public void preOrder()
{
if (this.root != null)
{
this.root.preOrder();
}
else
{
Console.WriteLine("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder()
{
if (this.root != null)
{
this.root.infixOrder();
}
else
{
Console.WriteLine("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder()
{
if (this.root != null)
{
this.root.postOrder();
}
else
{
Console.WriteLine("二叉树为空,无法遍历");
}
}
//前序遍历查找
public HeroNode preOrderSearch(int no)
{
if (root != null)
{
return this.root.preOrderSearch(no);
} else {
return null;
}
}
//中序遍历查找
public HeroNode infixOrderSearch(int no)
{
if (root != null)
{
return this.root.infixOrderSearch(no);
}else
{
return null;
}
}
//后序遍历查找
public HeroNode postOrderSearch(int no)
{
if (root != null)
{
return this.root.postOrderSearch(no);
}else {
return null;
}
}
public void delNode(int no)
{
if (root != null)
{
if (root.getNo() == no)
{
root = null;
return;
}
root.delNode(no);
}
}
}
static void Main(string[] args)
{
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
//设置节点
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
//删除4
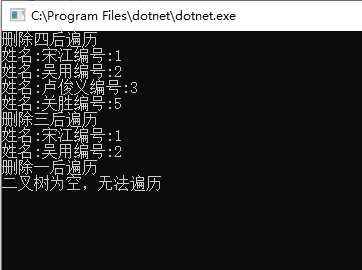
Console.WriteLine("删除四后遍历");
binaryTree.delNode(4);
binaryTree.preOrder();
//删除3
Console.WriteLine("删除三后遍历");
binaryTree.delNode(3);
binaryTree.preOrder();
//删除1
Console.WriteLine("删除一后遍历");
binaryTree.delNode(1);
binaryTree.preOrder();
Console.ReadKey();
}
文章标题:重新整理数据结构与算法(c#)—— 树的节点删除[十八]
文章链接:http://soscw.com/essay/79556.html