leetcode题解之33. 搜索旋转排序数组
2021-05-04 13:29
阅读：737
?? 视频题解
刷新重试诊断
code：
vid:
uuid:
requestId:
播放时间：
提示信息
字幕
倍速
清晰度
音轨
倍速正常
字幕Off
音轨
清晰度
00:00 / 05:38
确认取消
?? 文字题解
方法一：二分搜索
思路和算法
题目要求算法时间复杂度必须是 的级别，这提示我们可以使用二分搜索的方法。
但是数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分搜索吗？答案是可以的。
可以发现的是，我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。
这启示我们可以在常规二分搜索的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分搜索的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分：
- 如果
[l, mid - 1]是有序数组，且target的大小满足 ，则我们应该将搜索范围缩小至[l, mid - 1]，否则在[mid + 1, r]中寻找。 - 如果
[mid, r]是有序数组，且target的大小满足 ，则我们应该将搜索范围缩小至[mid + 1, r]，否则在[l, mid - 1]中寻找。
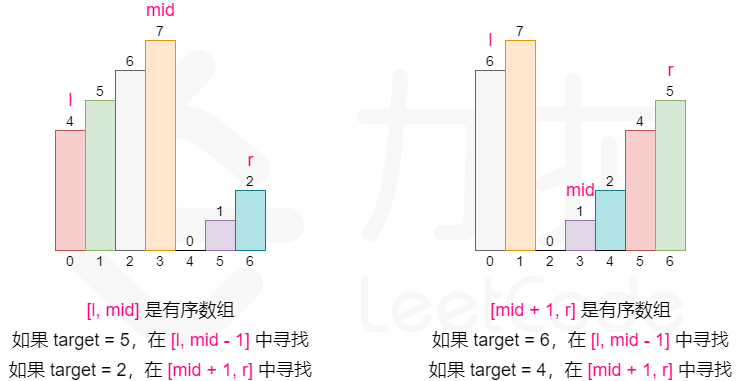
需要注意的是，二分的写法有很多种，所以在判断 target 大小与有序部分的关系的时候可能会出现细节上的差别。
class Solution {
public:
int search(vectorint>& nums, int target) {
int n = (int)nums.size();
if (!n) return -1;
if (n == 1) return nums[0] == target ? 0 : -1;
int l = 0, r = n - 1;
while (l int mid = (l + r) / 2;
if (nums[mid] == target) return mid;
if (nums[0] if (nums[0] 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
};
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
l, r = 0, len(nums) - 1
while l 2
if nums[mid] == target:
return mid
if nums[0] if nums[0] 1
else:
l = mid + 1
else:
if nums[mid] 1]:
l = mid + 1
else:
r = mid - 1
return -1
复杂度分析
-
时间复杂度： ，其中 为 数组的大小。整个算法时间复杂度即为二分搜索的时间复杂度 。
-
空间复杂度： 。我们只需要常数级别的空间存放变量。
上一篇：python高级-闭包-装饰器
下一篇：第二章 - Java与协程
评论
亲，登录后才可以留言！