Go 实现十大常见排序(附带原理解释)
2021-06-05 12:05
标签:for 循环 部分 就是 结束 解决 工作量 迭代 从后往前 没事 无论你使用哪种语言,从事哪个方向,在面试中算法基本上都是逃不掉的。也许你听说过技术过时或者语言过时,但你绝对没有听过算法过时。这一次我们来了解一下常见的排序算法,以及它们的时间复杂度,并使用代码实现它们。 冒泡排序(Bubble Sort)是一种非常简单直观的排序算法,就是从左到右依次比较两个相邻元素,如果左边元素大于右边元素,就将两者交换;如果左边元素小于等于右边元素,不进行任何操作。 可以看到思想还是非常简单的,就是相邻两个元素挨个比大小,如果左边大于右边就进行交换。这样走完一轮,我们能把最大的那个数放在最右边。 然后重复上面的过程,不过当我们比较完一轮之后,第二轮只需要比较从左到右的 N - 1 个元素即可(N 为数组长度),因为数组中最大的元素已经被选出来了,就没有必要在比了。 所以执行完第二轮就能把第二大的元素选出来,最终我们只需要执行 N - 1 轮即可,因为 N 个元素,走完 N - 1 轮之后剩余的那个一定是最小的。 整个过程就像冒泡一样,气泡大的不断往外窜,所以就叫冒泡排序。 我们看看如何使用 Go 来实现冒泡排序: 但是上面这个程序还有一个可以优化的点,比如我们面对的是一个近乎有序的数组: 对于上面这个数组,我们在遍历第一轮的时候,首先还是内层循环左右挨个比较,最终会将 8 放在 9 的左边,数组变成如下: 然后再遍历一轮的话,很明显我们就把整个数组排好了。也就是说此时排好整个数组只需要两轮的功夫,按照我们之前的逻辑需要进行 8 轮。只不过从第 3 轮开始,内层循环在比较的时候发现每一次左边元素都小于等于右边元素,所以 if 条件不满足、什么也不做。那么这样的话,我们就可以优化一下上面的程序: 此时程序依旧是可以正常执行的,只不过它只有在面对近乎有序的数组时才会具有明显优势。因为随着轮数的增加,内层循环所需要比较数组中的元素的个数会越来越少,如果数组不是近乎有序,这种级别的优化实际上没有太大意义。 所以我们可以得出,冒泡排序的时间复杂度在最好情况下是 \(O(n)\),此时数组本身就是有序的,外层循环只需要循环 1 次 即可;最坏时间复杂度是 \(O(n^2)\),此时数组恰好是逆序的。 至于平均时间复杂度也是 \(O(n^2)\),尽管我们知道里面的内层循环每一次会越跑越短,最终应该是 \(O(\frac{n^2}{2})\),但我们说 O 内的常数是不考虑的,所以平均时间复杂度依旧是 \(O(n^2)\)。 选择排序同样是一种非常简单直观的算法,它的思想如下: 假设数组中第 1 个元素最小,然后让剩余的 N - 1 个元素依次和数组第 1 个元素进行比较,如果比第 1 个元素小,那么就进行交换。这样就能把最小的元素放在第一个位置(索引为 0) 再假设数组中第 2 个元素是第 2 小,然后让剩余的 N - 2 个元素依次和数组第 2 个元素进行比较,如果比第 2 个元素小,那么就进行交换。这样就能把第 2 小的元素放在第 2 个位置 然后不断重复,显然跟冒泡一样,我们只需要找到前 N - 1 个最小的元素排好序之后,剩余的那个元素一定是最大的。 当然其实更好的做法并不是每次都进行交换,而是记住最小元素对应的索引,最后只需要交换一次即可。 我们看看如何使用 Go 来实现选择排序: 然后我们继续看看如何优化上面的代码,我们上面是只要 我们额外引入了一个变量,通过它来维护最小元素对应的索引,这样最后只需要经过一次交换即可。 显然选择排序的时间复杂度无论好坏,都是 \(O(n^2)\),因为内外层循环都要全部跑完才可以。 插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 首先从索引为 1 的位置开始,比较 s[1] 和 s[0],再从索引为 2 的位置开始,比较 s[2]、s[1]、s[0];然后从索引为 3 的位置开始,总之就是不断地从后往前,如果左边元素比右边元素大,那么两者进行交换。 比如:从索引为 5 的位置开始,如果 s[4] > s[5],那么两者进行交换;然后比较 s[3] 和 s[4],如果 s[3] > s[4] 那么继续进行交换,然后索引继续减 1 进行比较;但如果 s[3] 从动图中,我们看到元素在比较的时候并没有发生交换,而是不断地向右平移,当找到应该插入的位置时,最终只需要交换一次即可。当然我们先尝试一下交换,因为这样最直观。 我们看看如何使用 Go 来实现插入排序: 但是上面的函数可以写的更加精简一些: 当然上面两种写法本质上没有太大区别,甚至第一种还更加的直观,当然这不是重点。我们说每一次比较都伴随这元素之间的交换,但是最正确的做法应该是采用平移的策略: 元素平移尽管没有两个元素交换那么直观,但它的性能明显是更优的,所以可以结合动图多观察几遍。 这里我们也可以看出插入排序的平均时间复杂度是 \(O(n^2)\),最好时间复杂度是 \(O(n^2)\)。这里和冒泡也是类似的,都是在数组已经有序的情况下,时间复杂度可以达到 \(O(n)\)。只不过冒泡排序是:外层循环遍历 1 次,内层循环全部遍历;而插入排序是:外层循环全部遍历,内层循环遍历 1 次。 希尔排序是插入排序的一个改进版本,也称为缩小增量排序,既然它是插入排序的改进版,那就证明插入排序存在缺点。因为插入排序每次只能将数据移动一个位置,我们举个栗子。 假设我们现在移动 3,首先 3 和 7 交换,再 3 和 6 交换、3 和 5、3 和 4,最终才能排好;那么问题来了,我们能不能加速这个过程呢?希尔排序就是为了实现这一点,它的做法是将整个待排序的记录分隔成若干子序列分别排序,待整个序列基本有序时,再对全体记录进行排序。文字说明不是很好理解,假设数组有 10 个数,索引是 0 到 9,那么希尔排序是怎么做的呢? 对这 5 个子数组使用插入排序,然后缩小 gap。 对这两个数组继续使用插入排序,然后再缩小 gap,当 gap 等于 1 时,和原始的插入排序是一样的。 所以逻辑不难理解,插入排序是将 gap 设置为 1,每次和前面的元素进行比较。而希尔排序是将 gap 的初始值设置的大一些(一般是数组长度除以 2),然后每一次元素都和前 gap 个元素进行比较,此时可以看成是粗粒度的排序。通过不断缩小 gap,粒度不断变细,最终当 gap 为 1 时完全等价于插入排序,只不过经过前几轮的局部排序,此时的数组已经基本有序了。 我们看看如何使用 Go 来实现希尔排序: 所以我们上面的分组跨度分别为 5、2、1,而它们也被成为希尔排序的增量,增量的选择可以有多种,我们上面采用的增量逐步折半的方法正是希尔排序的作者提出的一种方法,因此也被成为希尔增量。 希尔排序利用分组粗调的方式减少了直接插入排序的工作量,使得算法的平均时间复杂度低于 \(O(n^2)\)。但是在某些极端情况下,希尔排序的最坏时间复杂度仍然是 \(O(n^2)\),甚至比直接插入排序更慢。 此时数组中有 8 个元素,按照我们之前的逻辑,希尔增量应该为 4、2、1,但当希尔增量为 4 和 2 的时候,每个子数组内部的所有元素都没有进行任何的交换。直到我们将增量缩减为 1 的时候,数组才会按照插入排序的方式进行调整。 所以对于上面这样的数组,希尔排序不仅没有减少工作量,返回增加了分组操作的成本。因此对于希尔排序而言,关键是需要选择一组合适的增量,最具代表性的是 和 Sedgewick 增量。 总之希尔排序不是一个稳定的算法。 在介绍归并排序之前,我们先来看一个问题:有两个各自排好序的数组,现在将它们合成一个整体有序的数组。 现在要将它们合在一起,得到: 这样下来,平均是 \(O(n)\) 的时间复杂度,肯定比直接合并再整体排序要快,因为这两个数组各自本身就是有序的。那么下面我们来看看如何使用 Go 来实现: 而以上这个过程,我们就称之为发生了一次归并。因此你应该猜到归并排序是怎么实现的了,采用的就是分治法。将一个数组分成多个小数组单独进行排序,然后再将这些排序之后的小数组组合起来。 分治法不仅体现在归并排序上,它也是解决问题的一种常用策略。将一个问题 "分" 成多个小问题递归求解,而 "治" 的阶段则是将 "分" 的阶段所得到的各个结果组合在一起。 对于归并排序而言,使用静态图要比动图更容易表达其含义: 整体看起来像是一棵树,因此我们可以采用递归的方式去实现,当然也可以采用迭代的方式去实现,这里我们使用递归。而对于归并排序而言,显然我们需要实现两步,一个是分、一个是合,而对于长度为 n 的数组,它们的递归深度都是 \(O(log n)\)。 下面我们来看看如何使用 Go 来实现归并排序: 归并排序是一种非常高效的排序,每次合并操作的平均时间复杂度是 \(O(n)\) ,而二叉树的深度为 \(O(log n)\),所以整体的平均时间复杂度为 \(O(nlog n)\)。 快速排序又是一种分而治之思想在排序算法上的典型应用,快速排序可以看成是在冒泡排序基础上的递归分治法,从名字上来看就知道它的速度很快。那么快速排序是怎么做的呢? 然后来看看如何使用 Go 实现快速排序: 快排的平均时间复杂度为 \(O(nlog n)\),但如果数组本身就是有序的、或者逆序的,那么会退化为 \(O(n^2)\),因为每一次 partition 之后一边都是空的。 Go 实现十大常见排序(附带原理解释) 标签:for 循环 部分 就是 结束 解决 工作量 迭代 从后往前 没事 原文地址:https://www.cnblogs.com/traditional/p/14624541.html楔子
冒泡排序

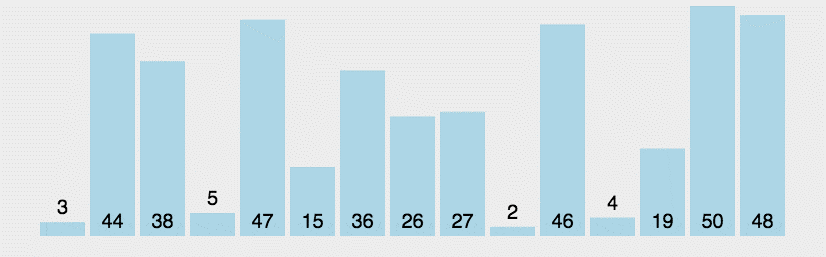
代码演示
package main
import (
"fmt"
"math/rand"
"time"
)
func bubbleSort(s []int) {
// 总共有 len(s) 个元素,只需要将前 len(s) - 1 个最大的元素排好即可
// 因此只需要遍历 len(s) - 1 次
for i := 0; i s[j+1] {
s[j], s[j+1] = s[j+1], s[j]
}
}
}
}
func main() {
var s = make([]int, 10)
rand.Seed(time.Now().UnixNano())
for i := 0; i [1, 2, 3, 4, 5, 8, 7, 6, 9][1, 2, 3, 4, 5, 7, 6, 8, 9]func bubbleSort(s []int) {
for i := 0; i s[j+1] {
s[j], s[j+1] = s[j+1], s[j]
// 在里面我们将其设置为 false
flag = false
}
}
// 如果数组没有排好序,那么进入上面的 if 语句之后,flag 会被设置成 false
// 如果数组已经排好序了,那么 flag 显然为 true,这里就可以直接 break 了
// 因此可以看出,如果排好序花了 3 轮,那么第 4 轮的时候才能跳出循环
if flag {
break
}
}
}
选择排序
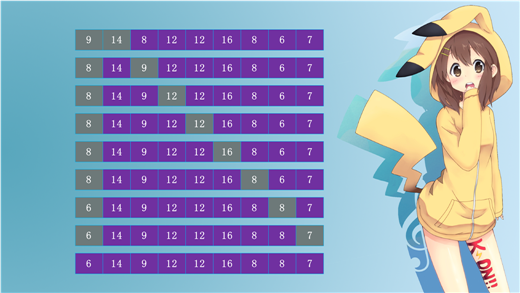
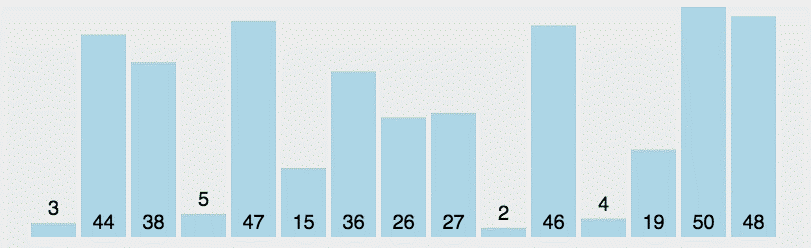
代码演示
package main
import (
"fmt"
"math/rand"
"time"
)
func selectSort(s []int) {
// 循环依旧遍历 len(s) - 1 次
for i := 0; i s[j] ,那么两者就进行交换。但是实际上,我们可以单独使用一个变量来维护这个最小元素对应的索引,循环结束是只需要做一次交换即可。func selectSort(s []int) {
for i := 0; i 插入排序

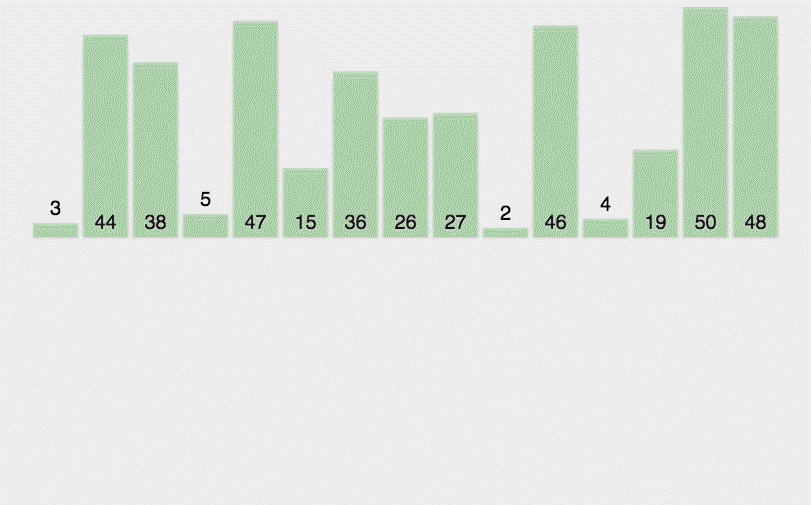
代码演示
package main
import (
"fmt"
"math/rand"
"time"
)
func insertSort(s []int) {
// 外层循环从 1 开始,不断遍历
for i := 1; i = 1; j-- {
// 如果 s[j - 1] > s[j],证明这两个元素应该发生交换了
if s[j-1] > s[j] {
s[j], s[j-1] = s[j-1], s[j]
} else {
// 否则说明不需要发生交换,根据我们之前的结论,此时就已经排好了,应该直接将内层循环 break 掉
break
}
}
}
}
func main() {
var s = make([]int, 10)
rand.Seed(time.Now().UnixNano())
for i := 0; i func insertSort(s []int) {
for i := 1; i = 1 && s[j-1] > s[j]; j-- {
s[j], s[j-1] = s[j-1], s[j]
}
}
}
func insertSort(s []int) {
for i := 1; i = 1 && s[j-1] > tmp; j-- {
s[j] = s[j-1]
}
// 接下来 j 不断自减,只要 s[j-1] > tmp 就向右平移
// 如果 s[j-1] 希尔排序
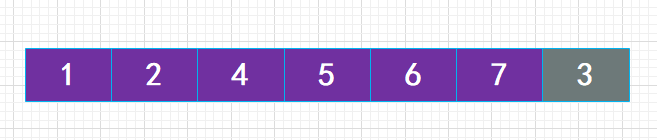
第一步: gap 等于 5(数组长度除以 2),相当于分成了 5 个子数组,分别是[0, 5]、[1, 6]、[2, 7]、[3, 8]、[4, 9](里面是元素对应的索引)第二步:gap 等于 2(上一步的 gap 除以 2),此时相当于分成了两个子数组,分别是[0, 2, 4, 6, 8]、[1, 3, 5, 7, 9]第三步:gap 等于 1(上一步的 gap 除以 2),此时和原本的插入排序是一样的了,就是整个数组。但是注意,此时的数组已经整体接近有序了,所以接下来再排序就简单多了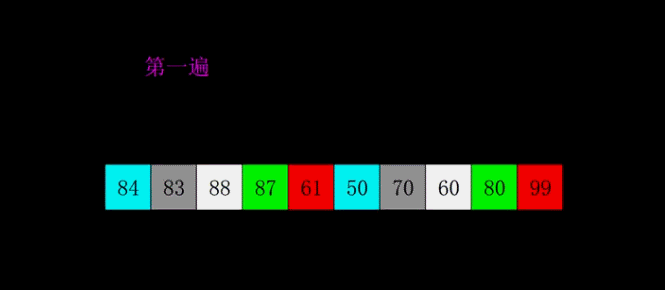
代码演示
package main
import (
"fmt"
"math/rand"
"time"
)
func shellSort(s []int) {
// gap 初始值为 len(s) / 2
gap := len(s) / 2
// 显然外面要多一层循环,当 gap >= 1 时
for gap >= 1 {
// 此时 i 从 gap 开始
for i := gap; i = gap && s[j-gap] > tmp; j-=gap {
s[j] = s[j - gap]
}
// 可以看到整体和插入排序是一样的
s[j] = tmp
}
// gap 每次除以 2
gap /= 2
}
}
func main() {
var s = make([]int, 10)
rand.Seed(time.Now().UnixNano())
for i := 0; i 
归并排序
[1, 3, 4, 5, 7] 和 [2, 3, 6, 8, 9][1, 2, 3, 3, 4, 5, 6, 7, 8, 9],虽然很简单,但如果我们要求时间复杂度为 \(O(n)\) 呢?会发现还是需要动一些脑子的。当然解决办法也很简单,采用双指针即可: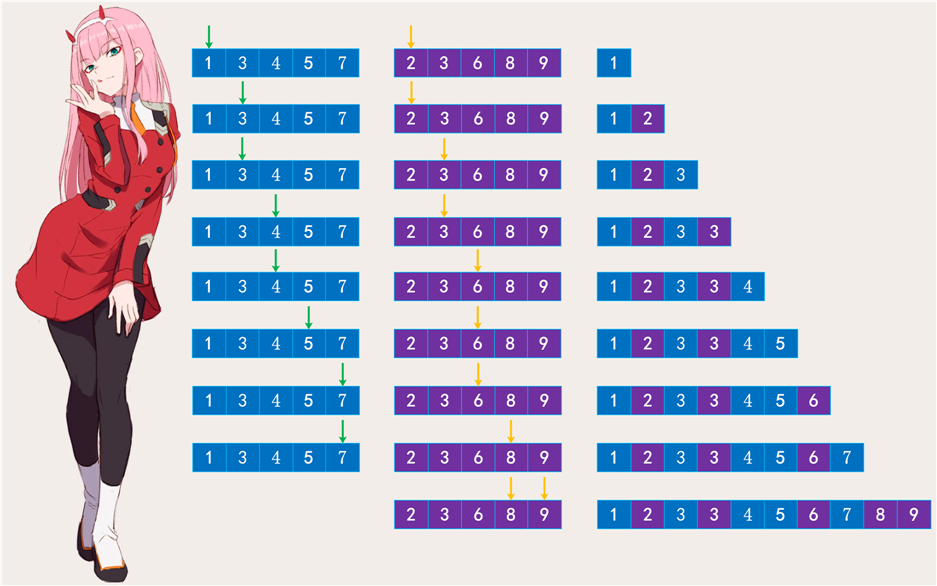
package main
import "fmt"
func merge(s1 []int, s2 []int) []int {
var s1Len, s2Len = len(s1), len(s2)
// 显然我们需要新开一个数组,长度为两个数组的长度之和
var mergeS = make([]int, s1Len+s2Len)
// 设置遍历用的索引,i 负责遍历 s1、j 负责遍历 s2
var i, j int
for i, j = 0, 0; i
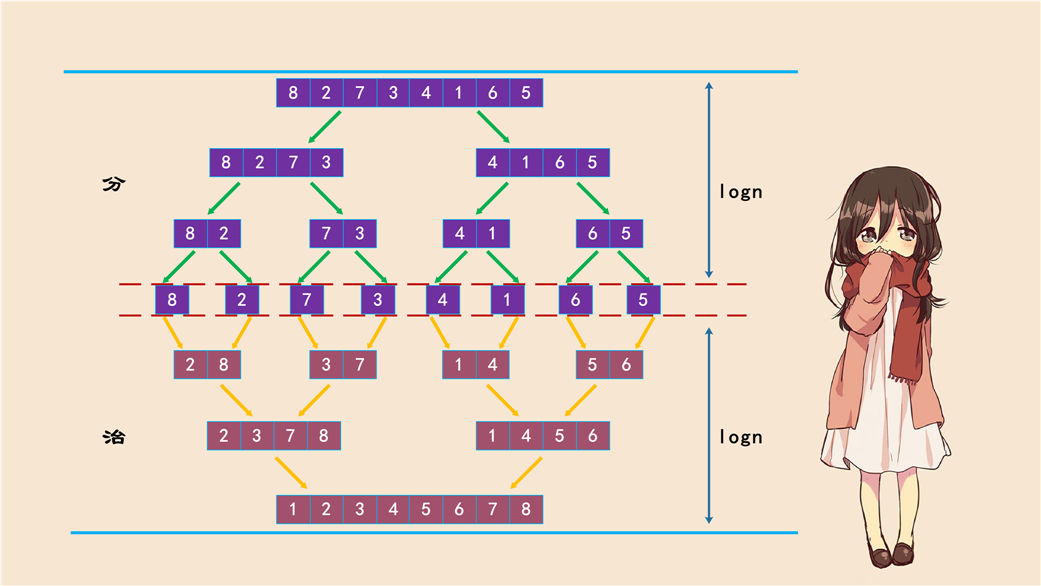
package main
import (
"fmt"
"math/rand"
"time"
)
// 这部分代码保持不变
func merge(s1 []int, s2 []int) []int {
var s1Len, s2Len = len(s1), len(s2)
var mergeS = make([]int, s1Len+s2Len)
var i, j int
for i, j = 0, 0; i 快速排序
1. 从数列中挑出一个元素,称为 "基准"(pivot)2. 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任意一边),该过程称为分区(partition)操作3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列重复第 2 步package main
import (
"fmt"
"math/rand"
"time"
)
func partition(s []int, left, right int) int {
// 设置基准值以及索引
var pivot, pivotIndex = s[left], left
// 要使得左边的元素比基准值小,右边的元素比基准值大
for left = pivot {
// 如果 s[right] >= pivot,直接 right 左移
right--
}
for left 未完待续
上一篇:Spring Data JPA