面向对象第一单元总结:Java实现表达式求导
2021-06-07 09:03
标签:题目 res oid 解题思路 面向对象的思想 计算 需要 递归 inpu 本人采用递归下降的思路,下面简述递归下降算法: 假设一个类A的字符串形式是 这样,从最大的一级,逐级递归的找更小的构成单元,直到找到以字符为匹配单元的最小单元,由此可以对符合一定语法的字符串进行全面分析 现在再看,我设计的递归下降其实糅合了递归下降和类的生成,这就使得耦合度过高,较为高明的办法应该是使用工厂模式,建立一个 由于在递归下降的过程中,经常需要移动指针、判断字符,因此将这部分功能抽取出来作为一个新的工具类,减小递归下降类的复杂度 成员由一个 这样的设计,减少了递归下降过程中代码的重复,增加了可读性,使思路更加明晰 实现了上面描述的递归下降算法,不再赘述,复杂度如下 由于需要分析各种不同类型的格式错误,因此不可避免的在某些方法中的判断语句过多 自定义的异常类,继承自 虽然只需要输出一个 类内虽然只有几行,但也是符合面向对象的代码: 为了放置和内置库冲突,在自定义的类之前加一个M表示My 其基本形式是许多项的和,因此也可以看成是一个项的累加类 成员只有一个项的 类的主要方法如上,可以看到每一个方法都较为简短 由于 需要注意的是: 到得到 其中有一些小小的细节需要考虑,比如项的第一个字符需要是正负号 因此函数体为 在 我们需要遍历已有的 相信这几个例子就能够展现面向过程的魅力了。一个类不会过多的考虑除了自己意外的细节,把能交给别人做的事情都交给别人,自己只管提出需求。这样写代码会思路清晰,维护简单且可读性好 其基本形式是许多因子的成绩,因此也可以看成是一个因子的累乘类 成员只有一个因子的 绝大部分方法依然比较简短,只有在判断两个项是否需要合并时较为复杂,不具有普遍意义 具体的实现就不再赘述,与 幂函数主要由指数组成,我的设计中没有“变量”这一个概念,而是用幂函数来代替“变量”,其他的如\(sin(x)**2\)不是幂函数,而是三角函数,三角函数自己有一个指数 因此,如果要增加多变量求偏导数的需求,只需要更改 细节不再赘述,其复杂度如下。可以看到也较为简单 一个 其余不再赘述,复杂度如下 面向对象编程的一大特点就是——bug少,而且容易找到。编写内核代码的过程十分顺畅,且几乎不产生bug,即使有,也很快就能找得出。 我认为,原因就在于面向对象编程时,会将一个任务分解成一个个小任务,并且任务之间的耦合度比较低 比如说,我需要完成“表达式求导”这一项任务,那么一个 这五个步骤几乎不涉及到任何的细节问题,而是对任务做出规划,因此这一段代码出bug的概率极低 这样一层一层的将任务细化,最终只有很少部分的方法需要考虑细节问题,大大降低了bug的可能性 面向对象第一单元总结:Java实现表达式求导 标签:题目 res oid 解题思路 面向对象的思想 计算 需要 递归 inpu 原文地址:https://www.cnblogs.com/beityluo/p/14587894.html面向对象第一单元总结:Java实现表达式求导
题目要求
思路分析
表达式拆解
Polynomial、项Term、因子Unit
解题思路
字符串->表达式
"BCD"(拼接),B的形式是"x*E",c是sin(x),D是(A),E是+,那么我们要分析字符串A,就可以这样写 public A getA(){
A ans = new A();
B newB = getB();
C newC = getC();
D newD = getD();
ans.addB(newB); ans.addC(newC); ans.addD(newD);
return ans;
}
public B getB(){
B ans = new B();
if(接下来是"x*"){
走2步;
} else {
throw 格式错误异常;
}
E newE = getE();
ans.addE(newE);
return ans;
}
public C getC(){
C ans = null;
if(接下来是"sin(x)"){
ans = new C();
走6步;
} else {
throw 格式错误异常;
}
}
public D getD(){
D ans = null;
if(接下来是"("){
走1步;
} else {
throw 格式错误异常;
}
A newA = getA();
ans.addA(newA);
if(接下来是")"){
走1步
} else {
throw 格式错误异常;
}
return ans;
}
...//剩下的就不写了,主要思路已经阐释清楚
MFactory类,在递归下降中,将匹配到的字符串交由工厂生成一个相应的对象,而不是自己new一个出来递归下降用到的类
ExpressionString
String存放表达式,一个Integer存放当前位置ExpressionString实现的方法主要是 public void moveSpace(); //跳过当前位置向后的空格
public void moveForward(int step); //位置向前移动step步
public boolean isEnd(); //判断是否读到字符串末尾
public boolean isStartWithChar(char c); //判断是否以c字符开头
public boolean isStartWithString(String s); //判断是否以s字符串开头
...
ExpressionParser
Method
CogC
ev(G)
iv(G)
v(G)
ExpressionParser.ExpressionParser(String)0.0
1.0
1.0
1.0
ExpressionParser.getConstant()0.0
1.0
1.0
1.0
ExpressionParser.getCos()18.0
8.0
10.0
11.0
ExpressionParser.getMultiplicationSign()3.0
3.0
3.0
3.0
ExpressionParser.getOperator()4.0
4.0
4.0
4.0
ExpressionParser.getPoly()1.0
1.0
2.0
2.0
ExpressionParser.getPolyUnit()2.0
2.0
2.0
2.0
ExpressionParser.getPower()12.0
5.0
7.0
8.0
ExpressionParser.getSignedInteger()6.0
3.0
3.0
5.0
ExpressionParser.getSin()18.0
8.0
10.0
11.0
ExpressionParser.getTerm()3.0
1.0
4.0
4.0
ExpressionParser.getUnit()7.0
6.0
8.0
8.0
ExpressionParser.isEnd()0.0
1.0
1.0
1.0
Total
74.0
44.0
56.0
61.0
Average
5.6923076923076925
3.3846153846153846
4.3076923076923075
4.6923076923076925
InputWongFormatException
Exception,用于在检测到输入格式错误时抛出异常WONG FORMAT!!!,但也要符合面向对象的设计,Java的抛出异常机制非常实用,建议好好学习一下 private String exceptionInfor;
public InputWrongFormatException() { //在构造函数中初始化,这样方便应对未来多变的需求
exceptionInfor = "WRONG FORMAT!";
}
public String getExceptionInfor() { //不要将错误信息设置为public,而是留下相应的方法
return exceptionInfor; //这样外部只需要System.out.println(e.getExceptionInfor());即可
}
内核各个类的创建、思路分析
类图:
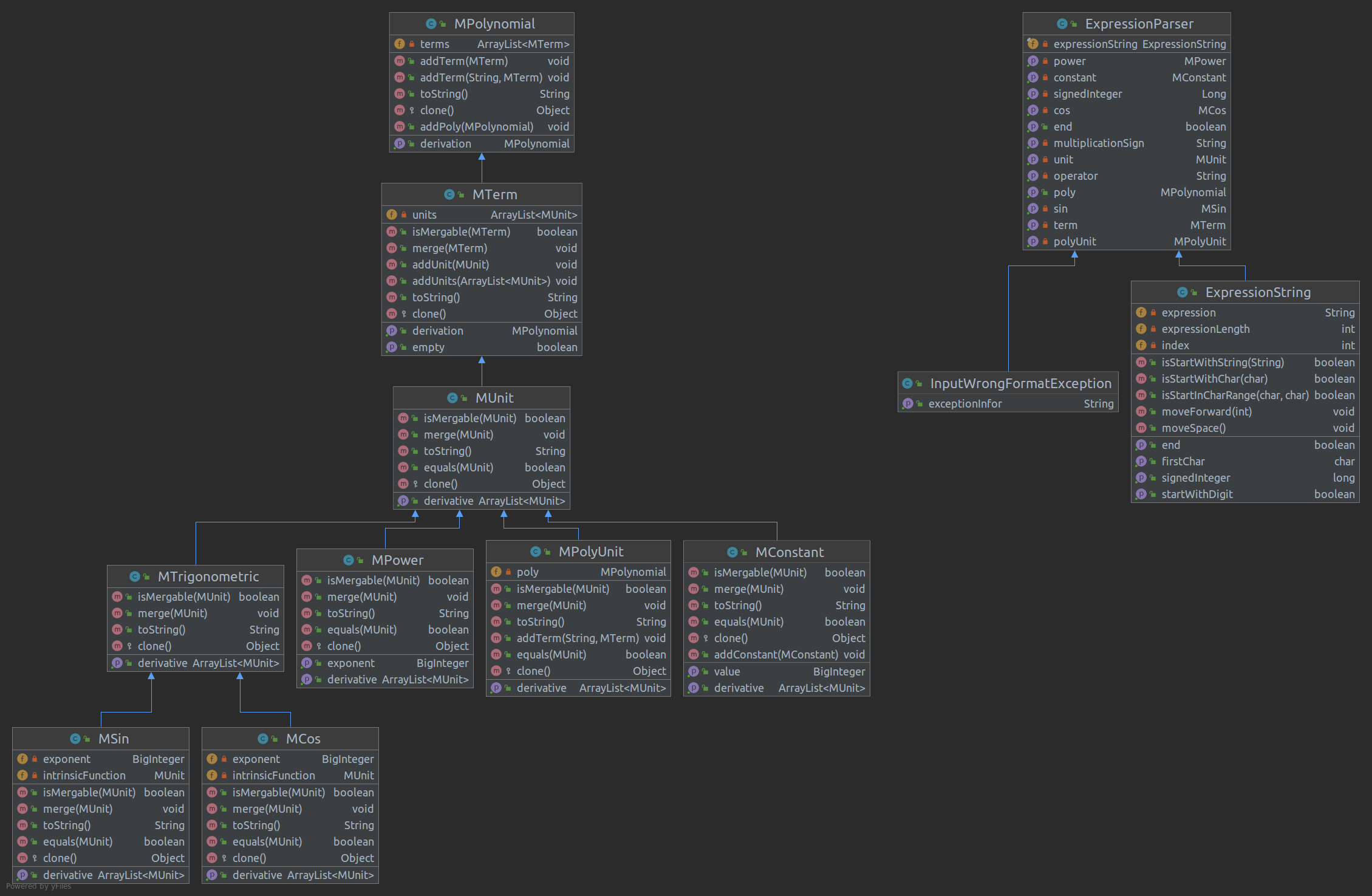
MPolynolmial(多项式)
MPolynomial类代表了一整个表达式ArrayList
Method
CogC
ev(G)
iv(G)
v(G)
MPolynomial.addPoly(MPolynomial)8.0
4.0
5.0
5.0
MPolynomial.addTerm(MTerm)4.0
3.0
4.0
4.0
MPolynomial.addTerm(String,MTerm)2.0
1.0
3.0
3.0
MPolynomial.clone()2.0
1.0
3.0
3.0
MPolynomial.getDerivation()1.0
1.0
2.0
2.0
MPolynomial.MPolynomial()0.0
1.0
1.0
1.0
MPolynomial.toString()6.0
1.0
4.0
6.0
Total
23.0
12.0
22.0
24.0
Average
3.2857142857142856
1.7142857142857142
3.142857142857143
3.4285714285714284
下面以
MPoly中的几个方法说明面向对象的思想
getDerivation()
MPoly是一个累加类,因此他的导数就等于各个项的导数的和,因此函数体为 MPolynomial poly = new MPolynomial();
for (MTerm term : terms) {
MPolynomial derivation = term.getDerivation();
poly.addPoly(derivation);
}
return poly;
MPoly类不会考虑如何得到一个项的导数,他会把这项任务交给一个MTerm(项)去做,MPoly只管跟一个MTerm要他的导数MPoly的导数依旧是一个MPoly,因为\((a+b)‘=a‘+b‘\)依旧是一个多项式,只有在Main函数的最后输出时,再调用MPoly的toString()方法获得字符串形式toString()
MPoly的字符串形式,只需要获得每一项的的字符串,并拼接起来即可 String ans = "";
for (MTerm term : terms) { //最重要的6行代码
String next = term.toString();
if (!next.equals("+0") && !next.equals("0")) { //小优化:如果Term是0,则跳过
ans += next;
}
}
if (ans.equals("")) { //如果到最后还是0,则ans为“0”
ans = "0";
}
if (ans.charAt(0) == ‘+‘) { //如果第一个字符为‘+‘,则删掉
ans = ans.substring(1);
}
return ans;
addPoly()
getDerivation()中,我们得到的每一个MTerm的导数都是一个MPoly,每一次需要将新的多项式加到已有的多项式中,因此需要一个addPoly(MPolynomial newPoly)方法MTerm,每一次再遍历新的newPoly的所有项,如果两个项能够合并,就合并他们(这其实是一个优化过程,也可以不判断直接加到MTerm的ArrayList中),因此函数体为 for (MTerm newTerm : poly.terms) {
boolean foundMergableTerm = false; //记录是否找到了一个可以合并的项
for (MTerm term : terms) {
if (term.isMergable(newTerm)) {
term.merge(newTerm);
foundMergableTerm = true;
break;
}
}
if (!foundMergableTerm) {
terms.add(newTerm);
}
}
MTerm(项)
MTerm类代表了一个类ArrayList
Method
CogC
ev(G)
iv(G)
v(G)
MTerm.addUnit(MUnit)4.0
3.0
4.0
4.0
MTerm.addUnits(ArrayList)1.0
1.0
2.0
2.0
MTerm.clone()2.0
1.0
3.0
3.0
MTerm.getDerivation()6.0
1.0
4.0
4.0
MTerm.isEmpty()0.0
1.0
1.0
1.0
MTerm.isMergable(MTerm)16.0
4.0
5.0
8.0
MTerm.merge(MTerm)10.0
6.0
2.0
6.0
MTerm.MTerm()0.0
1.0
1.0
1.0
MTerm.toString()9.0
3.0
4.0
8.0
Total
48.0
21.0
26.0
37.0
Average
5.333333333333333
2.3333333333333335
2.888888888888889
4.111111111111111
MPolynomial的思想是完全相同的,将更基础的事交给底下的MUnit(因子)去做MUnit(因子)
MUnit是所有因子的父类,可以定义为一个抽象类或者是借口,因为我们不需要创建一个MUnit对象,只会创建如cos,sin,x**2等因子对象MUnit规定子类需要实现的方法有:
public ArrayListMConstant(常数因子)
MPower(幂函数)
MPower类的内容,增加成员“变量”,并修改求导、求字符串等函数即可
Method
CogC
ev(G)
iv(G)
v(G)
MPower.clone()0.0
1.0
1.0
1.0
MPower.equals(MUnit)1.0
1.0
2.0
2.0
MPower.getDerivative()0.0
1.0
1.0
1.0
MPower.getExponent()0.0
1.0
1.0
1.0
MPower.isMergable(MUnit)0.0
1.0
1.0
1.0
MPower.merge(MUnit)0.0
1.0
1.0
1.0
MPower.MPower(BigInteger)0.0
1.0
1.0
1.0
MPower.MPower(BigInteger,MUnit)0.0
1.0
1.0
1.0
MPower.MPower(String)0.0
1.0
1.0
1.0
MPower.toString()3.0
1.0
3.0
3.0
Total
4.0
10.0
13.0
13.0
Average
0.4
1.0
1.3
1.3
MTrigonometric(三角函数)
MCos和MSin的父类,只是为了增加程序的扩展性,在这三次作业中没起到任何作用,也没有任何有意义的、与MUnit不重复的方法MSin(sin函数) MCos(cos函数)
BigInteger成员作为指数,一个MUnit成员作为内函数(只有第三次作业从单独的x变为一个因子)
Method
CogC
ev(G)
iv(G)
v(G)
MSin.clone()1.0
1.0
2.0
2.0
MSin.equals(MUnit)1.0
1.0
3.0
3.0
MSin.getDerivative()1.0
1.0
2.0
2.0
MSin.isMergable(MUnit)1.0
1.0
2.0
2.0
MSin.merge(MUnit)0.0
1.0
1.0
1.0
MSin.MSin()0.0
1.0
1.0
1.0
MSin.MSin(BigInteger,MUnit)0.0
1.0
1.0
1.0
MSin.toString()3.0
1.0
3.0
3.0
Total
7.0
8.0
15.0
15.0
Average
0.875
1.0
1.875
1.875
MPolyUnit(表达式因子)
MPolyUnit只有一个MPolynomial成员,两者的本质区别就在于,MPolyUnit继承自MUnit,以及比MPolynomial在toString()中两侧套了一组括号,其余方法均直接调用MPolynomial的同名方法程序中的bug
MPoly需要做的就是以下几步:
测评中出现的bug
发现别人程序bug
重构经历总结
心得体会