浅谈 拓扑排序
标签:有关 邻接表 char string ++ 循环 getch etc ==
我是什么时候想到要学拓扑排序的呢?
在一次模考的时候,有这样一道题,叫做食物链,我是写了记忆化搜索的,然而全场都写了拓扑板子
后来发现我居然不会这么基础的算法,有点慌
下面进入正题
拓扑排序是针对一些特殊问题的,类似于在完成某一件是之前,有必要条件,要先完成另外的一些任务
只有有向无环图才有拓扑排序,这就关系到了定义
拓扑排序是先排入度为零的点,然后把所有的与之有关的边都删掉,这时就又会有一些如度为零的点出现
然以后循环上述操作
这就是拓扑排序的基本概念
还是举个例子吧
如图:
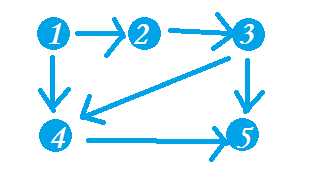
我们发现1的如度为零
所以先把1删掉,把与1有关的边删掉

然后就发现2的入度变成了零
然后会重复上述操作
得到了这个图的与拓扑排序:1 2 3 4 5
下面给出代码:
#include
#include
#include
#include
#include
#includestring>
#include
using namespace std;
inline int min(int a,int b){return aa:b;}
inline int max(int a,int b){return a>b?a:b;}
inline int rd()
{
int x=0,f=1;
char c=getchar();
for(;!isdigit(c);c=getchar()) if(c==‘-‘) f=-1;
for(;isdigit(c);c=getchar()) x=x*10+c-‘0‘;
return x*f;
}
inline void write(int x)
{
if(x0) putchar(‘-‘),x=-x;
if(x>9) write(x/10);
putchar(x%10+‘0‘);
}
int n,m;
int head[100006],nxt[100006],to[100006];
int in[100006];
int total=0;
void add(int x,int y){//邻接表存边
total++;
in[y]++;
to[total]=y;
nxt[total]=head[x];
head[x]=total;
return ;
}
int tot=0;
int s[100006];
void topo(){
for(int i=1;iif(!in[i]) s[++tot]=i;//先找出已有的入度为零的点
for(int i=1;i){
for(int e=head[s[i]];e;e=nxt[e]){//删除与其相关的边
in[to[e]]--;
if(!in[to[e]]) s[++tot]=to[e];//如果又出现入度为零的点,就入队
}
}
return ;
}
int main()
{
n=rd(),m=rd();
for(int i=1;i){
int x=rd(),y=rd();
add(x,y);//有向图单向存边
}
topo();
for(int i=1;i"%d\n",s[i]);
return 0;
}
可算是填了坑QAQ
浅谈 拓扑排序
标签:有关 邻接表 char string ++ 循环 getch etc ==
原文地址:https://www.cnblogs.com/WWHHTT/p/9716347.html
文章来自:
搜素材网的
编程语言模块,转载请注明文章出处。
文章标题:
浅谈 拓扑排序
文章链接:http://soscw.com/essay/95455.html
评论

