算法的时间复杂度比较,计算多项式的直接法和秦九韶法
2021-06-18 14:16
标签:比较 .com print 利用 数量级 复杂 算法 设置 mat 1.直接法: 每次循环迭代,pow函数内部都会执行i次乘法,然后一次加法,所以整体的算法复杂度为O = 1/2 * n ^ 2 + 3/2n,尽管pow函数的实现方法是利用递归优化后的,但是算法复杂度还是达到了O(nlogn) 2.秦九韶法: 它不断提取公因式x来减少乘法的运算次数,算法复杂度为O(n); 下面介绍一个测试运行时间的函数 clock()函数可以捕捉从程序开始运行到clock()被调用时所打下的点数,在要测试的函数前后各放置一个clock()函数,利用两个clock()函数即可计算出执行一个函数所打下的点数,CLK_TCK(或者是CLOCKS_PER_SEC)是一个常量,表示一个机器时钟每秒钟所打下的点数,简单计算后即可得到测试函数的运行时间,但是因为一个函数的运行时间是在是太短了,短到时钟还来不及打下下一个点函数就运行结束了,所以我们让被测函数重复循环多次执行,即可得到特定次数下的运行时间,被测函数的运行时间的比较就可以实现了。 下面是主函数,设置了多项式的各项系数 根据MAXK设置不同的值,让被测函数重复循环执行相应的次数,实验结果如下 10^4: 10^6: 由实验结果可以看出,秦九韶算法几乎都比普通算法快一个数量级 算法的时间复杂度比较,计算多项式的直接法和秦九韶法 标签:比较 .com print 利用 数量级 复杂 算法 设置 mat 原文地址:https://www.cnblogs.com/hi3254014978/p/9707051.html1 double Polynomial_1(int n, double a[], double x)
2 {
3 int i;
4 double sum = 0;
5 for (i = 0; i )
6 sum += a[i] * pow(x, i);
7 return sum;
8 }
1 double Polynomial_2(int n, double a[], double x)
2 {
3 int i;
4 double sum = 0;
5 for (i = n; i > 0; i--)
6 sum = a[i - 1] + x * sum;
7 return sum;
8 }
1 void run(double(*f)(int, double*, double), double a[], int case_n)
2 {
3 //此函数用于测试被测函数(*f)的运行时间,并且根据case_n输出相应的结果
4 //case_n是输出的函数编号,1代表Polynomial_1, 2代表Polynomial_2
5 int i;
6 start = clock(); //开始计时
7 for (i = 0; i //重复调用函数已获得充分多的时钟打点数
8 (*f)(MAXN, a, 1.1);
9 stop = clock(); //结束计时
10 duration = ((double)(stop - start)) / CLK_TCK; //计算运行时间
11 printf("ticks %d = %f\n", case_n, (double)(stop - start));
12 printf("duration 1 = %6.2e\n", duration);
13 }
1 #include
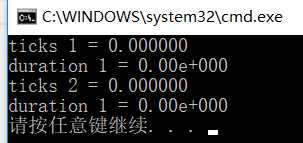 10^5:
10^5: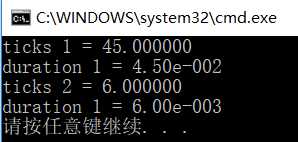
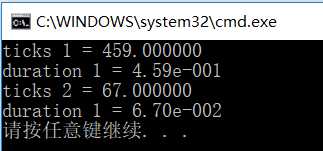 10^7:
10^7: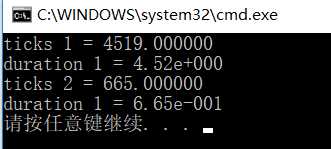
下一篇:JAVA语言程序设计(一)(1)