使用Python求牛顿插值多项式及其差商表

 1 import numpy as np
 2 from sympy import *
 3 
 4 # 定义一个求差商表的函数，使用递归求解差商表，返回值是差商的值
 5 # x是数组，表示样本点的x
 6 # f是数组，表示样本点的函数值f（x）
 7 # start是int类型，表示x数组的起始下标，
 8 # end是int类型，表示x数组的结束下标，
 9 # res是数组类型，表示差商表，对角线以下为各阶差商表
10 def cs(x,f,start,end,res):
11     # 当x中只有两个元素的时候，结束递归
12     if((end-start)==1):
13         # 将一阶差商填入差商表
14         res[end-1][end-start-1]=(f[end]-f[start])/(x[end]-x[start])
15         # 返回差商
16         return res[end-1][end-start-1]
17     # 当x中元素个数大于2时，根据公式递归调用此函数求差商，并将差商填入差商表
18     res[end-1][end-start-1]=(cs(x,f,start+1,end,res)-cs(x,f,start,end-1,res))/(x[end]-x[start])
19     # 返回差商
20     return res[end-1][end-start-1]
21 
22 # 定义一个求牛顿插值多项式的函数
23 # x是数组，表示样本点的x
24 # f是数组，表示样本点的函数值f（x）
25 def Newton(x,f):
26     res = np.ones([x.size - 1, x.size - 1])*np.inf # 初始化差商表骨架结构
27     cs(x, f, 0, x.size - 1, res) #调用差商表函数给差商表填值，对角线及以下才是差商表的值
28     X=symbols("x") #定义x变量
29     y=f[0] #初始化牛顿插值多项式，它的第一项是常数项，正好是f[0]
30     for i in range(x.size-1):
31         temp=1 #临时变量，保存  f[x0,x1,...,xn]*(x-x1)(x-x2)...(x-xn-1)
32         for j in range(i+1):
33             temp=temp*(X-x[j]) #(x-x1)(x-x2)...(x-xn-1)
34         temp=res[i,i]*temp #将差商表对角线元素作为系数
35         y=y+temp #将temp添加到多项式中
36     # 返回牛顿插值多项式
37     return y
38 
39 if __name__=="__main__":
40     # 样本点
41     x=np.array([2.0,2.1,2.2,2.3,2.4])
42     f=np.array([1.414214,1.449138,1.483240,1.516575,1.549193])
43 
44     ##### 可以直接得到差商表
45     res = np.ones([x.size - 1, x.size - 1]) * np.inf  # 初始化差商表骨架结构
46     # 调用差商表函数
47     cs(x,f,0,x.size-1,res)
48     print(res)
49 
50     #### 也可以直接得到牛顿插值多项式
51     X=symbols("x") #定义自变量x
52     y=Newton(x,f) #调用函数得到牛顿插值多项式，类型是
53     print("N(x)=",y)
54     # 给自变量x赋值，求出函数近似值
55     print(y.evalf(subs={X:2.15})) #求给定自变量x值时函数f(x)的值 | 将表达式转化为函数

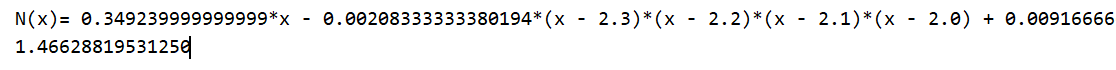
 1 #拉格朗日插值法
 2 def L(x,f):
 3     X=symbols("x")
 4     m=x.size #x个数
 5     L=0
 6     for i in range(m):
 7         temp=1
 8         for j in range(m):
 9             if(i!=j):
10                 temp=temp*((X-x[j])/(x[i]-x[j]))
11         L=L+temp*f[i]
12     return L