四则运算(二叉树实现) Java
2021-06-22 08:04
标签:add 出现 没有 分数类 Plan poi xtend 机构 ash GitHub仓库 我们平常见到的表达式:1+2×3÷(4-5)+6是一种中缀表达式,转化为后缀表达式就是123×45-÷+6+,还有一种前缀表达式就详细说了。一条表达式就可以用一颗二叉树来表示,这个种表达式树定义以下性质 无论前缀,中缀,还是后缀,只是访问的时机不一样,上面表达式转化为二叉树就是 绿色为符号节点,红色为数字节点,所以如果限定符号节点数不超过3个,那就是用随机函数,随机生成一个数,在构建一棵子树的时候应该算出子树的结果和树高 负数的产生是因为减法运算,在上面的算数中4-5会产生负数,在计算符号节点的结果的时候,需要判断一下结果是否是负数,如果是负数,就取绝对,就是将左右子树互换就行 表达式1+2×3÷(4-5)+6在计算4-5的时候发现是-1,然后对调左右子树,就相当于取了绝对值 我的思路就是将整数,也当做分数来计算,然后在输出的时候将分数转化为整数,或者分数的形式,然后定义一个类来表示分数,这个类应该有加减乘除的方法,并且在运算的过程中需要保证最简 递归判断两棵表达式树k1,k2, 如果k1->left == k2->left && k1->right == k2->right,然后就可以判定k1,k2是两棵相同的树,也就是表达式一样,如果不相同并且符号是+或者×的时候,就判断k1->left == k2->right && k1->right == k2->left ,如果满足,也是相同的一个表达式树,其他都是不相同的树,比如 1+2×3÷(5-4)+6 跟 6+3×2÷(5-4)+1 就是一样的表达式 定义一个分数类,里面应该需要加减乘除 表达式里面有两个内部类来表示节点 叶子节点是分数节点:Node 非叶子节点就是符号节点:SymbolNode 构建表达式 第一种构建方式就是给定非叶子结点的数量,随机生成 第二种就是给定特定的中缀表达式来构建 输出表达式到Exercises.txt和输出答案到Answers.txt 根据给定的表达式和结果输出正确的题数和错误的题数 随机输出10条20范围以内的表达式和答案 得到测试结果: 表达式: 结果: 随机输出10000条20范围以内的表达式和答案: 由于太多,给个连接打开 点击我查看10000条表达式 点击查看答案 对比上面输出的10条表达式和答案,结果 然后故意修改第2道题的结果为100,和第7道题为50,然后再重新运行一遍,结果如下 然后对比10000道题的结果,其中我在答案文件中,随机改变了正确的数值,得到以下对比结果 点击查看10000道题目的对比结果 与柯文朗同学一起讨论编写程序,我主要负责写代码,然后我们一起讨论,有时候自己卡住的时候,别人的建议会让自己思维变得更加清晰,在写代码的过程中,两个人的思维碰撞会产生意外的结果,有一些细节的地方自己没有办法想到,就可以由另外一个人填补,两个人提高了程序的设计与编写的速度,我们在讨论如果碰到负数的时候应该怎么办的时候,我的想法本来是将减号换为加号,虽然可行,但是在一定程度上干扰了随机生成符号的这设计理念,在我犹豫的过程中,柯文朗同学提出取绝对值得想法,将左右两个表达式互换,最终商讨觉得他的想法比较好,然后采纳了他的想法 四则运算(二叉树实现) Java 标签:add 出现 没有 分数类 Plan poi xtend 机构 ash 原文地址:https://www.cnblogs.com/pramy/p/9678594.html四则运算
功能
设计
表达式:
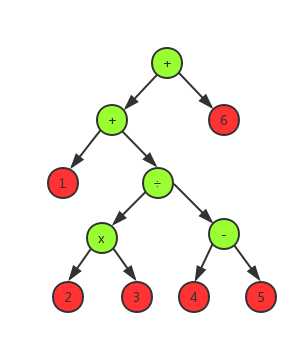
负数:
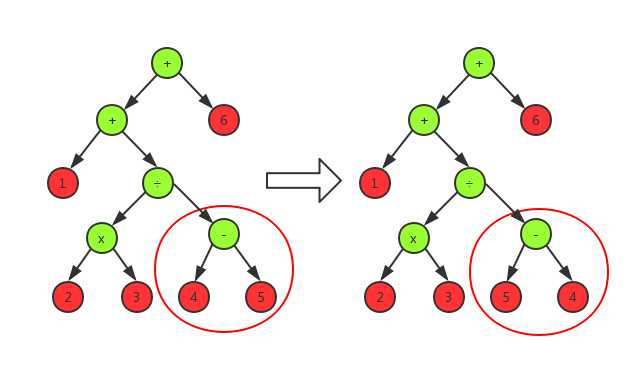
分数,整数的表示
判断是否重复
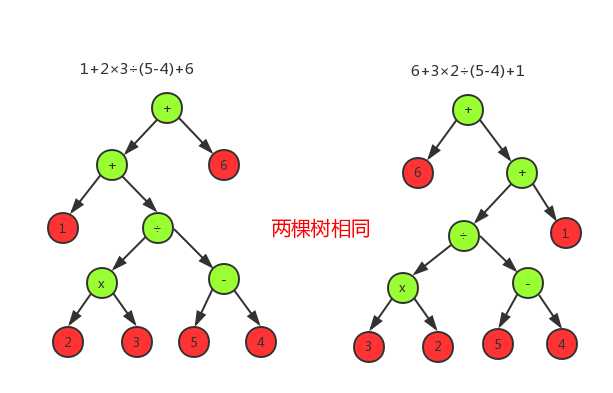
代码
分数:Fraction
/**
* IntelliJ IDEA 18
* Created by Pramy on 2018/9/16.
*/
public class Fraction {
/**
* 分子
*/
private int a;
/**
* 分母
*/
private int b;
public Fraction(String string) {
string = string.trim();
int a, b;
int cc = string.indexOf("‘");
int bb = string.indexOf("/");
if (cc != -1) {
int c = Integer.valueOf(string.substring(0, cc));
b = Integer.valueOf(string.substring(bb + 1));
a = c * b + Integer.valueOf(string.substring(cc + 1, bb));
} else if (bb != -1) {
b = Integer.valueOf(string.substring(bb + 1));
a = Integer.valueOf(string.substring(0, bb));
} else {
a = Integer.valueOf(string);
b = 1;
}
adjust(a,b);
}
public Fraction(int a, int b) {
adjust(a,b);
}
private void adjust(int a, int b) {
if (b == 0) {
throw new RuntimeException("分母不能为0");
}
//记录负数的标志
boolean isNegative = false;
if ((a 0) || (a > 0 && b 表达式:Expression
static class Node implements Cloneable {
//表达式结果
Fraction result;
Node right;
Node left;
int high;
//```以下省略
}static class SymbolNode extends Node {
//符号
String symbol;
} /**
* 根据符号数来随机构造表达树
* @param sum 符号数
* @return node
*/
private Node build(int sum) {
//如果是0就构造叶子节点
if (sum == 0) {
return new Node(createFraction(bound), null, null, 1);
}
ThreadLocalRandom random = ThreadLocalRandom.current();
//1.否则就是构造符号节点
final SymbolNode parent = new SymbolNode(null, null, SYMBOLS[random.nextInt(4)]);
int left = random.nextInt(sum);
//2.递归下去构造左孩子和右孩子
parent.left = build(left);
parent.right = build(sum - left - 1);
//3.然后计算结果
Fraction result = calculate(parent.symbol, parent.left.result, parent.right.result);
//4.如果是负数就取绝对值,然后交换左右孩子
if (result.isNegative()) {
Node tmp = parent.left;
parent.left = parent.right;
parent.right = tmp;
result.abs();
}
parent.result = result;
//5.计算树高
parent.high = Math.max(parent.left.high, parent.right.high) + 1;
return parent;
} /** 根据 string 表达式构建树
* @param expression 表达式
* @return node
*/
private Node build(String expression) {
String[] strings = expression.split(" ");
Stack功能:Function
/**
* @param sum 符号数量
* @param bound 范围
*/
public void outputExercises(int sum, int bound) {
if (bound set = new HashSet();
try (BufferedWriter exercisesWriter = new BufferedWriter(new FileWriter("Exercises.txt"));
BufferedWriter answerWriter = new BufferedWriter(new FileWriter("Answers.txt"))
) {
for (int i = 1; set.size() /**
* 输出结果
* @param exercisePath 表达式文件路径
* @param answerPath 结果文件路径
* @param gradePath 输出结果文件路径
*/
public void outputGrade(String exercisePath, String answerPath, String gradePath) {
try (BufferedReader exReader = new BufferedReader(new FileReader(exercisePath));
BufferedReader anReader = new BufferedReader(new FileReader(answerPath));
BufferedWriter gradeWriter = new BufferedWriter(new FileWriter(gradePath))
) {
String ex, an;
int c = 0, w = 0;
StringBuilder correct = new StringBuilder("Correct: %d (");
StringBuilder wrong = new StringBuilder("Wrong: %d (");
while ((ex = exReader.readLine()) != null && (an = anReader.readLine()) != null) {
int exPoint = ex.indexOf(".");
int anPoint = an.indexOf(".");
if (exPoint != -1 && anPoint != -1) {
int i = Integer.valueOf(ex.substring(0,exPoint).trim());
Expression expression = new Expression(ex.substring(exPoint + 1));
Fraction answer = new Fraction(an.substring(anPoint + 1));
if (expression.getResult().equals(answer.toString())) {
c++;
correct.append(" ").append(i);
if (c % 20 == 0) {
correct.append("\n");
}
} else {
w++;
wrong.append(" ").append(i);
if (w % 20 == 0) {
wrong.append("\n");
}
}
}
}
gradeWriter.write(String.format(correct.append(" )\n").toString(),c));
gradeWriter.write(String.format(wrong.append(" )\n").toString(),w));
gradeWriter.flush();
} catch (IOException e) {
e.printStackTrace();
}
}测试
表达式的输出
private Function function = new Function();
@Test
public void outputExercises() {
function.outputExercises(10,20);
}1.2‘13/17 × ( 10 + 11 )
2.16 - 6
3.( 8 - 1‘5/9 ) ÷ ( 16 ÷ 5‘9/17 )
4.1‘5/14 ÷ ( 1/6 × 3 )
5.4‘1/9 ÷ 15
6.11 - 6/19 - 4‘1/3 ÷ 1
7.9 - 4
8.1 ÷ ( ( 8/19 - 0 ) ÷ 2 )
9.12 - 9 ÷ ( 1‘1/15 + 5 )
10.9 ÷ ( 15 - 9 - 11/15 )1.58‘1/17
2.10
3.2‘139/612
4.2‘5/7
5.37/135
6.6‘20/57
7.5
8.4‘3/4
9.10‘47/91
10.1‘56/79结果的对比
private Function function = new Function();
@Test
public void outputGrade() {
function.outputGrade("Exercises.txt","Answers.txt","Grade.txt");
}Correct: 10 ( 1 2 3 4 5 6 7 8 9 10 )
Wrong: 0 ( )Correct: 8 ( 1 3 4 5 6 8 9 10 )
Wrong: 2 ( 2 7 )PSP
PSP2.1
Personal Software Process Stages
预估耗时(分钟)
实际耗时(分钟)
Planning
计划
30
60
· Estimate
· 估计这个任务需要多少时间
30
60
Development
开发
870
1415
· Analysis
· 需求分析 (包括学习新技术)
30
60
· Design Spec
· 生成设计文档
30
150
· Design Review
· 设计复审 (和同事审核设计文档)
120
120
· Coding Standard
· 代码规范 (为目前的开发制定合适的规范)
30
20
· Design
· 具体设计
30
120
· Coding
· 具体编码
360
1200
· Code Review
· 代码复审
30
45
· Test
· 测试(自我测试,修改代码,提交修改)
240
300
Reporting
报告
80
80
· Test Report
· 测试报告
20
40
· Size Measurement
· 计算工作量
30
20
· Postmortem & Process Improvement Plan
· 事后总结, 并提出过程改进计划
30
20
合计
980
2155
总结