树状数组浅讲
2021-07-11 09:07
标签:规律 遍历 src get span 前缀 png 维护 images rt,个人肤浅理解,各位神犇请自动出门右转 不同于传统数组每个元素单独存放,求和时遍历相加,树状数组每个元素不单独维护,而是被维护在一个包含其他元素的前缀和里。宜先仔细揣摩后再行。 上图便体现了树状数组储存数据的原理 相当于以下等式 说明:C[]是树状数组,A[]是实际元素 C[1]=A[1]; C[2]=A[1]+A[2]; C[3]=A[3]; C[4]=A[1]+A[2]+A[3]+A[4]; C[5]=A[5]; C[6]=A[5]+A[6]; C[7]=A[7]; C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]; 如此存储,便可以体现出上面所说每个元素不单独维护,而是被维护在一个包含其他元素的前缀和里的维护原则,比如元素1(即\(A[1]\))便包含在C[1],C[2],C[4],C[8]中,而如今有一个神器 lowbit(1)=1 lowbit(2)=2 lowbit(3)=1 lowbit(4)=4 lowbit(5)=1 lowbit(6)=2 lowbit(7)=1 lowbit(8)=8 这时你会发现一个规律:每次当前下标再加上当前下标的lowbit值便会得到下一个包含元素i的\(C[k]\)的下标,比如第一个包含元素1的\(C[k]\)为\(C[1]\),那么下一个(第二个)包含元素1的\(C[k]\)为\(C[1+lowbit(1)]\),如此按照此规律循环便可访问到所有包含元素i的\(C[k]\)们 于是下面遍历所有包含元素i的\(C[k]\)的程序成立 于是你又可以在遍历的同时顺便修改一下值(又于是下面修改元素i的值的程序成立) 同理,你又会发现其实查询前缀和的规律也是如此,读者可以动手模拟一下 于是查询前缀和的程序又成立 完整的树状数组板子 以上。 树状数组浅讲 标签:规律 遍历 src get span 前缀 png 维护 images 原文地址:https://www.cnblogs.com/santiego/p/9551655.html树状数组浅讲
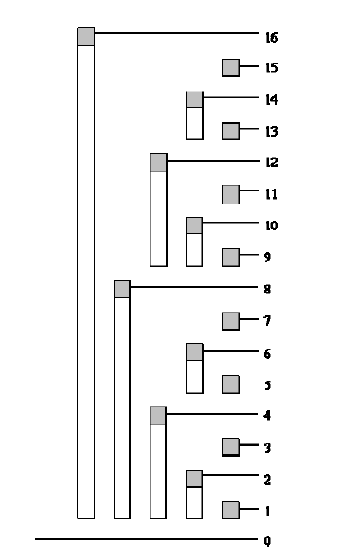
lowbit(x)=x&(-x)可以依次推出所有包含元素i的\(C[k]\)们,我们先看看1至8的lowbit值void spot(int x)
{
for(int i=x;ivoid add(int x, int v)
{
for(int i=x;iint getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=tree[i];
return ans;
}int lowbit(int x){return x&(-x);}
void add(int x, int v)
{
for(int i=x;i0;i-=lowbit(i))
ans+=tree[i];
return ans;
}