浅谈字符串算法(KMP算法和Manacher算法)
2021-07-12 13:08
标签:range 效率 res i++ 超过 lan color sub 扩展 Subtask1(10pts):最朴素的暴力 枚举字符串的所有子串,判断其是否回文,时间复杂度是O(n3)的 Subtask2(30pts):利用回文串的性质: 所有的回文串都是对称的。 长度为奇数回文串以最中间字符的位置为对称轴左右对称, 而长度为偶数的回文串的对称轴在中间两个字符之间的空隙。 可以遍历这些对称轴, 在每个对称轴上同时向左和向右扩展,直到左右两边的字符不同或者到达边界。 时间复杂度O(n2) Subtask3(100pts):?(当然是Manacher算法囖)O(n) 改进优化 Subtask2(30pts) : 1.麻烦程度(预处理字符串) 在每两个字符中间插入另一个字符,如‘#‘。 也就是说,原来的字符串是这样的 现在的字符串是这样的(为了不越界以及方便,a[0]设置为‘#’) 那么这个缺点解决了(现在不用分奇数偶数讨论了qwq) 【图是哪里偷过来的,足以说明问题】 2.会出现很多子串被重复多次访问,时间效率大幅降低。 要想降维 O(n)的做法是每一位只扫一次或常数次这里每一位都扫了将近n次 ------------------(正文分割线)---------------------- 定义几个变量P[i]表示在处理过后的数组中的第i个点最长向左边拓展P[i]个数位都能保证他是回文(右边不记录因为左右对称) 那么p[1]=1,p[2]=2,p[3]=1,p[4]=2,p[5]=1,p[6]=2,p[7]=5,p[8]=2,p[9]=1,p[10]=2,p[11]=1,p[12]=2,p[13]=1; 可以发现所有#的地方大部分都是1 其实上面那句话是错的!!! p[7]=5 ??? P[i]-1代表什么? 原串(不插入#前)中第i位置的回文串长度(包含中间点) 证明: 1、显然L=2*P[i]-1即为新串(加#)中以第i个点为中心最长回文串长度。 得证。 【再偷2张图片】 maxId表示前面运行过程中求得最大回文串的最右端 id(后面程序是MID)表示此时最大回文串的对称点,i代表当前遍历到第i个位置 显然我们可以轻易算出i关于id(MID)对称点的坐标j 由id是ij的中点可知 (i+j)/2=id,由此可知 j=2*id-i(所以程序运行的时候就不用记录j了直接用id和i算就行) 运用动态规划的思想在算P[i]的时候P[j] | j∈ [1,i) 都已经算出那么若j为i关于id(MID)的对称点那么P[i]∈ [P[j],+∞) 就是P[i]不可能比P[j]短,为什么呢? 利用回文串的对称性j和i关于id(MID)对称,MaxId和左边MinId(对于id(MID)的对称点)关于id对称 那么j到id回文串半径为P[j],对称过来到id右边i的左边那么回文串半径也为P[j], 而P[i]没有算出来所以就是P[i]不可能比P[j]短 即 P[i]∈ [P[j],+∞) 分类讨论: 若对称过来超过MaxId那么这样的对称是不合法的 P[j]=1从该点老老实实向两边拓展 就是P[j]对称到i的左右,i右端超过MaxId(触及不该触及的地方),就是不合法,因为右边你并不知道 若对称过来没有超过MaxId那么这样的对称是合法的 P[i]=p[j]然后往右拓展 在移动的过程中顺便更新MaxId和P[i]就行 到这里你已经完成了 Subtask3 对于100%的数据|S|
复杂度证明? manacher算法只需要线性扫描一遍预处理后的字符串。 1. (i 2.其他情况 p[i]=0 1. 在i 但是在情况2下,每次扫描都从MaxId开始,且MaxId自身的变化情况是单调递增的, 这样可以保证,字符串中的每个字符最多被访问2次, 所以,该算法的时间复杂度是线性O(n) 只需要弄清楚两点: 1.while()循环本身的时间复杂度在没有前提条件的情况下确实是O(n) 2.但是这里的MaxId,是不断往后走而不可能往前退的,它自身的值的变化是递增的。 那么你可以明白,要进入while循环, i 的值必然是比MaxId大的, 也就是说整个程序结束为止, while循环执行的操作数为n次(线性次), 而字符串中的每个字符,最多能被访问到2次。 时间复杂度必然为O(n) 贴下代码: 给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度. 字符串长度为n 输入格式: 一行小写英文字符a,b,c...y,z组成的字符串S 输出格式: 一个整数表示答案 字符串长度|S|
这里有着注意点:不能判断回车否则是TLE,应该判断不是字母时果断跳出 浅谈字符串算法(KMP算法和Manacher算法) 标签:range 效率 res i++ 超过 lan color sub 扩展 原文地址:https://www.cnblogs.com/ljc20020730/p/9546690.html【字符串算法1】 字符串Hash(优雅的暴力)
【字符串算法2】Manacher算法
【字符串算法3】KMP算法
这里将讲述 字符串算法2:Manacher算法
问题:给出字符串S(限制见后)求出最大回文子串长度
Subtask1 对于10%的数据 |S|∈(0,100]
Subtask2 对于30%的数据|S|∈(0,5000]
Subtask3 对于100%的数据|S|∈(0,11000000]

重点来了:
2、以第i位 为中心的回文串一定是以#开头和#结尾的,例如“#b#b#”或“#b#a#b#”
所以L减去最前或者最后的‘#’字符就是原串中长度的二倍,即原串长度为(L-1)/2,化简的P[i]-1。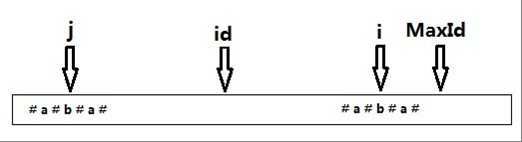
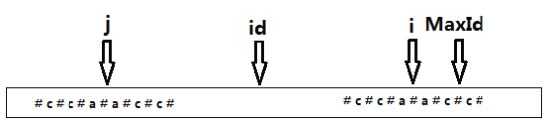
对p[]数组的处理 i 为 j 关于 id 的对称点
# include
这是一道真正的模板题qwq:
P3805 【模板】manacher算法
题目描述
输入输出格式
输入输出样例
aaa
3
说明
上一篇:hive排序
文章标题:浅谈字符串算法(KMP算法和Manacher算法)
文章链接:http://soscw.com/index.php/essay/104173.html