基于MATLAB的腐蚀膨胀算法实现
2021-07-15 16:05
标签:view 简单 扩大 tps ble .com 分离 填充物 开源 本篇文章要分享的是基于MATLAB的腐蚀膨胀算法实现,腐蚀膨胀是形态学图像处理的基础,腐蚀在二值图像的基础上做“收缩”或“细化”操作,膨胀在二值图像的基础上做“加长”或“变粗”的操作。 什么是二值图像呢?把一幅图片看做成一个二维的数组,那么二值图像是一个只有0和1的逻辑数组,我们前面Sobel边缘检测后的图像输出边缘效果,设置个阈值,大于阈值输出为1,小于阈值输出为0,最后输出就是一幅二维图像了。 腐蚀是一种消除边界点,使边界向内部收缩的过程。可以用来消除小且无意义的物体。用3X3的结构元素,扫描图像的每一个像素,用结构元素与其覆盖的二值图像做“与”操作,如果都为1,结果图像的该像素为1。否则为0。结果会使二值图像小一圈。 有一个形象的比喻来可以说明该运算,用0表示蛀虫,1表示大米。蛀虫腐蚀大米的过程便是腐蚀运算, 腐蚀 如图所示,对于一个像素矩阵而言,只要有蛀虫(0)的存在,大米(1)就会被腐蚀掉了,即使只存在一个蛀虫(0),但是还是会被蛀虫腐蚀完毕,最后一幅图上面由于没有蛀虫(0)所以大米完好无损。 关于算法的实现,可以用下式子来表示,即3x3像素的运算: P = P11 & P12 & P13 & P21 & P22 & P23 & P31 & P32 & P33 在FPGA中,为了通过面积去换速度,我们将上式改变如下: P1 = P11 & P12 & P13 P2 = P21 & P22 & P23 P3 = P31 & P32 & P33 P = P1 & P2 & P3 MATLAB中可以直接写一个按位或运算。 膨胀是将与物体接触的所有背景点合并到该物体中,使边界向外部扩张的过程。可以用来填补物体中的空洞。用3X3的结构元素,扫描图像的每一个像素,用结构元素与其覆盖的二值图像做“与”操作,如果都为0,结果图像的该像素为0,。否则为1。结果使二值图像扩大一圈。 先腐蚀后膨胀的过程称为开运算。用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显的改变其面积。先膨胀后腐蚀的过程称为比运算,用来填充物体内细小空间、连接邻近物体、平滑其边界的同时并不明显改变其面积。 膨胀算法用最简单的比喻来描述:0表示害虫,1表示青蛙,青蛙吃了害虫表示膨胀运算,我们用3*3像素阵列来解释: 膨胀 如图所示,图左只有害虫(0),所以害虫都活着,中间那个图,虽然只有一个害虫,但是还是会被青蛙全部吃掉,最右边的那幅图,都是青蛙,所以青蛙始终是青蛙。 关于算法的实现,可以用下式子来表示,即3x3像素的运算: P = P11 | P12 | P13 | P21 | P22 | P23 | P31 | P32 | P33 在HDL中,为了通过面积去换速度,我们将上式改变如下: P1 = P11 | P12 | P13 P2 = P21 | P22 | P23 P3 = P31 | P32 | P33 P = P1 | P2 | P3 MATLAB中可以直接写一个按位与运算。 先腐蚀后膨胀叫开运算,开运算的作用是清除图像边缘周围非边缘的细小的点。先膨胀后腐蚀为闭运算,闭运算的作用是清除图像内部的空洞, 如果我们的目标物体外面有很多无关的小区域,就用开运算去除掉;如果物体内部有很多小黑洞,就用闭运算填充掉。 bitand(), 对十进制数进行逐位逻辑与运算:先将十进制数转换成二进制数,然后逐位与运算,其运算结果转换为十进制。 bitor(), 对十进制数进行逐位逻辑或运算:先将十进制数转换成二进制数,然后逐位与运算,其运算结果转换为十进制。 为了可以清晰的看到图像边缘的变化,我们把黑色作为背景,白色作为边缘。 Sobel边缘检测后的lena 腐蚀后的lena 膨胀后的lena 先腐蚀后膨胀开运算lena 先膨胀后腐蚀闭运算lena 从上面两幅图可以看出,腐蚀后的图像边缘明显变细,消除了更多假边缘,在腐蚀基础上使用膨胀算法的lena将腐蚀后的边缘扩大、加粗,这样看起来更清楚。 转载请注明出处:NingHeChuan(宁河川) 个人微信订阅号:开源FPGA 如果你想及时收到个人撰写的博文推送,可以扫描左边二维码(或者长按识别二维码)关注个人微信订阅号 知乎ID:NingHeChuan 微博ID:NingHeChuan 原文地址:https://www.cnblogs.com/ninghechuan/p/9527915.html 基于MATLAB的腐蚀膨胀算法实现 标签:view 简单 扩大 tps ble .com 分离 填充物 开源 原文地址:https://www.cnblogs.com/ninghechuan/p/9530964.html腐蚀
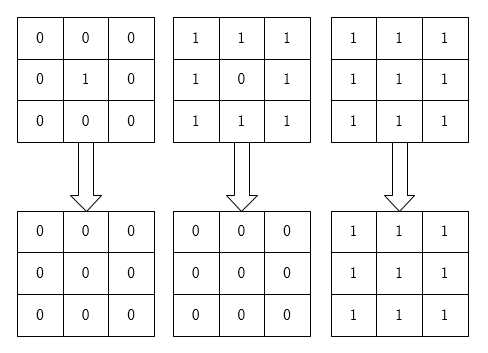
膨胀
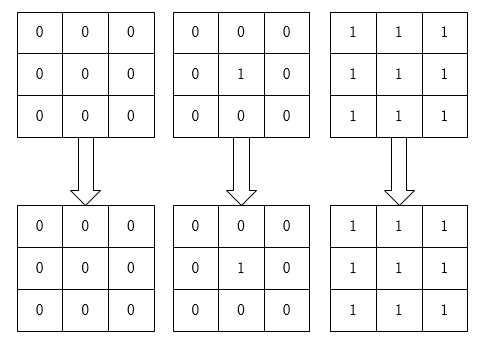
开运算闭运算
MATLAB逻辑运算函数
MATLAB代码实现
1 %RGB_YCbCr
2 clc;
3 clear all;
4 close all;
5
6 RGB_data = imread(‘lena.jpg‘);
7
8 R_data = RGB_data(:,:,1);
9 G_data = RGB_data(:,:,2);
10 B_data = RGB_data(:,:,3);
11
12 %imshow(RGB_data);
13
14 [ROW,COL, DIM] = size(RGB_data);
15
16 Y_data = zeros(ROW,COL);
17 Cb_data = zeros(ROW,COL);
18 Cr_data = zeros(ROW,COL);
19 Gray_data = RGB_data;
20
21 for r = 1:ROW
22 for c = 1:COL
23 Y_data(r, c) = 0.299*R_data(r, c) + 0.587*G_data(r, c) + 0.114*B_data(r, c);
24 Cb_data(r, c) = -0.172*R_data(r, c) - 0.339*G_data(r, c) + 0.511*B_data(r, c) + 128;
25 Cr_data(r, c) = 0.511*R_data(r, c) - 0.428*G_data(r, c) - 0.083*B_data(r, c) + 128;
26 end
27 end
28
29 Gray_data(:,:,1)=Y_data;
30 Gray_data(:,:,2)=Y_data;
31 Gray_data(:,:,3)=Y_data;
32
33 figure;
34 imshow(Gray_data);
35
36 %Median Filter
37 imgn = imnoise(Gray_data,‘salt & pepper‘,0.02);
38
39 figure;
40 imshow(imgn);
41
42 Median_Img = Gray_data;
43 for r = 2:ROW-1
44 for c = 2:COL-1
45 median3x3 =[imgn(r-1,c-1) imgn(r-1,c) imgn(r-1,c+1)
46 imgn(r,c-1) imgn(r,c) imgn(r,c+1)
47 imgn(r+1,c-1) imgn(r+1,c) imgn(r+1,c+1)];
48 sort1 = sort(median3x3, 2, ‘descend‘);
49 sort2 = sort([sort1(1), sort1(4), sort1(7)], ‘descend‘);
50 sort3 = sort([sort1(2), sort1(5), sort1(8)], ‘descend‘);
51 sort4 = sort([sort1(3), sort1(6), sort1(9)], ‘descend‘);
52 mid_num = sort([sort2(3), sort3(2), sort4(1)], ‘descend‘);
53 Median_Img(r,c) = mid_num(2);
54 end
55 end
56
57 figure;
58 imshow(Median_Img);
59
60 %Sobel_Edge_Detect
61
62 Median_Img = double(Median_Img);
63 Sobel_Threshold = 150;
64 Sobel_Img = zeros(ROW,COL);
65
66 for r = 2:ROW-1
67 for c = 2:COL-1
68 Sobel_x = Median_Img(r-1,c+1) + 2*Median_Img(r,c+1) + Median_Img(r+1,c+1) - Median_Img(r-1,c-1) - 2*Median_Img(r,c-1) - Median_Img(r+1,c-1);
69 Sobel_y = Median_Img(r-1,c-1) + 2*Median_Img(r-1,c) + Median_Img(r-1,c+1) - Median_Img(r+1,c-1) - 2*Median_Img(r+1,c) - Median_Img(r+1,c+1);
70 Sobel_Num = abs(Sobel_x) + abs(Sobel_y);
71 %Sobel_Num = sqrt(Sobel_x^2 + Sobel_y^2);
72 if(Sobel_Num > Sobel_Threshold)
73 Sobel_Img(r,c)=255;
74 else
75 Sobel_Img(r,c)=0;
76 end
77 end
78 end
79
80 figure;
81 imshow(Sobel_Img);
82
83 %imopen Erosion_Dilation
84 %Erosion
85 % Erosion_img = zeros(ROW,COL);
86 % for r = 2:ROW-1
87 % for c = 2:COL-1
88 % and1 = bitand(Sobel_Img(r-1, c-1), bitand(Sobel_Img(r-1, c), Sobel_Img(r-1, c+1)));
89 % and2 = bitand(Sobel_Img(r, c-1), bitand(Sobel_Img(r, c), Sobel_Img(r, c+1)));
90 % and3 = bitand(Sobel_Img(r+1, c-1), bitand(Sobel_Img(r+1, c), Sobel_Img(r+1, c+1)));
91 % Erosion_img(r, c) = bitand(and1, bitand(and2, and3));
92 % end
93 % end
94
95 % figure;
96 % imshow(Erosion_img);
97
98 % %Dilation
99 % Dilation_img = zeros(ROW,COL);
100 % for r = 2:ROW-1
101 % for c = 2:COL-1
102 % or1 = bitor(Erosion_img(r-1, c-1), bitor(Erosion_img(r-1, c), Erosion_img(r-1, c+1)));
103 % or2 = bitor(Erosion_img(r, c-1), bitor(Erosion_img(r, c), Erosion_img(r, c+1)));
104 % or3 = bitor(Erosion_img(r+1, c-1), bitor(Erosion_img(r+1, c), Erosion_img(r+1, c+1)));
105 % Dilation_img(r, c) = bitor(or1, bitor(or2, or3));
106 % end
107 % end
108
109 % figure;
110 % imshow(Dilation_img);
111
112 %imclose Erosion_Dilation
113 %Dilation
114 Dilation_img = zeros(ROW,COL);
115 for r = 2:ROW-1
116 for c = 2:COL-1
117 or1 = bitor(Sobel_Img(r-1, c-1), bitor(Sobel_Img(r-1, c), Sobel_Img(r-1, c+1)));
118 or2 = bitor(Sobel_Img(r, c-1), bitor(Sobel_Img(r, c), Sobel_Img(r, c+1)));
119 or3 = bitor(Sobel_Img(r+1, c-1), bitor(Sobel_Img(r+1, c), Sobel_Img(r+1, c+1)));
120 Dilation_img(r, c) = bitor(or1, bitor(or2, or3));
121 end
122 end
123
124 figure;
125 imshow(Dilation_img);
126
127 %Erosion
128 Erosion_img = zeros(ROW,COL);
129 for r = 2:ROW-1
130 for c = 2:COL-1
131 and1 = bitand(Dilation_img(r-1, c-1), bitand(Dilation_img(r-1, c), Dilation_img(r-1, c+1)));
132 and2 = bitand(Dilation_img(r, c-1), bitand(Dilation_img(r, c), Dilation_img(r, c+1)));
133 and3 = bitand(Dilation_img(r+1, c-1), bitand(Dilation_img(r+1, c), Dilation_img(r+1, c+1)));
134 Erosion_img(r, c) = bitand(and1, bitand(and2, and3));
135 end
136 end
137
138 figure;
139 imshow(Erosion_img);
处理后结果对比






下一篇:Java基础_JDK5常用特性
文章标题:基于MATLAB的腐蚀膨胀算法实现
文章链接:http://soscw.com/index.php/essay/105636.html