【优化算法】动态粒子群算法的动态环境寻优算法【含Matlab源码 1125期】
2021-07-25 18:55
标签:有一个 速度 最简 就是 优化问题 end 位置 改变 迭代 粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。CAS理论于1994年正式提出,CAS中的成员称为主体。比如研究鸟群系统,每个鸟在这个系统中就称为主体。主体有适应性,它能够与环境及其他的主体进行交流,并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括:新层次的产生(小鸟的出生);分化和多样性的出现(鸟群中的鸟分成许多小的群);新的主题的出现(鸟寻找食物过程中,不断发现新的食物)。 版本:2014a 【优化算法】动态粒子群算法的动态环境寻优算法【含Matlab源码 1125期】 标签:有一个 速度 最简 就是 优化问题 end 位置 改变 迭代 原文地址:https://www.cnblogs.com/homeofmatlab/p/14994824.html一、简介
所以CAS系统中的主体具有4个基本特点(这些特点是粒子群算法发展变化的依据):
首先,主体是主动的、活动的。
主体与环境及其他主体是相互影响、相互作用的,这种影响是系统发展变化的主要动力。
环境的影响是宏观的,主体之间的影响是微观的,宏观与微观要有机结合。
最后,整个系统可能还要受一些随机因素的影响。
粒子群算法就是对一个CAS系统---鸟群社会系统的研究得出的。
粒子群算法( Particle Swarm Optimization, PSO)最早是由Eberhart和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。在PSO中,每个优化问题的潜在解都可以想象成d维搜索空间上的一个点,我们称之为“粒子”(Particle),所有的粒子都有一个被目标函数决定的适应值(Fitness Value ),每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索。Reynolds对鸟群飞行的研究发现。鸟仅仅是追踪它有限数量的邻居但最终的整体结果是整个鸟群好像在一个中心的控制之下.即复杂的全局行为是由简单规则的相互作用引起的。二、源代码
%% 动态粒子群算法
%% 清空环境
clear
clc
%% 设置双峰参数
% 设置con1参数
X1 = 25;
Y1 = 25;
H1 =410;
%设置con2参数
H2=zeros(1,1200);
i=1:200;
H2(i)=450-fix(i/5);
i=201:700;
H2(i)=410;
i=701:1000;
H2(i)=350 + fix((i-500)/10)*3;
i=1001:1200;
H2(i) = 500;
X2=zeros(1,1200);
i=1:1200;
Y2(i)=-25;
i=1:500;
X2(i)=-25 + (i-1)*25/500;
i=501:1000;
X2(i)=0;
i=1001:1200;
X2(i)=(i-1000)*25/200;
%% 初始化粒子和敏感粒子
% 种群规模
n = 20;
% 粒子和敏感粒子
pop = unidrnd(501,[n,2]);
popTest = unidrnd(501,[5*n,2]);
% 数字高度
h = DF1function(X1,Y1,H1,X2(1),Y2(1),H2(1));
V = unidrnd(100,[n,2])-50;
Vmax=25;Vmin=-25;
%% 粒子和敏感粒子适应度值
fitness=zeros(1,n);
fitnessTest=zeros(1,n);
for i=1:n
fitness(i)=h(pop(i,1),pop(i,2));
fitnessTest(i)=h(popTest(i,1),popTest(i,2));
end
oFitness=sum(fitnessTest); %敏感粒子
[value,index]=max(fitness);
popgbest=pop;
popzbest=pop(index,:);
fitnessgbest=fitness;
fitnesszbest=fitness(index);
%% 算法参数
vmax = 10;
vmin = -10;
popMax=501;
popMin=1;
m = 2;
nFitness = oFitness;
Tmax=100; %每次迭代次数
fitnessRecord=zeros(1,1200);
%% 循环寻找最优点
for k = 1:1200
k
% 新数字地图
h = DF1function(X1,Y1,H1,X2(k),Y2(k),H2(k));
% 敏感粒子变化
for i=1:5*n
fitnessTest(i)=h(popTest(i,1),popTest(i,2));
end
oFitness=sum(fitnessTest);
% 变化超过阈值,重新初始化
if abs(oFitness - nFitness)>1
index=randperm(20);
pop(index(1:10),:)=unidrnd(501,[10,2]);
V(index(1:10),:)=unidrnd(100,[10,2])-50;
end
% 粒子搜索
for i=1:Tmax
for j=1:n
% 速度更新
V(j,:)=V(j,:)+floor(rand*(popgbest(j,:)-pop(j,:)))+floor(rand*(popzbest - pop(j,:)));
index1=find(V(j,:)>Vmax);
V(j,index1)=Vmax;
index2=find(V(j,:)三、运行结果
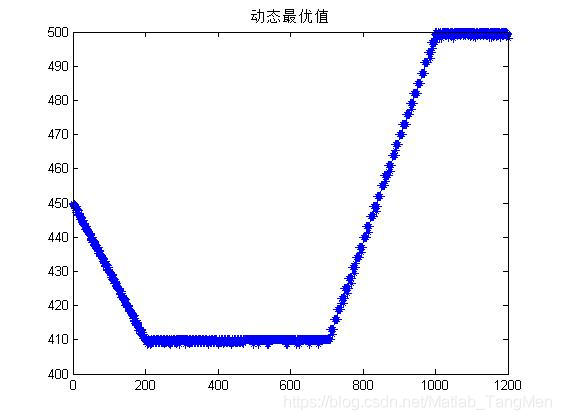
四、备注
文章标题:【优化算法】动态粒子群算法的动态环境寻优算法【含Matlab源码 1125期】
文章链接:http://soscw.com/index.php/essay/106959.html