时序图与状态图（Rose） - Windows XP经典软件系列

标签：avl树   平衡二叉查找树   

         最近开始了自己高级数据结构之旅，在这次旅行中，我将持续把一些高级的数据结构从理论到编码都过一遍，同时通过博客形式分享出来，希望大家指出不足之处！
     二叉排序树是一种动态排序的数据结构，支持插入、删除、查找等操作，且平均时间复杂度为O(log(N))，但是普通二叉排序树不能保证树退化为一颗分支的情况，此时最坏情况下的时间复杂度为O（N）。此时，平衡二叉树的产生了。平衡二叉树是一种动态调整平衡的数据结构，但理想的平衡二叉树很难，于是人们使用AVL、红黑树、Treap、伸展树等来替代平衡二叉树，这些数据结构可以很好地改善最坏情况。但实现起来并不是很容易的事。

      AVL树是一种高度平衡的二叉查找树，但不是严格意义上的平衡二叉查找树。但AVL树实现相对简单，这里指相对简单。查找、插入、删除、修改等基本操作时间复杂度均为O(log(N))，此处指所有情况下（包括平均、最好、最坏）。一般情况下AVL树要维护一个平衡因子，但在实现时可以直接用高度避免节点所占空间变大。

调整

          主要有两种操作，左旋LeftRotate、右旋RightRotate，在此基础上衍生出先左后右旋转LeftAndRightRotate，先右后左旋转RightAndLeftRotate。具体要视情况调整，下面是说明每种情况使用的场合。

（1）、左旋LeftRotate：2==当前节点右子树高度-当前节点左子树高度，并且右子树的右孩子节点高度大于右子树的左孩子节点高度，直接左旋。如图所示：

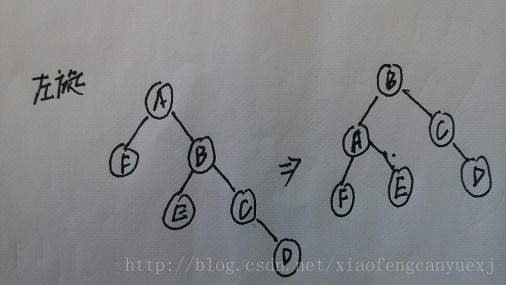
（2）、右旋RightRotate：-2==当前节点右子树高度-当前节点左子树高度，并且左子树的左孩子节点高度大于左子树的右孩子节点高度，直接左旋。如图所示：

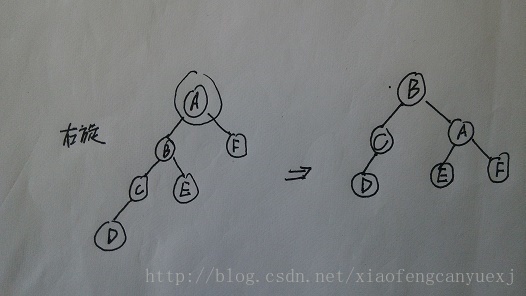
（3）、先左后右旋转LeftAndRightRotate：-2==当前节点右子树高度-当前节点左子树高度，并且左子树的左孩子节点高度小于左子树的右孩子节点高度，直接左旋。如图所示：

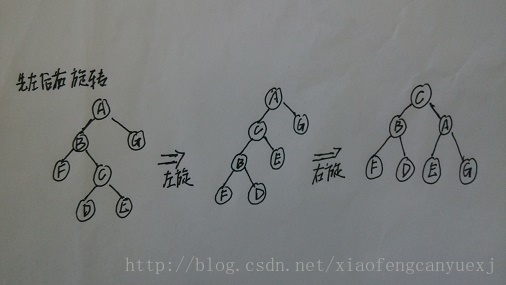
（4）、先右后左旋转RightAndLeftRotate：2==当前节点右子树高度-当前节点左子树高度，并且右子树的右孩子节点高度小于右子树的左孩子节点高度，直接左旋。如图所示：

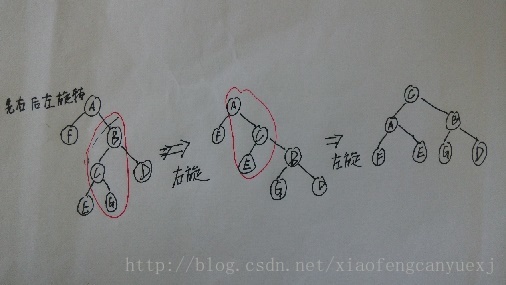
插入

      在插入一个元素以后，很有可能不再平衡，此时需要调整平衡。可以从不在平衡的最底层节点开始，依据调整规则旋转，然后一次上调，这样最终就能保证处于平衡状态。此过程时间复杂度为O(log(N))，不将会出现极端情况。由于之前是平衡的，所以不平衡因素必定在根节点到当前插入节点的路径上，故只需调整此路径即可。

删除

     要删除一个元素，可能有两种情况需要考虑，如下：

    A、如果该元素所在节点没有右孩子节点，直接删除；

    B、如果有右孩子，需找到右孩子所在子树的最大元素，用其替代本应删除节点元素，剩下就转到删除该右子树最小元素节点。当然可以找到左子树最大元素节点替代，只是1中条件也应相应的改变。

     在删除一个元素后，很有可能不再平衡，此时需要调整平衡。可以从不在平衡的最底层节点开始，依据调整规则旋转，然后一次上调，这样最终就能保证处于平衡状态。此过程时间复杂度为O(log(N))，不将会出现极端情况。由于之前是平衡的，所以不平衡因素必定在根节点到当前插入节点的路径上，故只需调整此路径即可。

修改

     修改在前面已有插入、删除的基础上就相对简单了，只需首先删除旧元素，然后插入新元素，时间复杂度为O(log(N))。由于转换成了先删除后插入的操作，所以能保证平衡。

源程序代码

//AVLTreeNode.h头文件，定义节点信息
#include
using namespace std;

/**********************************
*功能:防止头文件多次包含
**********************************/
#ifndef AVLTREENODE_H
#define AVLTREENODE_H


struct AVLTreeNode
{
	int key;
	int height;
	AVLTreeNode *leftChild;
	AVLTreeNode *rightChild;
	AVLTreeNode(int tempKey)
	{
		height=0;
		key=tempKey;
		leftChild=NULL;
		rightChild=NULL;
	}
};

#endif AVLTREENODE_H

//AVLTree.cpp源文件，完成AVL树的基本操作
#include
#include
#include"AVLTreeNode.h"
using namespace std;

class AVLTree
{
private:
	AVLTreeNode *root;
	AVLTreeNode *Search(int,AVLTreeNode *);
	AVLTreeNode *LeftRotate(AVLTreeNode *);
	AVLTreeNode *LeftAndRightRotate(AVLTreeNode *);
	AVLTreeNode *RightRotate(AVLTreeNode *);
	AVLTreeNode *RightAndLeftRotate(AVLTreeNode *);
	int GetHeight(AVLTreeNode *);
	void PreOrderPrint(AVLTreeNode *);
	void InOrderPrint(AVLTreeNode *);
	void SufOrderPrint(AVLTreeNode *);
	void RotatePrint(AVLTreeNode *,int);
	AVLTreeNode *Insert(int,AVLTreeNode *);
	AVLTreeNode *Delete(bool&,int,AVLTreeNode *);
public:
	AVLTree();
	void Insert(int);
	bool Search(int);
	bool Delete(int);
	bool Updata(int,int);
	void PreOrderPrint();
	void InOrderPrint();
	void SufOrderPrint();
	void RotatePrint();
};


AVLTree::AVLTree()
{
	root=NULL;
}

/*********************************************
*参数：当前节点
*返回值：当前节点高度
*功能：返回当前节点高度
**********************************************/
int AVLTree::GetHeight(AVLTreeNode *tempNode)
{
	return NULL==tempNode?-1:tempNode->height;
}

/*********************************************
*参数：待查找元素，当前节点
*返回值：元素所在节点
*功能：返回元素所在节点
**********************************************/
AVLTreeNode *AVLTree::Search(int tempKey,AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return NULL;
	else if(tempKey==tempNode->key)
		return tempNode;
	else if(tempKeykey)
		return Search(tempKey,tempNode->leftChild);
	return Search(tempKey,tempNode->rightChild);
}
bool AVLTree::Search(int tempKey)
{
	if(NULL==Search(tempKey,root))
		return false;
	return true;
}

/*********************************************
*参数：当前节点
*返回值：当前子树根节点
*功能：左旋调平衡
**********************************************/
AVLTreeNode *AVLTree::LeftRotate(AVLTreeNode *tempNode)
{
	AVLTreeNode *lChildNode=tempNode->rightChild->leftChild,*newRoot=tempNode->rightChild;
	tempNode->rightChild->leftChild=tempNode;
	tempNode->rightChild=lChildNode;
	tempNode->height=max(GetHeight(tempNode->leftChild),GetHeight(tempNode->rightChild))+1;
	if(NULL!=tempNode->rightChild)
		tempNode->rightChild->height=max(GetHeight(tempNode->rightChild->leftChild),GetHeight(tempNode->rightChild->rightChild))+1;
	return newRoot;
}

/*********************************************
*参数：当前节点
*返回值：当前子树根节点
*功能：右旋调平衡
**********************************************/
AVLTreeNode *AVLTree::RightRotate(AVLTreeNode *tempNode)
{
	AVLTreeNode *rChildNode=tempNode->leftChild->rightChild,*newRoot=tempNode->leftChild;
	tempNode->leftChild->rightChild=tempNode;
	tempNode->leftChild=rChildNode;
	tempNode->height=max(GetHeight(tempNode->leftChild),GetHeight(tempNode->rightChild))+1;
	if(NULL!=tempNode->leftChild)
		tempNode->leftChild->height=max(GetHeight(tempNode->leftChild->leftChild),GetHeight(tempNode->leftChild->rightChild))+1;
	return newRoot;
}

/*********************************************
*参数：当前节点
*返回值：当前子树根节点
*功能：先左旋后右旋调平衡
**********************************************/
AVLTreeNode *AVLTree::LeftAndRightRotate(AVLTreeNode *tempNode)
{
	tempNode->leftChild=LeftRotate(tempNode->leftChild);
	return RightRotate(tempNode);
}

/*********************************************
*参数：当前节点
*返回值：当前子树根节点
*功能：先右旋后左旋调平衡
**********************************************/
AVLTreeNode *AVLTree::RightAndLeftRotate(AVLTreeNode *tempNode)
{
	tempNode->rightChild=RightRotate(tempNode->rightChild);
	return LeftRotate(tempNode);
}

/*********************************************
*参数：待插入元素,当前节点
*返回值：当前子树根节点
*功能：插入元素到当前节点的子树
**********************************************/
AVLTreeNode *AVLTree::Insert(int tempKey,AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return tempNode=new AVLTreeNode(tempKey);
	else 
	{
		if(tempKey==tempNode->key)
			return tempNode;
		else if(tempKeykey)
			tempNode->leftChild=Insert(tempKey,tempNode->leftChild);
		else tempNode->rightChild=Insert(tempKey,tempNode->rightChild);
	}
	//tempNode->height=max(GetHeight(tempNode->leftChild),GetHeight(tempNode->rightChild))+1;
	if(2==GetHeight(tempNode->leftChild)-GetHeight(tempNode->rightChild))
	{
		if(tempKeyleftChild->key)
			tempNode=RightRotate(tempNode);
		else tempNode=LeftAndRightRotate(tempNode);
	}
	else if(-2==GetHeight(tempNode->leftChild)-GetHeight(tempNode->rightChild))
	{
		if(tempKey>tempNode->rightChild->key)
			tempNode=LeftRotate(tempNode);
		else tempNode=RightAndLeftRotate(tempNode);
	}
	tempNode->height=max(GetHeight(tempNode->leftChild),GetHeight(tempNode->rightChild))+1;
	return tempNode;
}
void AVLTree::Insert(int tempKey)
{
	root=Insert(tempKey,root);
}

/*********************************************
*参数：待删除元素,当前节点
*返回值：当前子树根节点
*功能：删除元素
**********************************************/
AVLTreeNode *AVLTree::Delete(bool &isDelSucceed,int tempKey,AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return NULL;
	else 
	{
		if(tempKey==tempNode->key)
		{
			if(NULL==tempNode->rightChild)
			{
				AVLTreeNode *cur=tempNode;
				tempNode=tempNode->leftChild;
				delete cur;
				isDelSucceed=true;
				return tempNode;
			}
			else//找到右子树最小的元素代替，然后删除 
			{
				AVLTreeNode *cur=tempNode->rightChild;
				while(cur->leftChild!=NULL)
					cur=cur->leftChild;
				tempNode->key=cur->key;
				tempNode->rightChild=Delete(isDelSucceed,cur->key,tempNode->rightChild);
			}
		}
		else if(tempKeykey)
			tempNode->leftChild=Delete(isDelSucceed,tempKey,tempNode->leftChild);
		else tempNode->rightChild=Delete(isDelSucceed,tempKey,tempNode->rightChild);
		
		if(-2==GetHeight(tempNode->leftChild)-GetHeight(tempNode->rightChild))//删除的是左子树上的
		{
			if(GetHeight(tempNode->rightChild->rightChild)>=GetHeight(tempNode->rightChild->leftChild))
				tempNode=LeftRotate(tempNode);
			else tempNode=RightAndLeftRotate(tempNode);
		}
		else if(2==GetHeight(tempNode->leftChild)-GetHeight(tempNode->rightChild))
		{
			if(GetHeight(tempNode->leftChild->leftChild)>=GetHeight(tempNode->leftChild->rightChild))
				tempNode=RightRotate(tempNode);
			else tempNode=LeftAndRightRotate(tempNode);
		}
		tempNode->height=max(GetHeight(tempNode->leftChild),GetHeight(tempNode->rightChild))+1;
	}
	return tempNode;
}
bool AVLTree::Delete(int tempKey)
{
	bool isDelSucceed=false;
	root=Delete(isDelSucceed,tempKey,root);
	return isDelSucceed;
}

/**********************************************************
*参数：待修改节点元素、修改后的元素
*返回值：返回修改是否成功
*功能：修改函数
************************************************************/
bool AVLTree::Updata(int oldKey,int newKey)
{
	if(Delete(oldKey))
	{
		Insert(newKey);
		return true;
	}
	return false;
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：前序遍历二叉查找树
************************************************************/
void AVLTree::PreOrderPrint(AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return ;
	coutkeyleftChild);
	PreOrderPrint(tempNode->rightChild);
}
void AVLTree::PreOrderPrint()
{
	PreOrderPrint(this->root);
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：中序遍历二叉查找树
************************************************************/
void AVLTree::InOrderPrint(AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return ;
	InOrderPrint(tempNode->leftChild);
	coutkeyrightChild);
}
void AVLTree::InOrderPrint()
{
	InOrderPrint(root);
}

/**********************************************************
*参数：当前子树根节点
*返回值：空
*功能：后序遍历二叉查找树树
************************************************************/
void AVLTree::SufOrderPrint(AVLTreeNode *tempNode)
{
	if(NULL==tempNode)
		return ;
	SufOrderPrint(tempNode->leftChild);
	SufOrderPrint(tempNode->rightChild);
	coutkeyleftChild,tempColumn+1);
	for(int i=0;ikeyrightChild,tempColumn+1);
}
void AVLTree::RotatePrint()
{
	RotatePrint(root,0);
}

void Menu()
{
	int val,choice,newVal;
	AVLTree myAVLTree;
	while(true)
	{
		do
		{
			cout>choice; 
		}while(choice!=1&&choice!=2&&choice!=3&&choice!=4&&choice!=5&&choice!=6);
		if(1==choice)
		{
			cin>>val;
			myAVLTree.Insert(val);
		}
		else if(2==choice)
		{
			cin>>val;
			if(myAVLTree.Delete(val))
				cout>val>>newVal;
			if(myAVLTree.Updata(val,newVal))
				cout>val;
			if(NULL!=myAVLTree.Search(val))
				cout
 
      上面是我的源代码，可能有很多不合理的地方，欢迎斧正！
 
 
 
 
时序图与状态图（Rose） - Windows XP经典软件系列,搜素材,soscw.com
时序图与状态图（Rose） - Windows XP经典软件系列
标签：avl树   平衡二叉查找树   
原文地址：http://blog.csdn.net/xiaobin_hlj80/article/details/24584281